Этих трех элементов логических функций и операций переноса(сдвига) достаточно, для тог, чтобы организовать любую операцию арифметического вычисления или сравнения чисел в двоичной системе счисления.
Под сдвигом понимается смещение разрядов двоичного числа в право или в лево, в зависимости от указанного направления. Освободившееся после сдвига место заполняется нулями. В любой позиционной системе счисления сдвиг в лево(<<) на один разряд означает умножение на основание системы счисления, а сдвиг в право(>>) на один разряд - деление на основание системы счисление.
Пример 1.
Дано A(10)=123. Умножить число с помощью операции сдвига на 100(10).
Решение:
100=102 следовательно для умножения заданного числа на 100 необходимо выполнить сдвиг на два разряда в лево
A(10)=123*100=123 << 2=12300
Ответ A(10)=12300.
Пример 2.
Дано A(10)=345. Разделить число с помощью операции сдвига на 1000(10).
Решение:
Для выполнения операции деления на 1000 необходимо умножить исходное число на 1/1000
1/1000=0,001=10-3 следовательно для деления заданного числа на 1000 необходимо выполнить сдвиг на три разряда в право
A(10)=345/1000=345 >> 3=0,345
Ответ A(10)=0,345.
Пример 3.
Дано A(2)=11010. Умножить число с помощью операции сдвига на 100(2).
Решение:
100=22 следовательно для умножения заданного числа на 100 необходимо выполнить сдвиг на два разряда в лево
A(10)= 11010*100=11010 << 2=1101000
Ответ A(2)= 1101000.
Пример 4.
Дано A(2)=11010. Разделить число с помощью операции сдвига на 10 (2).
Решение:
Для выполнения операции деления на 10 необходимо умножить исходное число на 1/10
1/10=0,1=10-1 следовательно для деления заданного числа на 10 необходимо выполнить сдвиг на один разряда в право
A(10)=11010/10=11010 >> 1=1101
Ответ A(2)=1101.
Поскольку двоичная система счисления состоит всего из двух чисел {0,1} принято считать, что 0(2) в логических функциях представляет собой лож, а 1(2) истину. Исходя из этого при помощи логических элементов можно организовать любой вычислительный процесс. Рассмотрим процесс сложения двоичных чисел на примере двухразрядного сумматора рисунок 9.
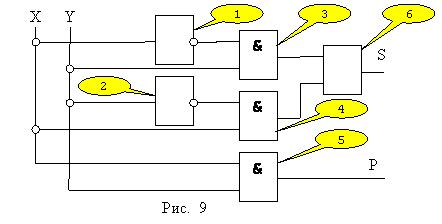
Для понимания принципа использования логических функций построим таблицу истинности получающуюся при выполнении процесса сложения для всех элементов таблица 13.
Таблица 13. Процессы происходящие в двухразрядном сумматоре.
|
X |
Y |
1 (не X) |
2 (не Y) |
3 (Y и 1) |
4 (X и 2) |
5 (XиY) |
6 (3или4) |
S |
P |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.