Алгоритм поразрядного перевода из двоичной системы счисления в восьмеричную заключается в дроблении двоичного числа по три разряда с права на лево и замене соответствующими цифрами восьмеричной системы счисления из таблицы 4. Если в конце дробления остается меньше трех разрядов, то двоичное число дополняют с лева нулями. Алгоритм перевода представлен на рисунке 8.
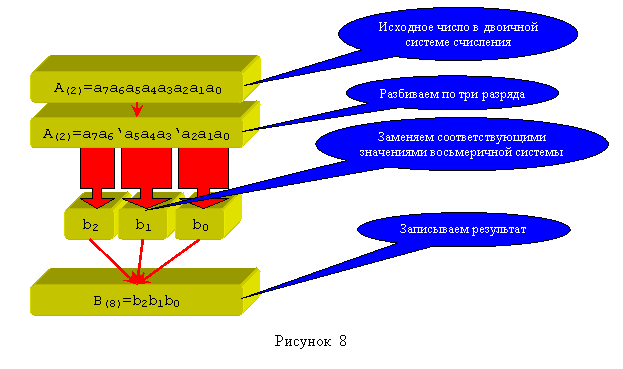
Обратный перевод из восьмеричной в двоичную систему счисления осуществляется по этому же алгоритму но в обратном порядке. Один разряд восьмеричной системы счисления заменяется тремя разрядами двоичной систем счисления.
Алгоритм перевода из двоичной в шестнадцатеричную систему счисления аналогичен алгоритму перевода в восьмеричную, за исключением того, что число дробиться не по три, а по четыре разряда и соответствия подбираются из таблицы 5.
Пример 1.
Дано A(2)=1001101. Найти A(8).
Решение:
![]()
Ответ:
A(8)=115
Пример 2.
Дано A(8)=27. Найти A(2).
Решение:
A(8)=2’7
Ответ:
A(2)=010111=10111
Пример 3.
Дано A(2)=1101101. Найти A(16).
Решение:
![]()
Ответ:
A(16)=6D
Пример 2.
Дано A(16)=F4. Найти A(2).
Решение:
A(16)=F’4
Ответ:
A(2)=11110100
3.4.4. Представление вещественных чисел в двоичной системе счисления.
В современной вычислительной технике используется два способа представления вещественных чисел в двоичной системе счисления: с фиксированной запятой и с плавающей запятой.
3.4.4.1.Представление вещественных чисел в двоичной системе счисления с фиксированной запятой.
При представлении вещественных чисел в двоичной системе счисления с фиксированной запятой форма записи остается аналогичной десятичной системе счисления XXXX,XXXX. Перевод из десятичной системы счисления осуществляется по очереди: сначала переводиться целая часть, а потом дробная.
Пример 1.
Дано A(10)=43,97. Найти A(2).
Решение:
Сначала переводим целую часть B(10)=43
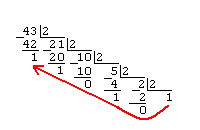
B(2)=101011
Затем дробную C(10)=97
C(2)= 1100001
Записываем результат
A(2)= 101011,1100001
К преимуществам представления вещественных чисел с фиксированной запятой относиться простота арифметических операций, а к недостаткам слишком узкий диапазон представления чисел.
3.4.4.2.Представление вещественных чисел в двоичной системе счисления с плавающей запятой.
При представлении вещественных чисел в любой системе счисления используют запись с плавающей точкой. Любое число в любой системе счисления можно предстваит в виде:
![]() ,
,
где:
Q – основание системы счисления;
A – мантисса;
p – порядок.
Например в десятичной системе счисления число 3,14 можно представить в виде:
3,14=0,314*101
Здесь мантисса равна 0,314, а порядок равен 1.
Такое представление чисел далеко не однозначно. Число 3,14 можно представить как:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.