Основы алгоритмизации и вычислений: Учебно-практическое пособие, страница 6

            N-ричная система имеет N цифр, от 0 до N-1. Формула разложении по степеням для N-ричной системы счисления будет иметь следующий вид:

            где:

                        - значение числа в N-ричной системе счисления;

                        q – количество разрядов числа записанного в N-ричной системе счисления.

                        i – номер разряда;

                        - значение i-го разряда числа записанного в N-ричной системе счисления.

                        N – основание системы счисления, в которой записано число.

            Примером N-ричной системы счисления может служить троичная, четверичная и т.д.

3.3. Системы счисления, используемые в вычислительной технике.

            Ввод и вывод информации при работе с вычислительной техникой происходит в привычной для человека десятичной системой счисления. Однако все операции по обработке и хранению данных любое устройство вычислительной техники выполняет в двоичной системе счисления. Кроме того в устройствах вычислительной техники используются вспомогательные системы счисления: это восьмеричная (система счисления по основанию 8) и шестнадцатеричная – система счисления по основанию 16.

3.3.4.  Двоичная система счисления.

            Основание двоичной системы счисления равно 2 (p=2) определяет число цифр входящих в данную систему счисления: {0,1} две цифры. Двоичная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в двоичной системе счисления имеет следующий вид:

            где:

                        - значение числа в двоичной системе счисления;

                        q – количество разрядов числа записанного в двоичной системе счисления.

                        I – номер разряда;

                        - значение i-го разряда числа записанного в двоичной системе счисления.

            Так для четырехразрядного числа, записанного в двоичной системе счисления формула разложения по степени основания будет иметь следующий вид:

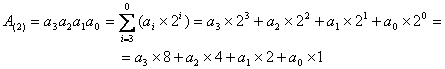
3.3.2. Восьмеричная система счисления.

            Основание восьмеричной системы счисления равно 8 (p=8) определяет число цифр входящих в данную систему счисления: {0,1,2,3,4,5,6,7} восемь цифр. Восьмеричная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в восьмеричной системе счисления имеет следующий вид:

            где:

                        - значение числа в восьмеричной системе счисления;

                        q – количество разрядов числа записанного в восьмеричной системе счисления.

                        I – номер разряда;

                        - значение i-го разряда числа записанного в восьмеричной системе счисления.

            Так для четырехразрядного числа, записанного в двоичной системе счисления формула разложения по степени основания будет иметь следующий вид:

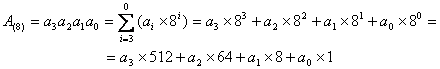
3.3.3. Восьмеричная система счисления.

            Основание шестнадцатеричной системы счисления равно 16 (p=16) определяет число цифр входящих в данную систему счисления: {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} шестнадцать цифр. Поскольку в алфавит шестнадцатеричной системы счисления входит больше дести цифр, определенных для десятичной системы счисления, остальные цифры обозначаются буквами латинского алфавита.  Шестнадцатеричная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в шестнадцатеричной системе счисления имеет следующий вид: