Основы алгоритмизации и вычислений: Учебно-практическое пособие, страница 5

Пример 1.

            Подсчитаем объем памяти, требуемый для хранения книги объемом 100 страниц, при учете, что в среднем на каждой странице по 40 строк, а в каждой строке в среднем по 60 символов.

ü  Определяем количество символов находящихся в книге:

ü  При условии, что символ занимает 1 байт памяти для хранения книги потребуется 240000 байт памяти или

3. Системы счисления.

            Любую информацию окружающего нас мира можно представить в виде числовых значений, характеризующих положение свойства объекта относительно какой либо нулевой отметки. Совокупность способов построения, записи и наименования чисел называют системой счисления.

            История развития способов счета насчитывает многие тысячелетия. Менялись средства счета: пальцы, камешки, счеты, арифмометры, компьютеры. Но их назначение оставалось неизменным: определение качественных и количественных характеристик объектов.

            Различают два вида систем счисления это: позиционная система и непозиционная система.

Позиционная система счисления – количество определяемое цифрой числа зависит от позиции этой цифры в записи числа. Например в записи десятичной системы счисления  одна и та же цифра 1 определяет различные количества: сто, десять и один.

Непозиционная система счисления – количество определяемое цифрой числа не зависит от ее позиции. К непозиционным системам относиться римская система счисления. Например число XXX – означает тридцать, а каждый символ означает десть, то есть X+X+X=XXX.

3.1. Десятичная система счисления.

            Наиболее широко известной и применяемой на практике системой счисления является десятичная. Это позиционная система счисления. Десятичная система счисления имеет десять цифр {0,1,2,3,4,5,6,7,8,9}, что и определило название системы и ее важнейшую характеристику – основание системы. Обозначим ее буквой p. Для десятичной системы счисления p=10.

            Любую позиционную систему счисления можно разложить по степеням основания. Пусть в десятичной системе счисления задано некоторое число . Каждая позиция занимаемая цифрами называется разрядом числа. Разряды имеют названия и номера: разряд единиц, разряд десятков, разряд сотен, разряд тысяч и т.д. Названия разрядов определяют их вес: единицы, десятки, сотни, тысячи и т.д. Вес разряда равен степени основания в порядке номера разряда.

В общем случае для разложения по степеням основания числа, записанного в десятичной системе счисления выражение будет иметь следующий вид:

(2)

            где:

                        n – количество разрядов числа;

                         - значение соответствующего разряда.

                                   где i – вес соответствующего разряда.

            Так при разложения в степенной ряд по основанию десятичного числа  получим:

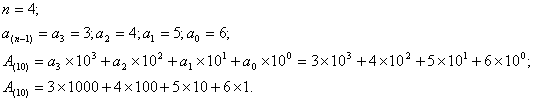
            Последняя запись представляет собой сумму произведений цифр числа на вес разрядов. Эту запись называют формулой разложения числа.

3.2. N-ричная система счисления.

            Десятичная система счисления является частным случаем N-ричной системой счисления, то есть  системой счисления по основанию N. p=N, где N – положительное целое число.