Примеры расчета деревянных конструкций: Учебное пособие по дисциплине «Конструкции из дерева и пластмасс», страница 4

         Отсюда видно, что недонапряжение значительное. Однако, можно убедиться, что если для верхней обшивки принять листы толщиной 8 мм (вместо 10 мм в данном примере), то они не будут удовлетворять прочности от действия сосредоточенной силы P=1000 Н.

Проверяем прочность нижней растянутой обшивки:

,

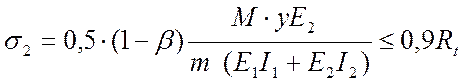где    R_t – расчетное сопротивление листового асбестоцемента растяжению;

 –  расстояние от наиболее удаленной точки сечения до нейтральной оси.

Т. к. модули упругости равны Е₁=Е₂, то:

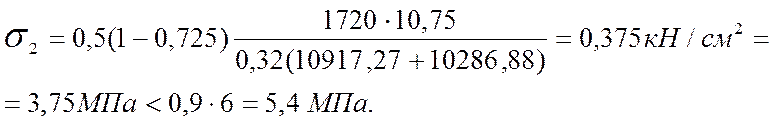
         Очевидно, для нижней растянутой обшивки можно использовать листы с минимальной толщиной 6 мм в силу запаса прочности более чем в 2 раза. Этот вариант предоставляется проверить самостоятельно. Однако лист с толщиной 6 мм целесообразно рекомендовать для ненагруженных конструкций, например, подвесных потолков.

         3. Расчет ребер каркаса.

Нормальные напряжения в ребрах каркаса:

 _,

 

где    R_u– расчетное сопротивление древесины изгибу;

 –  расстояние от наиболее удаленной точки сечения до нейтральной оси.

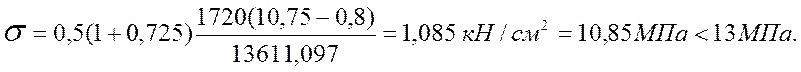
         Учитывая значительное недонапряжение, целесообразно рекомендовать уменьшенное сечение бруса, ближайшее по сортаменту с учетом острожки 55x170 мм.        

Касательные напряжения в ребрах каркаса:

_,

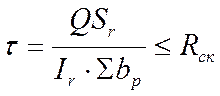где    R_ск– расчетное сопротивление древесины скалыванию,      R_ск=1,6 МПа;

S_r – статический момент сдвигаемой части поперечного сечения плиты;

         ∑ b_p– суммарная ширина ребер каркаса;

I_r– приведенный (к материалу каркаса) момент инерции.

         Вычислим статический момент сдвигаемой части поперечного сечения плиты относительно нейтральной оси:

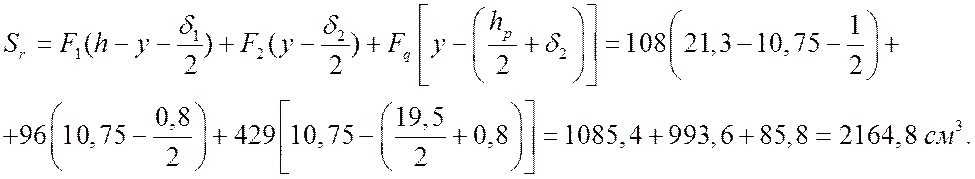
Приведенный момент инерции сечения плиты:

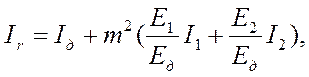
 или при Е_д=Е_а :

,

Суммарная ширина ребер каркаса составляет:

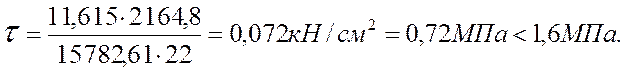
         4. Расчет соединений обшивок с каркасом.

         Расчетное усилие T_s, которое может быть воспринято одним элементом соединения, определяется из следующих условий:

а) смятие древесины каркаса

,

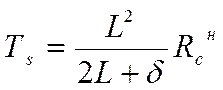где    δ – толщина обшивки;

R_c^н = 13 МПа –  сопротивление древесины 2 сорта смятию [1];

,

 

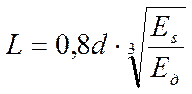где    E_s – модуль упругости материала элемента соединения;

d– диаметр элемента соединения.

В качестве крепежных элементов используем оцинкованные стальные шурупы диаметром d=5 мм и длиной 40 мм с потайной головкой:

 

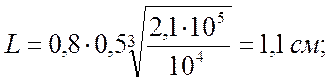
расчетное усилие, которое может быть воспринято одним элементом соединения:

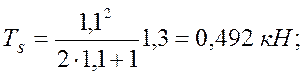
б) смятие асбестоцементных обшивок

,

где    R_р – расчетное сопротивление листового асбестоцемента смятию;

T_s = = 0,486кН;

в) срез элемента соединения

,

где    R_bs – расчетное сопротивление материала элемента соединения срезу,

T_s = = 2,944 кН.

В расчет принимаем наименьшее значение, т.е. T_s = 0,486 кгс.

Проверку соединения обшивок с каркасом производят по условию:

,

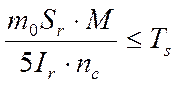где    Т_s – наименьшее из трех полученных ранее значений;

         n_с – число принимаемых срезов элементов соединения в каждом шве на рассматриваемом участке с однозначной эпюрой поперечных сил,

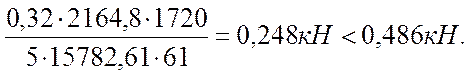
5. Расчет прогибов.

         При расчете асбестоцементных плит по предельным состояниям второй группы определяют максимальный относительный прогиб плиты по формуле:

_;

 

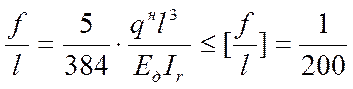где     – максимальный относительный прогиб балки, определяемый по таб. 19, СНиП 2.01.07-85.

что в пределах допустимого.

Прогибы асбестоцементных обшивок каркасных плит проверяют по формуле:

,

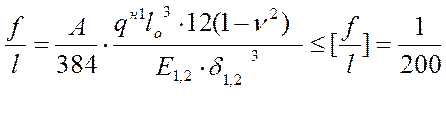где    ν = 0,2 – коэффициент поперечной деформации асбестоцемента (коэффициент Пуассона);

         l_o – расстояние между продольными ребрами (рисунок 1);

A– зависит от количества продольных прогонов.

Проверяем прогибы асбестоцементных обшивок

- в верхней обшивке:

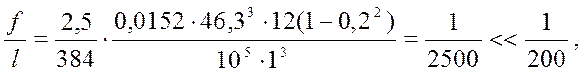
где    q^н1 – нормативная нагрузка, воспринимаемая асбоцементной верхней обшивкой, q^н1 = 0,09+0,175+1,26 = 1,525кН/м²; при ширине полосы в 1 см – q^н1 = = 0,0152 кН/м;

          – коэффициент максимального прогиба в крайнем пролете трехпролетной балки (по числу шагов между продольными ребрами).