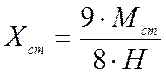 ;
;
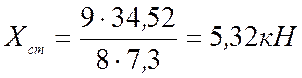 .
.
Анализируя
результаты статического расчета рамы, можно сделать вывод о том, что опасным
сечением, в котором возникают максимальные сила N, изгибающий
момент M и поперечная
сила Q является
сечение 1-1 на уровне обреза фундамента (в заделке). Для определения усилий в
опасном сечении, из двухшарнирной рамы вырезаем стойку, к ней прикладываем
местную нагрузку, действие отброшенных связей заменяем соответствующими
реакциями. Определение внутренних силовых факторов M, N, Q ведем как для
консольной балки. Расчетные усилия от кратковременных нагрузок принимаем с
коэффициентом сочетания ![]() .
.
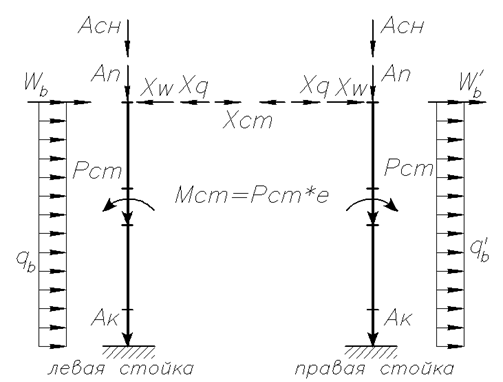
Рисунок 72. Расчетная схема двухшарнирной рамы для определения усилий в стойке
Усилия определяем для левой и правой стоек.
Максимальные усилия возникают в нижнем сечении колонн у заделки в фундамент. Изгибающие моменты в левой и правой стойке определяются из выражения:
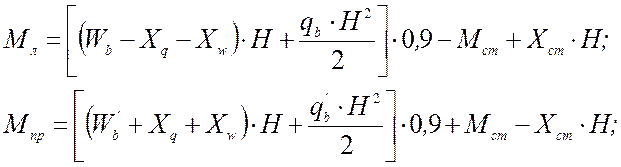
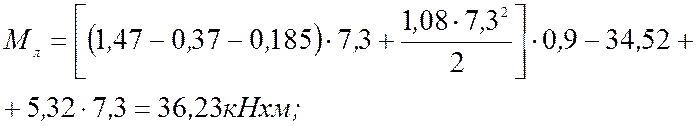
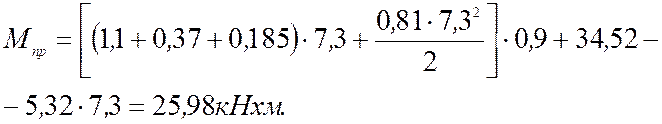
Поперечные силы в стойках:
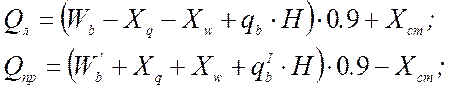
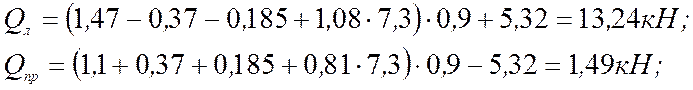
Продольное усилие сжатия:
![]() ,
, ![]()
2 Расчет клееной стойки
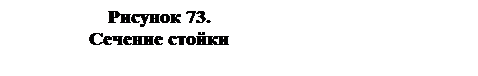
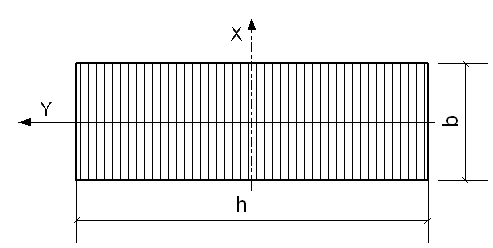 Определив усилия
M, N, Q в опасном
сечении стойки, переходим к подбору сечения стойки. Предварительно, на
основании опыта проектирования подобных элементов, задаемся сечением стойки.
Высота стойки определена ориентировочно
Определив усилия
M, N, Q в опасном
сечении стойки, переходим к подбору сечения стойки. Предварительно, на
основании опыта проектирования подобных элементов, задаемся сечением стойки.
Высота стойки определена ориентировочно 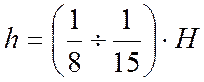 =0,73м,
ширина стойки
=0,73м,
ширина стойки 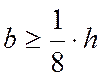 =0,15м. Сечение
стойки развито в плоскости рамы. Набирается сечение стойки из досок плашмя.
Толщина доски не более 40 мм, после двухсторонней острожки толщина доски
=0,15м. Сечение
стойки развито в плоскости рамы. Набирается сечение стойки из досок плашмя.
Толщина доски не более 40 мм, после двухсторонней острожки толщина доски ![]() . Высота сечения стойки уточняется
соответственно с толщиной доски h=0,726м. Влажность клееной древесины
должна быть не более
. Высота сечения стойки уточняется
соответственно с толщиной доски h=0,726м. Влажность клееной древесины
должна быть не более ![]() . Для принятого сечения стойки
определяется геометрические характеристики сечения и гибкость
. Для принятого сечения стойки
определяется геометрические характеристики сечения и гибкость ![]() и
и ![]() .
.
Площадь сечения
![]() .
.
Моменты сопротивления:
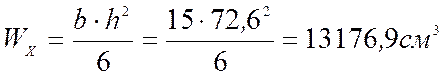 ;
;
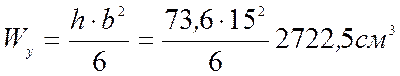 ;
;
Моменты инерции:
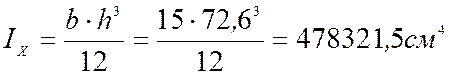 ;
; 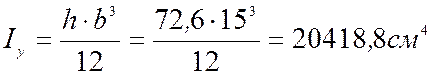 ;
;
Гибкость стойки относительно оси X определяется из выражения:
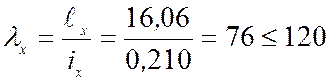 ,
,
где ![]() - расчетная длина стойки,
- расчетная длина стойки, ![]() , при жестком защемлении в фундаменте
, при жестком защемлении в фундаменте
![]() - радиус инерции для прямоугольного
сечения, равен
- радиус инерции для прямоугольного
сечения, равен ![]() .
.
Гибкость должна
быть не более ![]()
При большей гибкости необходимо изменить размеры поперечного сечения стойки.
Гибкость стойки относительно оси Y будет равна:
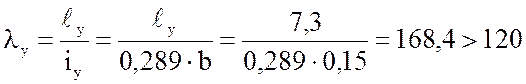 ,
,
где ![]() -
расчетная длина стойки относительно оси Y, которая
зависит от наличия связей и распора по стойкам. Относительно оси Y гибкость также
не должна превышать предельного значения
-
расчетная длина стойки относительно оси Y, которая
зависит от наличия связей и распора по стойкам. Относительно оси Y гибкость также
не должна превышать предельного значения ![]() . Предварительно принимаем
. Предварительно принимаем ![]() – это расстояние между узлами закрепления стойки.
– это расстояние между узлами закрепления стойки.
Поскольку гибкость превышает предельно допустимую, необходимо ввести распорки.
Тогда расчетная
длина из плоскости будет равна расстоянию между узлами
вертикальных связей, поставленных по колоннам в плоскости продольных стен ![]() .
.
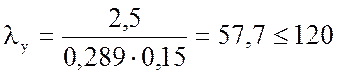
Определив геометрические характеристики сечения и усилия в колонне, выполняем проверки по прочности и устойчивости.
Проверка по устойчивости по оси Х выполняется по формуле:
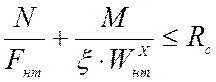 ;
;
где N, M – расчетные значения продольной силы и изгибающего момента в заделке;
Fнт – площадь сечения нетто;
![]() -
момент сопротивления нетто относительно оси X;
-
момент сопротивления нетто относительно оси X;
![]() – коэффициент, учитывающий
влияние продольного изгиба
– коэффициент, учитывающий
влияние продольного изгиба
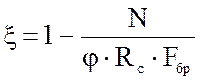 ,
,
где 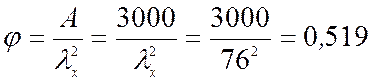 при
при ![]() .
.
![]() -
расчетное сопротивление древесины при работе на сжатие;
-
расчетное сопротивление древесины при работе на сжатие;
![]() [1 п.
3.1, табл.3];
[1 п.
3.1, табл.3];
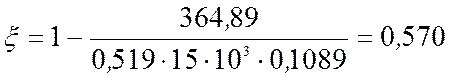 ;
;
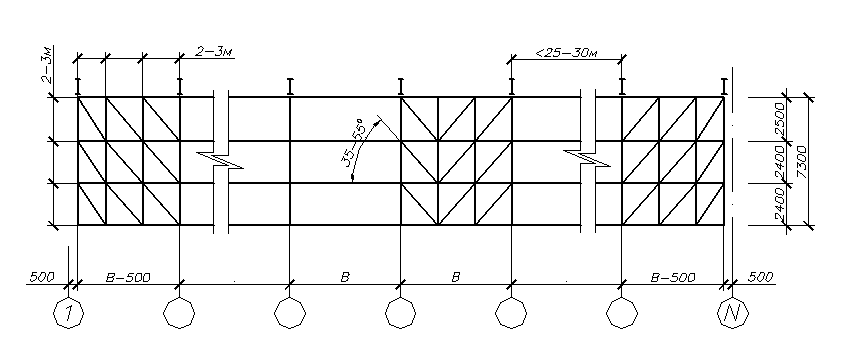
Рисунок 74. Вертикальные связи по стойкам
Проверяю устойчивость:
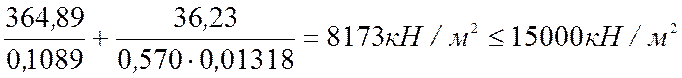 .
.
Относительно оси Y прочность стойки проверяем как центрально-сжатого элемента по формуле:
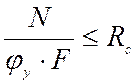
где ![]() –
коэффициент продольного изгиба определяется в зависимости от гибкости
–
коэффициент продольного изгиба определяется в зависимости от гибкости ![]() . Поскольку
. Поскольку ![]() , то
значение
, то
значение ![]() определяется по
формуле
определяется по
формуле
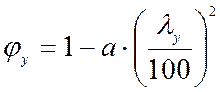 ,
,
где коэффициент а=0,8 для древесины.
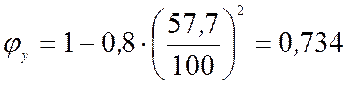 .
.
Выполняем проверку 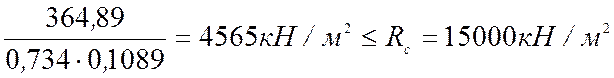 .
.
Проверка устойчивости плоской формы деформирования производится по формуле:
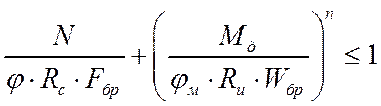 ,
,
где Fбр – площадь брутто с максимальными размерами сечения элемента на участке lу;
Wбр – максимальный момент сопротивления брутто на рассматриваемом участке lу относительно оси У;
n = 2 – для элементов без закрепления растянутой зоны из плоскости деформирования;
j =![]() –
коэффициент продольного изгиба, определяемый для гибкости участка элемента
расчетной длиной lу из плоскости деформирования;
–
коэффициент продольного изгиба, определяемый для гибкости участка элемента
расчетной длиной lу из плоскости деформирования;
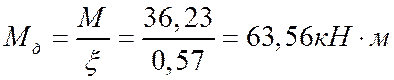 ;
;
jм – коэффициент,
определяемый по формуле 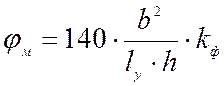 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.