Примеры расчета деревянных конструкций: Учебное пособие по дисциплине «Конструкции из дерева и пластмасс», страница 27

 Вычисляем прочность поперечного сечения:

<.

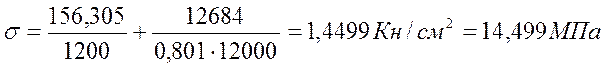Для обеспечения устойчивости плоской формы деформирования арки, закрепляем к ней плиты шириной 150 см и ставим скатные связи, прикрепляемые к верхним кромкам арок, через см.

Проверяем устойчивость полуарки с положительным моментом и раскрепленной сжатой кромкой, согласно СНиП II-25-80 п.4.18.

М_расч.=12684 кН∙см, N_соотв=156,305 кН /см².

,

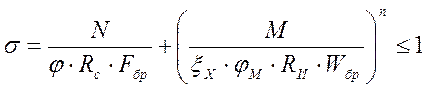где

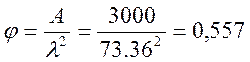 - коэффициент продольного изгиба;

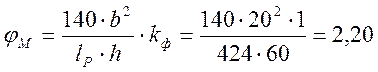
где: F_бр – площадь брутто с максимальными размерами сечения элемента на участке l_p; W_бр – максимальный момент сопротивления брутто на рассматриваемом участке l_p; l_p – расстояние между опорными сечениями элемента; b – ширина поперечного сечения; h – максимальная высота поперечного сечения на участке l_p; k_ф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l_p, определяемый по СНиП II-25-80 табл. 2 прил. 4.

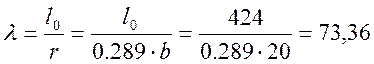 - гибкость элементов цельного сечения, где  - шаг связей; ; - для элементов, имеющих закрепление;

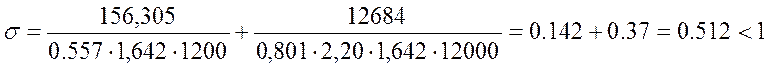
Таким образом, устойчивость плоской формы деформирования обеспечена.

Прочность поперечного сечения арки по касательным напряжениям определяем по СНиП II-25-80  п.4.27.

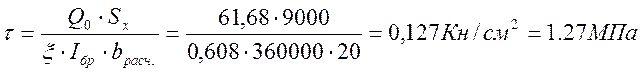 < Rск=1,425МПа, где

 - момент инерции сечения арки;

 Q₀ – расчетная максимальная поперечная сила 61,68 кН (комбинация нагрузок: ветровой и постоянной, см. приложение 1, элемент 1);

S_х=9000см³– статический момент сдвигаемой части приведенного сечения      относительно нейтральной оси, определённый выше;

– расчетное сопротивление скалыванию древесины вдоль волокон наружных слоев, где  и  - коэффициенты, определённые выше;

b_рас=20 см– расчетная ширина сечения, которую следует принимать равной суммарной ширине ребер каркаса;

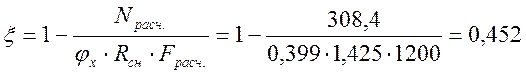- коэффициент, изменяющийся от 1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, где:

 - расчётная площадь сечения арки;

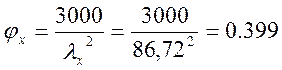 - коэффициент продольного изгиба, где коэффициент А = 3000 для древесины, принимается по СНиП II-25-80 п.4.3, где 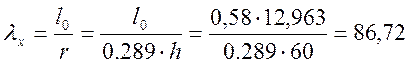 -  гибкость элементов цельного сечения, где  l_о – расчетная длина элемента; r – радиус инерции сечения элемента брутто соответственно относительно оси Х;  - расчетная длина трехшарнирной арки при несимметричной нагрузке, принимается по СНиП II-25-80 п.6.25, где  - длина дуги полуарки.

Принимаем клееный пакет из 15 досок (4·15=60см) сосны 2-го сорта.

4. Расчет стальных элементов арки

Опорный узел

Расчетные усилия в опорном узле: нормальная сила N_расч.=290,9кН (комбинация нагрузок: ветровой и постоянной, см. приложение 1, элемент 1).

а). Проверку торца на смятие выполняем по формуле:

,

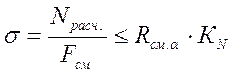где

 - площадь смятия торца, принимаемая из условия: ;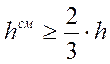

 – расчётное сопротивление древесины смятию, принимается по СНиП II-25-80 п.3.1, таб. 3;

  –коэффициент, применяемый при расчете на смятие древесины в нагельном гнезде, принимается по СНиП II-25-80 п.5.14, таб. 19;

;

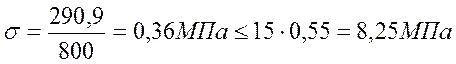Проверка торца на смятие выполняется, принимаем .

б). Арка крепится к фундаменту через уголок L200x10 l=200мм. Опорную пластину принимаем конструктивно 300х650х12мм. Задаём диаметр болтов и определяем их количество из формулы определения количества нагелей в сечении, взятой по СНиП II-25-80 п.5.13, п.5.14.

Число болтов равно: 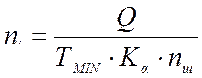, где:

     Q=18,55кН – расчетное усилие (комбинация нагрузок: ветровой и постоянной, см. приложение 1, элемент 1);

Т_min – наименьшая расчетная несущая способность, найденная по формуле:

  – несущая способность нагеля на смятие среднего элемента, где  - толщина среднего элемента;  - диаметр болта;

  n_ш=2 –  число расчетных швов одного нагеля.      

 – коэффициент, применяемый при расчете на смятие древесины при α=90⁰, принимается по СНиП II-25-80 п.5.14, таб. 19.

.

Принимаем 2 болта диаметром 16 мм.

в). Анкерные болты подбираются из условия работы болтов на смятие по СНиП II-23-81* «Стальные конструкции» п.11.7. формулы 127 и 128.

,

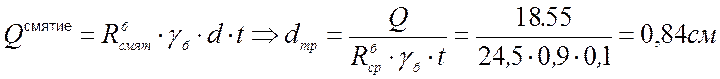где

 - сопротивление соединяемых листов стали С255;

 - коэффициент условий работы соединения, который следует принимать по СНиП II-23-81* табл. 35*, учитывая, что мы применяем болты нормальной точности;