Примеры расчета деревянных конструкций: Учебное пособие по дисциплине «Конструкции из дерева и пластмасс», страница 2

Несущими элементами плит являются продольные ребра из прямоугольных деревянных брусьев. Принимаем их высоту равной 200 мм, что соответствует 1/30 пролета; ширину ребра – 60 мм. С учетом острожки (для выравнивания поверхностей):

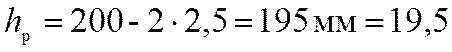см ,

.

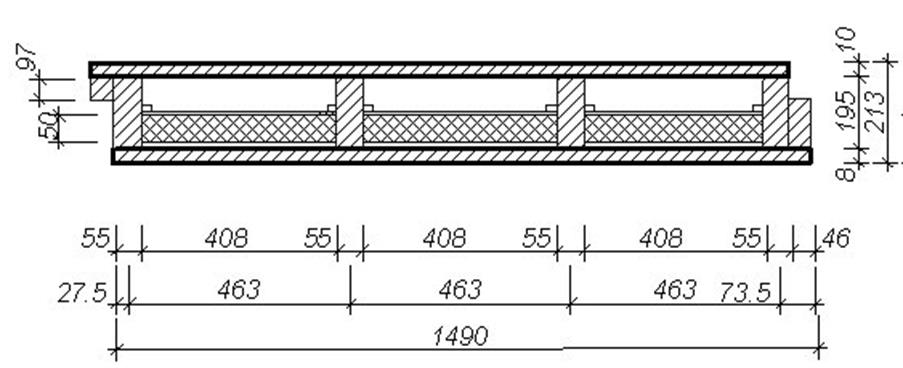
Рисунок 1.Поперечное сечение асбестоцементной плиты

         При расчете асбестоцементных каркасных плит учитывают особенность, связанную с податливостью соединений обшивок с каркасом. В этой связи при определении геометрических характеристик обшивок учитывают часть их площади поперечного сечения. Ширину сжатых обшивок принимают равной b₁=18δ₁ в каждую сторону от вертикальной оси ребра каркаса, где δ₁ – толщина верхней сжатой обшивки; ширину растянутых обшивок – соответственно b₂=25δ₂, где δ₂ – толщина растянутой обшивки (рисунок 2). Значение b₂ не должно превышать половины расстояния между ребрами каркаса.

              b                                          b   b

b b                                           b

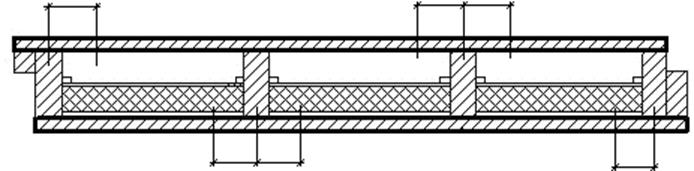
Рисунок 2. Поперечное сечение каркасной плиты

В соответствии с изложенным выше и рисунком 2 расстояние между продольными ребрами назначаем равным 463 мм, т.к.

b₂== 200 < 463/2 = 231 мм, т.е. принимаем 4 продольных ребра каркаса сечением 55х195 мм.

         2. Расчет обшивок плиты.

Поскольку в поперечном сечении плиты (рисунок 1) будет 6 участков шириной b₁ (рисунок 2), расчетную ширину верхней обшивки определим по формуле:

b_1расч=;

соответственно:

b_2расч=.

Площадь поперечного сечения:

- верхней обшивки     F₁ =δ₁ b_1расч.= = 10800 мм² = 108 см²;

- нижней обшивки      F₂ =δ₂ b_2расч==9600 мм² =96 см²;

- продольных ребер    F_д = = 42900 мм²=429 см².

         Выберем произвольную горизонтальную ось, совмещенную с нижней гранью нижней обшивки. Определим статические моменты относительно этой оси:

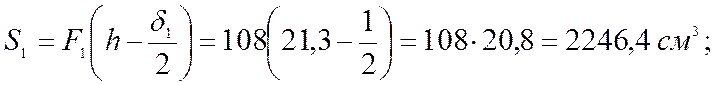
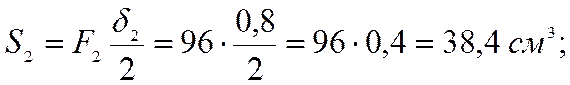
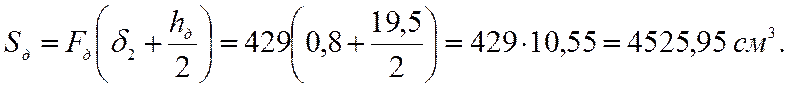
         Положение нейтральной оси сечения плиты без учета податливости соединений обшивок с каркасом определяется по формуле:

,

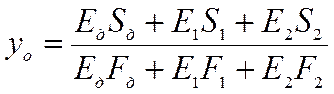где    S_д, S₁, S₂ - статические моменты деревянного каркаса, и обшивок относительно произвольной оси;

F_д, F₁, F₂ - площади поперечных сечений каркаса и обшивок.

В случае использования асбестоцементных листов с пределом прочности при изгибе равном 16 МПа , получаем Е_а=Е_д=10000 МПа.  Тогда формула примет вид:

,

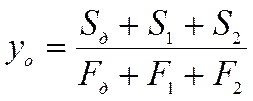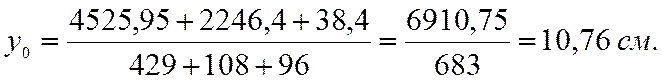
         Считаем плиту свободно опертой под равномерно распределенной нагрузкой, затем определяем коэффициент m, учитывающий распределение усилий между каркасом и обшивками по формуле:

 

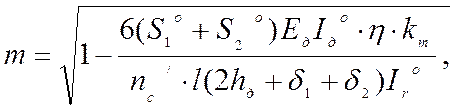
 где   S₁^o, S₂^o – приведенные (к деревянному каркасу) статические моменты обшивок (рисунок 2) относительно нейтральной оси, положение которой определяется без учета податливости соединений обшивок с каркасом;

         η – коэффициент, определяемый по СНиП 2.03.09-85 в зависимости от диаметра соединительных элементов;

k_m – коэффициент, принимаемый для элементов соединения из стали равным 1,0, из алюминия - равным 1,1;

n_c^/ – число срезов элементов соединений в каждом шве на половине пролета;

l– пролет плиты;

h_д  – высота деревянного каркаса;

I_r^о – приведенный к материалу каркаса момент инерции сечения конструкции относительно оси.

         Предварительно определим геометрические характеристики относительно оси y₀:

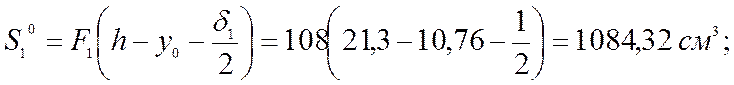
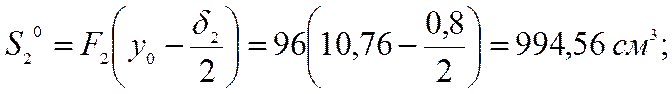
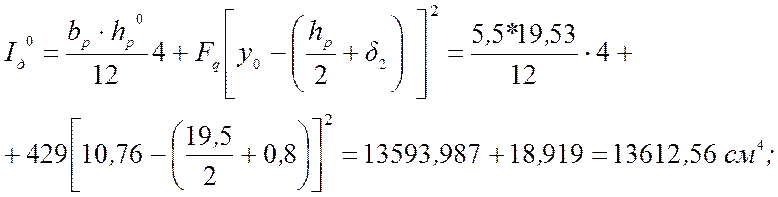
где    в соответствии с диаметром шурупов d = 0,5 см, находим

         η =  [9, черт. 3];

         K_m = 1,0 – для стальных шурупов;

         n_c^/ = 61 (количество шурупов в одном шве на половине пролета по рисунку 3.

 

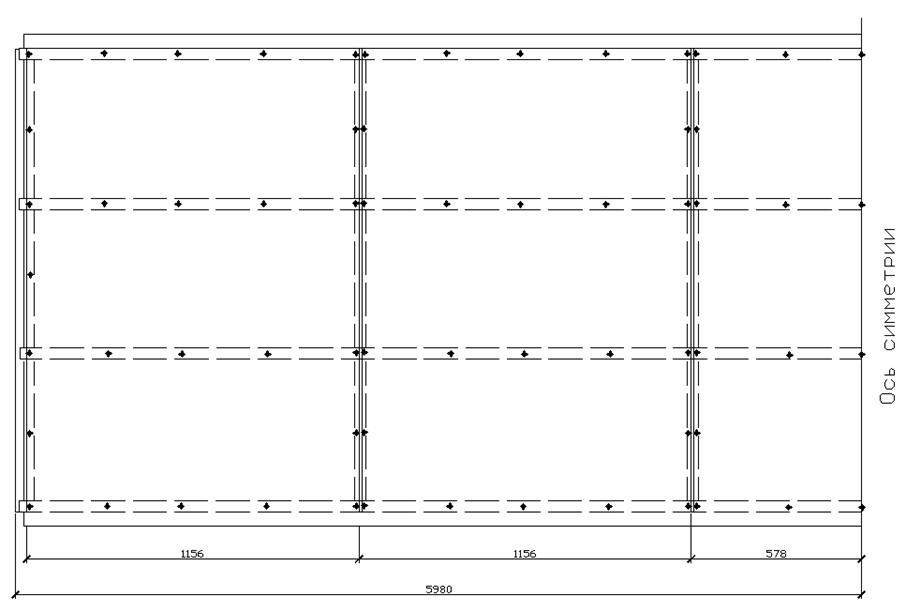Рисунок 3. Расположение элементов крепления

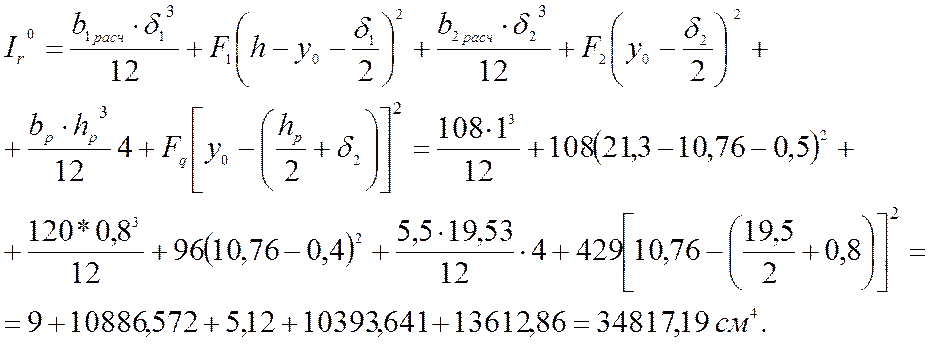
Тогда:

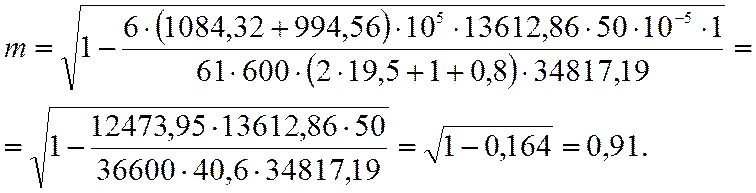
Определим положение нейтральной оси сечения плиты с учетом податливости соединений обшивок с каркасом по формуле:

,

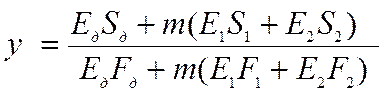с учетом условия Е_а=Е_д:

,

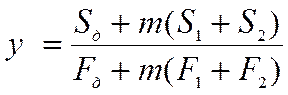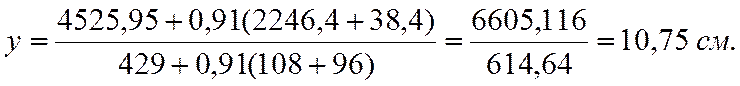
Если обе обшивки выполнены из асбестоцементных листов, то значение m_o определяется по формуле:

,

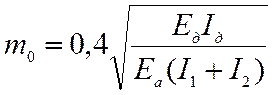где    Е_а, Е_д, I_д – соответственно модули упругости асбестоцемента, древесины и момент инерции поперечных сечений деревянных продольных ребер каркаса;