Примеры расчета деревянных конструкций: Учебное пособие по дисциплине «Конструкции из дерева и пластмасс», страница 34

При определении компонентов ветровой нагрузки w_e, следует использовать соответствующие значения аэродинамических коэффициентов: внешнего давления с_e принимаемых по обязательному приложению 4[3], где стрелками показано направление ветра. Знак «плюс» у коэффициентов с_e соответствует направ­лению давления ветра на соответствующую поверхность, знак «минус» — от поверхности. Промежуточные значения нагрузок следует определять линейной интерполяцией.

Из приложения 4 [3].

Здании с двускатными покрытиями

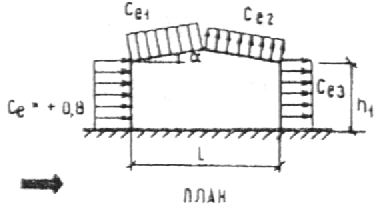
 находим при = 16° и отношении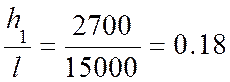   

при =0 и = 16° ; при =5 и = 16° ;

при =0.18 и = 16°

 находим при = 16° и отношении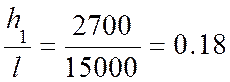   

при =0.18 и = 16°

 находим при =0.18 и отношении В/ = 43200/15000=2.88

где В=43200мм.- длина здания.

Нормативная ветровая нагрузка:

левая полурама:

на   ригеле -,

на стойке - ;

правая   полурама:

на ригеле - ;

на   стойке - .

Расчетные нагрузки.

Постоянная нагрузка:

Вес покрытия

Кратковременная нагрузка:

Снеговая нагрузка

Ветровая нагрузка:

левая полурама:

на   ригеле -,

на стойке - ;

правая   полу рама:

на ригеле - ;

на   стойке - .

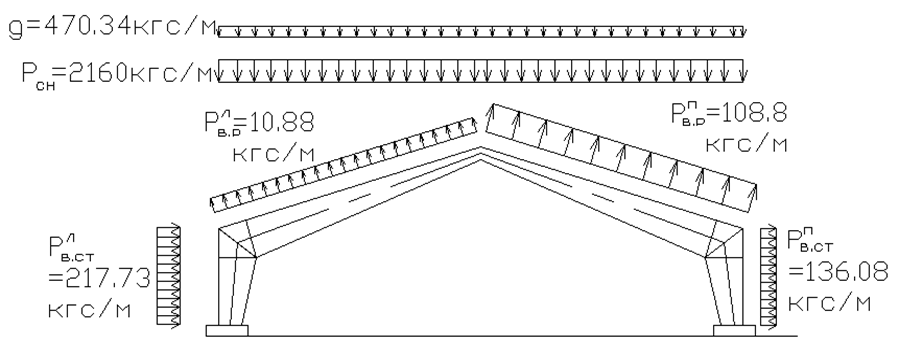
Рисунок 62. Расчетная схема

Статический расчет выполняем в программе Structure CAD. Для статического расчета учитываем модуль упругости Е =  т/м², коэффициент Пуассона μ = 0,3. Заделку опор принимаем: в правой и левой опорах – шарнирно-неподвижную. В коньковом узле вводим шарнир на одном из примыкающих к нему элементе. Постоянную и снеговую нагрузку на стержни задаем равномерно распределенной относительно общей системы координат, а ветровую относительно местной. Для выбора расчетных сочетаний усилий задаем специальные исходные данные: для собственного веса конструкций принимаем тип нагрузки – постоянная, для снеговой и ветровой – кратковременную.

3. Подбор и проверка сечений элементов рамы

Проверку сечений полурамы производим в карнизном узле, в центре которого действует максимальный изгибающий момент (элемент 30 сечение 3)

М₃₀ = -31,0255 кгс∙м   и продольная сила  N₃₀ = -21,2056 кгс.

Проверяем биссектрисное сечение a-в.

 Находим коэффициенты жесткости согласно приложению 19 по формуле схемы 6 для стойки, и по формуле схемы 7 для ригеля ([4]стр382).

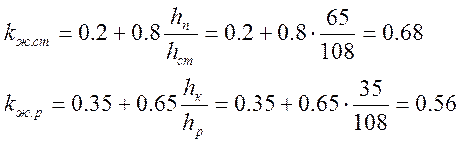
Приведенные высоты:

 для стойки 

для ригеля  

Приведенная высота сечения полурамы

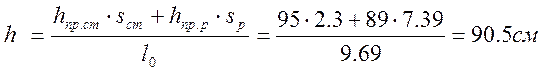
здесь длина полурамы 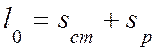= 2.3 + 7.175= 9.69м;

где s_ст и s_p—длины стойки и ригеля полурамы.

Гибкость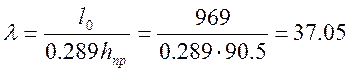 

Напряжения сжатия в биссектрисном сечении  (узел10) определяем по формуле:

Расчет на прочность внецентренно-сжатых и сжато-изгибаемых элементов следует производить по формуле (28), п. 4.17 ,[1]

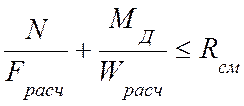 где

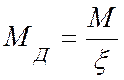
x– коэффициент, изменяющийся от 1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, определяемый по формуле ф.(30) п. 4.17 [1]

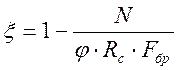
j – коэффициент, определяемый по формуле (8) п. 4.3 [1]. при гибкости элемента  l £ 70 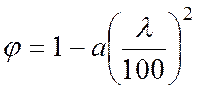; коэффициент а = 0,8 для древесины.

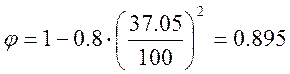
Коэффициент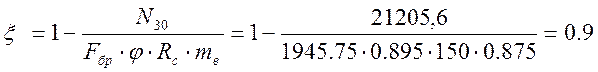

где 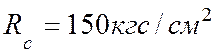([1] п 3.1, табл.3)

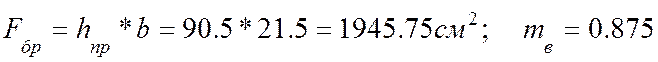        согласно([1], п. 3.2 табл.7) для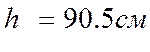

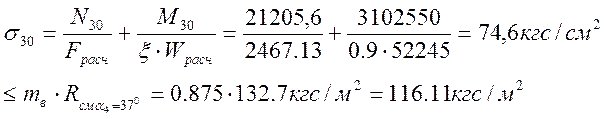
где угол смятия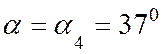

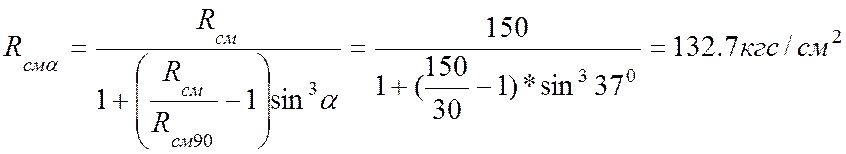([1] п.3.1 форм.1)

где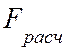- расчетная площадь;

;  ;

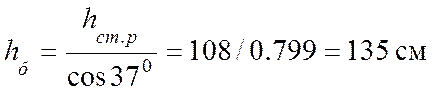расчетный момент сопротивления

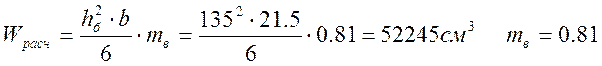— коэффициент, определяемый согласно [1], п. 3.2, табл. 7, для высоты расчетного сечения 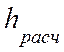= 0,85∙135 =  115 см.

Проверяем напряжения в сечении (элемент 31 сечение 3)

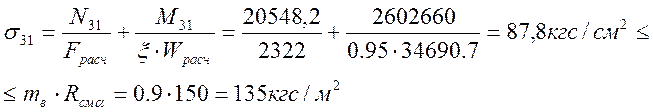
здесь, ввиду малости угла для сечения  11 (= 5).

Расчетное сопротивление древесины принимаем R_c = 150 кгс/см²;   F_pacч= 108∙21,5 = 2322 см²;

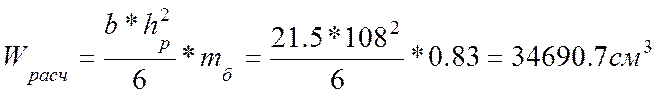
= 0,83 — коэффициент, согласно п. 3.2, табл. 7[1], для высоты расчетного сечения h_расч = 108 см.

Проверяем сечение рамы с учетом устойчивости плоской формы изгиба. При этом учитываем, что по ригелю укладываются панели по­крытия шириной 1500 мм, к стойке крепятся стеновые панели шири­ной 1200 мм. а максимальное расстояние между соединяющими их связями меньше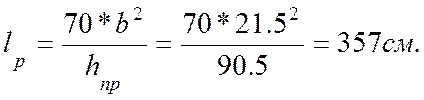

т.  е.   имеем   сплошное раскрепление растянутой кромки.

 Заменяем полураму прямолинейным сжато-изогнутым элементом переменного сечения. Длиной от пятового шарнира до точки нулевого момента в ригеле, от равномерно распределенной на всем пролете постоянной и временной нагрузок, сохранив при этом значение расчетного изгибающего момента М₃₀.