Хвилеводи. Спрямовуючі системи та спрямовані хвилі. Двоплощинний хвилевід. Порядок визначення складових поля спрямованих хвиль

 1 Хвилеводи

1.1 Спрямовуючі системи та спрямовані хвилі

Для спрямування електромагнітних хвиль від джерела до споживача використовуються спрямовуючі системи, які через цю функцію називаються хвилеводами. Наприклад, потрібно передати електромагнітну енергію від передавача до передавальної антени, чи від приймальної антени до приймача. У такому випадку такі хвилеводи називаються фідерами (від англійського слова to feed - живити). Хвилеводи бувають різними і за конструкцією і за принципом передачі (каналізації) електромагнітної енергії. На рис.1.1 зображені конструкції найбільш поширених в радіотехніці хвилеводів.

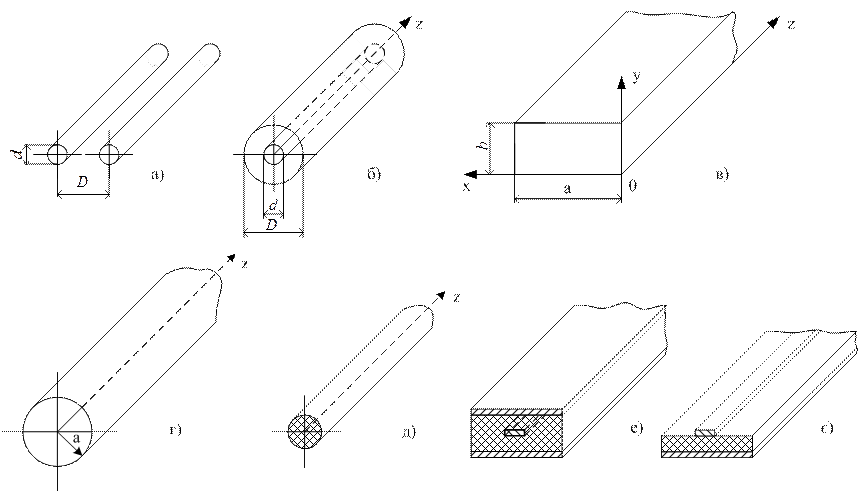
Рисунок 1.1 – Найпоширеніші хвилеводи

На рис. 1.1(а) зображено двопровідний хвилевід (двопровідна лінія передачі електромагнітної енергії), на рис. 1.1(б) – коаксіальний хвилевід (коаксіальна лінія передачі енергії), рис. 1.1(в) – прямокутний хвилевід, рис. 1.1(г) – круглий (циліндричний) хвилевід, рис. 1.1(д) діелектричний хвилевід, рис. 1.1(е) – смужковий хвилевід (симетрична смужкова лінія передачі), рис. 1.1(є) – несиметричний смужковий хвилевід (несиметрична смужкова лінія передачі енергії).

Спрямовані хвилі, що поширюються вздовж хвилеводів розділяються на поперечні, електричні, магнітні, гібридні та квазі-поперечні.

Поперечнічи хвилі Т-типу характеризуються тим, що їх поля не мають повздовжних складових, а мають лише поперечні. Такі хвилі можуть поширюватись у двопровідному та коаксіальному хвилеводах.

Електричні чи хвилі Е-типу не повинні мати повздовжньої складової вектора  і обов’язково мати повздовжню складову вектора .

Магнітнічи хвилі Н-типу не мають повздовжню складову вектора  і обов’язково мають повздовжню складову вектора .

Хвилі Е та Н типів можуть поширюватись у прямокутному, круглому та коаксіальному хвилеводах.

Гібриднимичи хвилями ЕН-типу називають хвилі, у яких є повздовжні складові і вектора , і вектора . Такі хвилі можуть поширюватись, наприклад, у діелектричному хвилеводі.

Квазі - поперечні хвилі по своїй структурі дуже близькі дохвиль Т- типу, але мають невеликі повздовжні складові векторів поля. Такі хвилі поширюються в смушкових хвилеводах.

1.2 Двоплощинний хвилевід

Розпочнемо з більш простих задач. Побудуємо картини полів, які виникають біля ідеально-провідної площини при падінні на неї у вакуумі плоскої електромагнітної хвилі. Вектори поля у хвилі, що падає на цю площину, орієнтується довільно у просторі. Але для спрощення задачі розглянемо два випадки: коли вектор  хвилі, що падає, знаходиться у площині падіння і коли цей вектор є перпендикулярним до площини падіння. Очевидно, будь – яке інше положення цього вектора можна представити як суперпозицію цих двох випадків.

Випадок перший. Вектор лежить у площині падіння (рис. 1.2.1)

Плоска хвиля падає на ідеально-провідну площину у напрямку вектора Пойнтінга . Фазові фронти цієї хвилі (площини рівних фаз) будуть перпендикулярними до вектора . На рисунку показані сліди цих фазових фронтів (суцільні лінії), які за фазами відрізняються від сусідніх на 180˚, тобто найкоротша відстань між ними дорівнює половині довжини хвилі . Тому у сусідніх фазових фронтах хвилі, що падає, вектори  та вектори  будуть мати протилежні напрямки. Причому, скрізь, вектори  знаходяться у площинах фазових фронтів (у площині рисунка) і позначаються стрілочками відповідних напрямків, а вектори  - перпендикулярними до площини рисунка, позначеними значком  (спрямовані до нас) та  (спрямовані від нас). Взаємне розташування векторів ,  та  у кожній точці рисунка відповідає формулі .

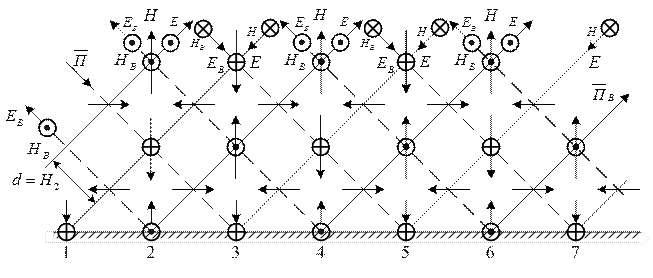
Рисунок 1.2.1

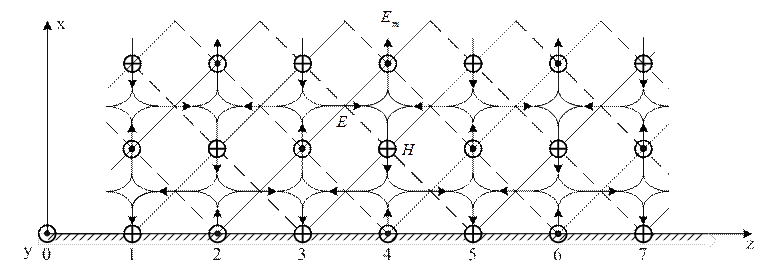
Рисунок 1.2.2

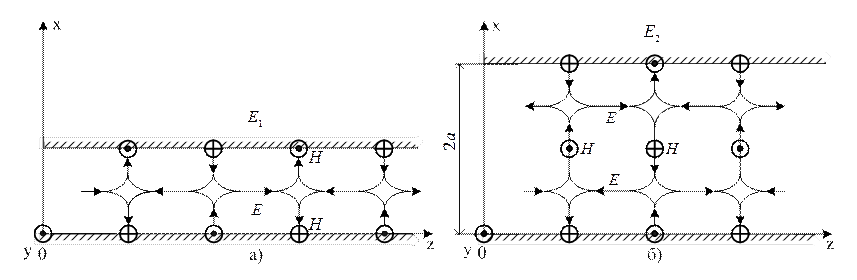
Рисунок 1.2.3

Штриховими лініями позначені сліди фронтів відбитої хвилі, яка спрямована у напрямку вектора Пойнтінга  відбитої хвилі. На цих лініях (відстань між якими теж дорівнює ) показане розташування векторів  та  відбитої хвилі, де також мається відповідність формулі . Враховуючи останню формулу і той факт, що вектор  має бути скрізь перпендикулярним до площини рисунка, покажемо його напрямок, наприклад, у точці 3. Для цього згадаємо граничні умови для тангенціальної складової вектора  на ідеально – провідній поверхні:  у нашому випадку складова вектора  складається з двох векторів:  - тангенціальної складової хвилі, що падає та тангенціальної складової відбитої хвилі. Оскільки коефіцієнт відбиття дорівнює одиниці, то . Тобто у цій точці обидва вектори будуть спрямовані в один бік (уданому випадку від нас). Очевидно в усьому фронті відбитої хвилі, якому належить т. 3, вектор  буде спрямованим так само. Напрямок вектора  у цьому фронті легко знайти з умови . В будь-яких сусідніх фронтах відбитої хвилі вектори  та  будуть мати протилежні напрямки, причому вектори  скрізь лежатимуть у площині рисунка.

Напрямки результуючих векторів  та  в усіх перехрестях фронтів визначається як векторні суми  та , бо це результуюче поле над ідеально – провідною поверхньою є результатом інтерференції хвилі, що падає та відбитої хвилі.