Хвилеводи. Спрямовуючі системи та спрямовані хвилі. Двоплощинний хвилевід. Порядок визначення складових поля спрямованих хвиль, страница 9

З урахуванням (1.10.12), вираз (1.10.9) перепишеться так:

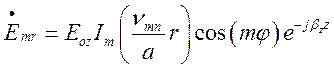                          (1.10.13)

Підставивши (1.10.13) у вирази (1.10.11) – (1.10.14) при  (поле електричного типу), отримаємо вирази для складових полів хвиль типів  у циліндричному (круглому) хвилеводі:

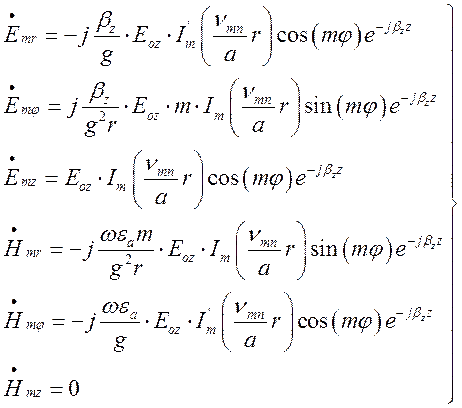 .               (1.10.14)

Повздовжнє хвильове число  визначається за формулою (1.3.7):

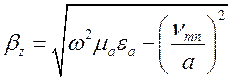 .                            (1.10.15)

Згідно (1.3.10) для хвиль типу  у циліндричному хвилеводі:

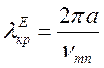,                                     (1.10.16)

їх фазова швидкість, виходячи з (1.5.2), дорівнюватиме:

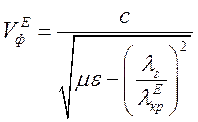 .                                (1.10.17)

а хвильовий опір, з урахуванням (1.6.9):

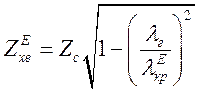
1.10.2 Хвилі магнітного типу

У таких хвилях тангенціальними до стінок хвилеводу будуть складові , які через 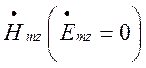 можна виразити за формулою(1.4.13):

.

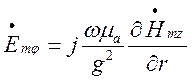Вираз для  знайдемо, розв’язавши рівняння Гельмгольця:

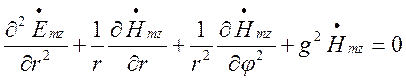.              (1.10.18)

Оскільки це рівняння за конструкцією збігається з рівнянням (1.10.1), то і розв’язок рівняння (1.10.18) за конструкцією збігається з виразом (1.10.13):

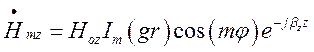 .                     (1.10.19)

Скориставшись тим, що складова  є тангенціальною до циліндричної стінки хвилеводу, то при  вона дорівнюватиме нулю і

,

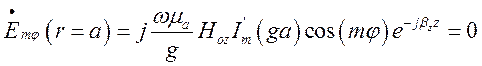звідки 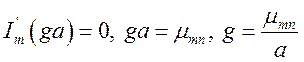                                                           (1.10.20)

де -n – й корінь першої похідної функції Бесселя  першого роду m –го порядку. Графіки  схожі на графіки , розглянуті вище. В табл. 1.10.2 наведені значення коренів декількох перших похідних функцій Бесселя .

Таблиця 1.10.2

n	m
	0	1	2
1	3,832	1,840	3,054
2	7,016	5,335	6,705
3	10,174	8,536	9,965
..	…	…	…

З урахуванням (1.10.20) вираз для  можна переписати так:

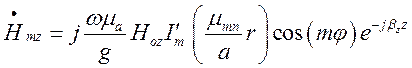.              (1.10.21)

Підставивши (1.10.21) в рівняння (1.4.11) – (1.4.14) при  матимемо вирази для складових хвиль типу  у круглому циліндричному хвилеводі:

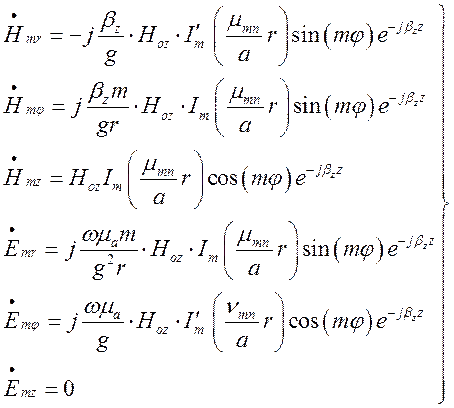 .                 (1.10.22)

Повздовжнє хвильове число  визначається за формулою (1.3.7):

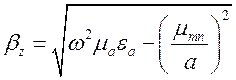.                             (1.10.23)

У відповідності до (1.3.10) для хвиль типу  у циліндричному хвилеводі:

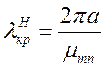.                                     (1.10.24)

Їх фазова швидкість, виходячи з (1.5.2), дорівнюватиме:

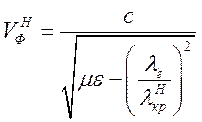                                       ,                                  (1.10.25)

а хвильовий опір, з урахуванням (1.6.15):

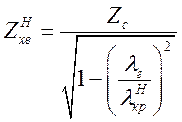 .                         (1.10.26)

1.11 Побудова картин поля хвиль  та  у циліндричному хвилеводі.

Побудову будемо здійснювати за наближеною методикою, наведеною у підрозділі 1.9. Нагадаємо попередньо, що перший індекс m вказує на кількість варіацій поля вздовж координатної лінії , яка у використаній системі координат є колом. Другий індекс n, очевидно, визначає кількість варіацій поля вздовж координати r (вздовж радіусу поперечного перетину хвилеводу). Зазначимо, що в прямокутному хвилеводі кількість варіацій поля завжди збігається з кількістю напівхвиль. У циліндричному хвилеводі варіація поля може збігатися як з напівхвильою, так і з чвертьхвильою. Все залежить від структури поля конкретної хвилі.

Розпочнемо побудову з хвиль  та , у яких відповідно немає варіацій (змін поля)  складової та  складової. Судячи по рівняннях (1.10.14) та (1.10.22) в циліндричному хвилеводі жодна з хвиль не можуть мати нульовим другий індекс, тобто хвилі  та  існувати не можуть.

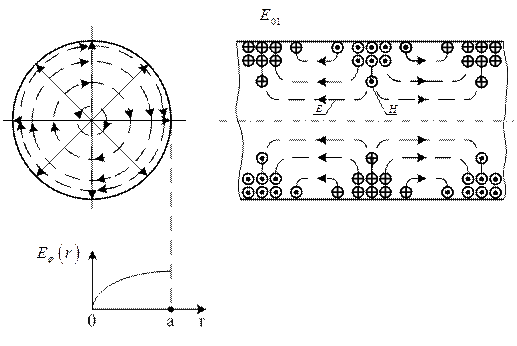
Рисунок 1.11.1

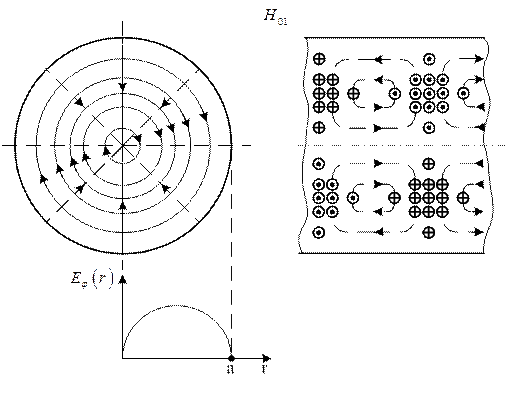
Рисунок 1.11.2

Хвиля  не має варіацій вздовж координати  (рис.1.11.1) тобто в поперечному перетині силові лінії магнітного поля є концентричними колами. Вздовж радіусу мається одна варіація , яка (рис.1.11.3) збігається з чвертьхвильою залежності . Хвиля  також не має варіації вздовж координати , силові лінії електричного поля теж утворюють концентричні кола. Але вздовж радіусу вкладається напівхвиля залежності , як видно на рис.1.11.2.

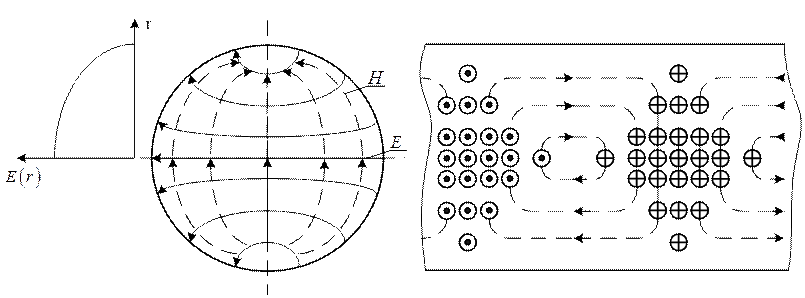
Рисунок 1.11.3