Введемо вектор 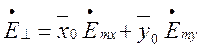 тоді з урахуванням виразів (1.6.1) - (1.6.4) маємо:
тоді з урахуванням виразів (1.6.1) - (1.6.4) маємо:
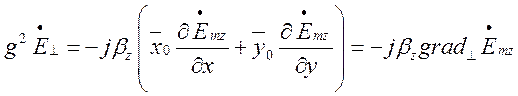 (1.6.5)
(1.6.5)
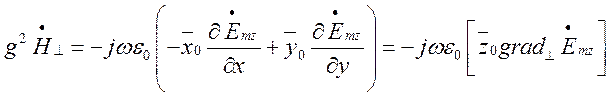 (1.6.6)
(1.6.6)
Визначивши 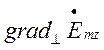 з виразу (1.6.5) і підставивши його у вираз (1.6.6),
отримаємо:
з виразу (1.6.5) і підставивши його у вираз (1.6.6),
отримаємо:
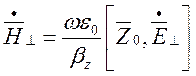 , (1.6.7)
, (1.6.7)
Тобто вектори ![]() і
і ![]() у хвиль типу Е є взаємно перпендикулярними.
Тоді вираз (1.6.7) можна переписати у скалярному вигляді:
у хвиль типу Е є взаємно перпендикулярними.
Тоді вираз (1.6.7) можна переписати у скалярному вигляді:
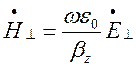
або
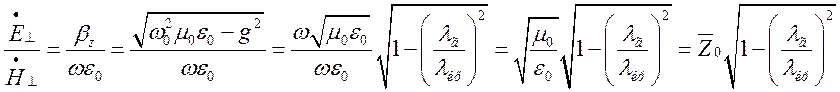 ,
,
де 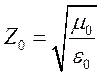 - хвильовий опір вакууму, який заповнює
хвилевід
- хвильовий опір вакууму, який заповнює
хвилевід ![]() .
.
Відношення поперечної складової електричного поля ![]() до поперечної складової магнітного поля
до поперечної складової магнітного поля ![]() називається хвильовим опором
хвилеводу
називається хвильовим опором
хвилеводу![]() . Отже, хвильовий опір хвилеводу з хвилею Е
типу
. Отже, хвильовий опір хвилеводу з хвилею Е
типу ![]() буде дорівнювати:
буде дорівнювати:
 (1.6.8)
(1.6.8)
У випадку, коли хвилевід заповнений діелектриком з параметрами ![]() то
то
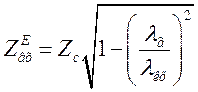 , (1.6.9)
, (1.6.9)
де 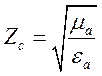 .
.
Для
електромагнітних хвиль Н типу ![]() з рівнянь (1.6.7) – (1.6.9) матимемо:
з рівнянь (1.6.7) – (1.6.9) матимемо:
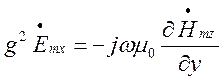 (1.6.10)
(1.6.10)
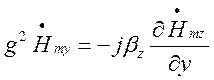 (1.6.11)
(1.6.11)
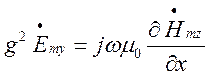 (1.6.12)
(1.6.12)
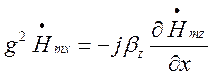 (1.6.13)
(1.6.13)
Діючи аналогічно попередньому випадку (випадку для хвиль Е типу), з урахуванням виразів (1.6.10) - (1.6.13) матимемо:
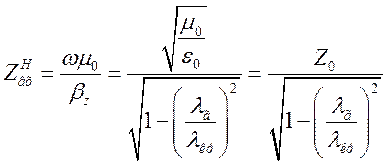 , (1.6.14)
, (1.6.14)
або 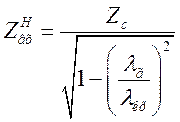 , (1.6.15)
, (1.6.15)
коли хвилевід заповнений діелектриком з хвильовим опором ![]() .
.
1.7 Прямокутний хвилевід
Прямокутний хвилевід, який є представником спрямовуючих систем, представляє собою металеву трубу прямокутного перетину. У такому хвилеводі можуть поширюватися хвилі

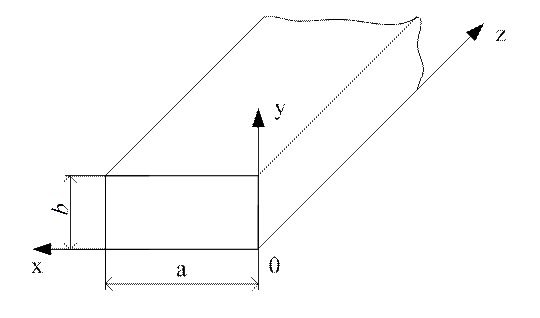
Рисунок 1.7.1
Е та Н типів. Розмістимо хвилевід у декартові системі координат, як це показано на рис 1.7.1.
1.7.1 Хвилі електричного типу
Складові поля Е хвиль будемо визначати за порядком, викладеним у підрозділі 1.4. Запишемо рівняння Гельмгольця для спрямованих хвиль (1.3.5), яке у даному випадку буде таким:
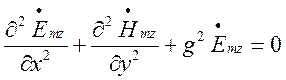 (1.7.1)
(1.7.1)
Розв’яжемо це рівняння, розділивши змінні за методом Фур’є. Для цього його розв’язок представимо у вигляді добутку:
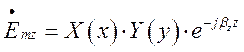 (1.7.2)
(1.7.2)
де ![]() - є функція лише координат
- є функція лише координат ![]() - функція лише координат
- функція лише координат![]() .
.
Підставивши (1.7.2) в (1.7.1) і розділивши отриманий
результат на ![]() матимемо:
матимемо:
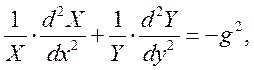 (1.7.3)
(1.7.3)
де х та у – незалежні змінні, що і дало право нам замінити частинні похідні на повні.
У лівій частині рівняння (1.7.3) маємо суму двох
функцій, які є незалежними одна від одної. Сума цих функцій дорівнює сталій
величині![]() . Це можливо, коли кожна з них буде
дорівнювати своїй сталій величині, тобто:
. Це можливо, коли кожна з них буде
дорівнювати своїй сталій величині, тобто:
 та
та 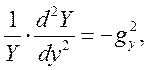 (1.7.4)
(1.7.4)
де ![]() .
.
Перепишемо рівняння (1.7.4) у такому вигляді:
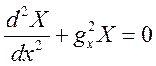 та
та 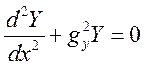 (1.7.5)
(1.7.5)
Як відомо з курсу вищої математики, такі лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами мають загальні розв’язки виду:
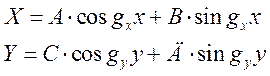 (1.7.6)
(1.7.6)
Після підстановки (1.7.6) в (1.7.2) для повздовжньої
складової ![]() хвилі матимемо:
хвилі матимемо:
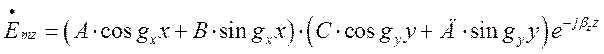 (1.7.7)
(1.7.7)
Виходячи з граничних умов для ![]() на стінках хвилеводу (ця складова є
тангенціальною до них) запишемо:
на стінках хвилеводу (ця складова є
тангенціальною до них) запишемо:
1)
При ![]() (права стінка хвилеводу):
(права стінка хвилеводу):
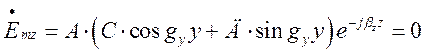 .
.
У цьому виразі один зі співмножників має дорівнювати
нулю при будь – яких значеннях y та
z. Це можливо лише коли ![]() а отже:
а отже:
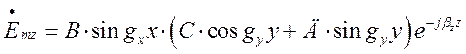 .
.
2)
При ![]() (ліва стінка хвилеводу):
(ліва стінка хвилеводу):
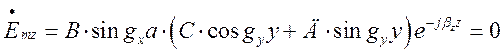 .
.
Що можливо при ![]() . Звідки
. Звідки ![]() і
і
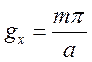 , (1.7.8)
, (1.7.8)
а отже 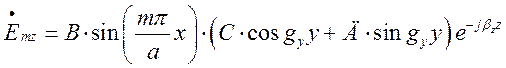 .
.
3)
При ![]() (нижня стінка хвилеводу):
(нижня стінка хвилеводу):
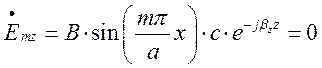 ,
,
звідки ![]() і
і 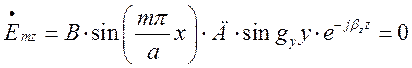 .
.
4)
При ![]() (верхня стінка хвилеводу):
(верхня стінка хвилеводу):
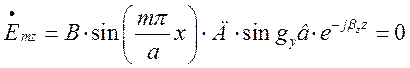 ,
,
звідки ![]() ,
, ![]() і
і
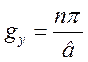 , (1.7.9)
, (1.7.9)
а отже 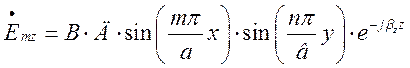 .
.
Оскільки розмірність добутку довільних коефіцієнтів інтегрування, як
бачимо з останнього виразу, збігається з розмірністю ![]() введемо позначення
введемо позначення ![]() і тоді:
і тоді:
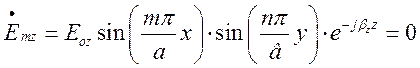 . (1.7.10)
. (1.7.10)
Поперечні складові знайдемо, скориставшись формулами (1.6.1) – (1.6.4):
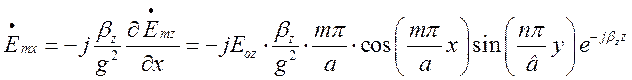 ,
,
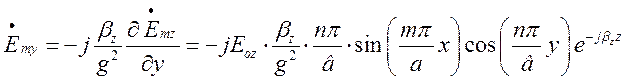 ,
,
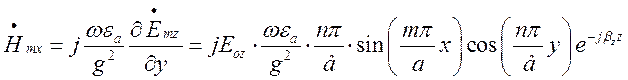 ,
,
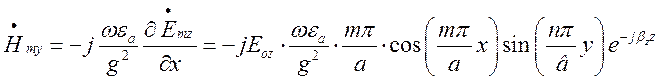 .
.
Таким чином, вираз для комплексних амплітуд складових поля Е хвилі у прямокутному хвилеводі мають вигляд:
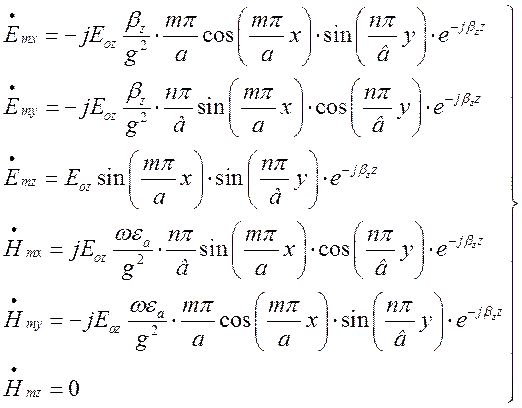 (1.7.11)
(1.7.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.