Як відомо з виразу (1.3.10)
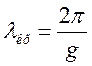 . Зваживши що ,
. Зваживши що , 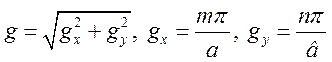 вираз для критичної довжини хвилі Е типу у
прямокутному хвилеводі матиме вигляд:
вираз для критичної довжини хвилі Е типу у
прямокутному хвилеводі матиме вигляд:
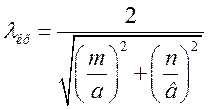 . (1.7.12)
. (1.7.12)
З виразів (1.7.11) випливає, що структура поля Е хвиль
у площині поперечного перетину прямокутного хвилеводу відповідає структурі
стійних хвиль. Число mдорівнює кількості напівхвиль, які розміщуються вздовж стінки а,
n – числу напівхвиль, що розміщуються вздовж стінки в.
Кожній парі чисел m і n
відповідає певна структура електромагнітного поля, яке позначається через ![]() . Якщо, наприклад
. Якщо, наприклад ![]() і
і ![]() то мова йде про поле типу
то мова йде про поле типу![]() .
.
1.7.2 Хвилі магнітного типу
Для такого типу хвиль необхідно повздовжну складову поля визначити, розв’язавши рівняння (1.3.6) після проектування його на вісь OZ:
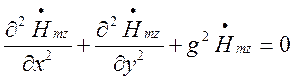 (1.7.13)
(1.7.13)
Діючи аналогічно до попереднього випадку (знаходження![]() ), знаходимо вираз для
), знаходимо вираз для![]() :
:
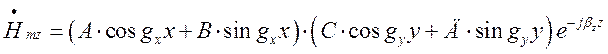 (1.7.14)
(1.7.14)
Для знаходження коефіцієнтів інтегрування ![]() скористуємось виразами (1.4.7) та (1.4.9) для
магнітних хвиль
скористуємось виразами (1.4.7) та (1.4.9) для
магнітних хвиль 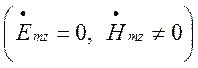 і запишемо пропорції:
і запишемо пропорції:
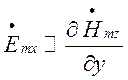 та
та 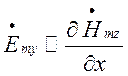 .
.
1)
При ![]() (нижня стінка хвилеводу):
(нижня стінка хвилеводу):
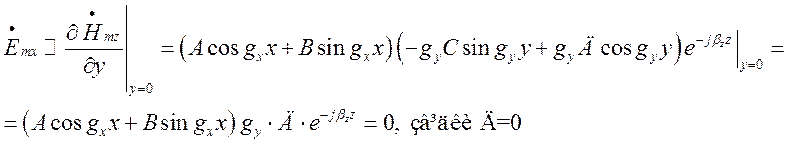
2)
При ![]() (верхня
частина хвилеводу):
(верхня
частина хвилеводу):

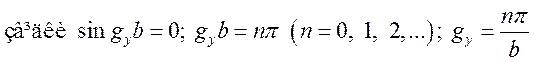 .
.
3)
При ![]() (права стінка хвилеводу):
(права стінка хвилеводу):
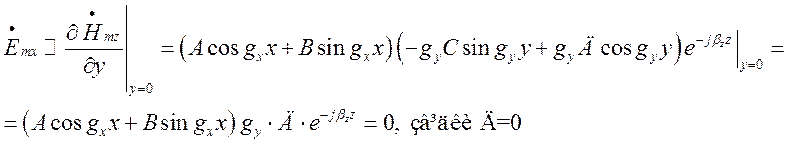
4)
При ![]() (ліва стінка хвилеводу):
(ліва стінка хвилеводу):
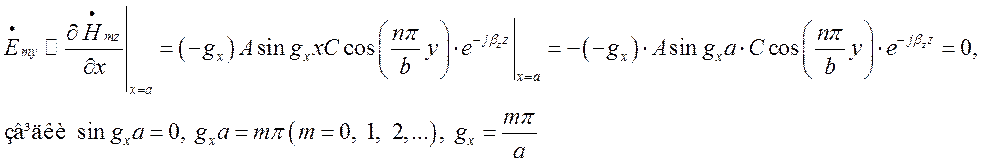
Як бачимо, вирази для поперечних чисел ![]() та
та ![]() збігаються
з попереднім випадком, а отже, критична довжина хвилі у випадку магнітних хвиль
має визначитися також за формулою (1.7.12). Зміст індексів m і nтеж є тим самим що і у випадку хвиль Еmn,
наприклад, у випадку хвилі
збігаються
з попереднім випадком, а отже, критична довжина хвилі у випадку магнітних хвиль
має визначитися також за формулою (1.7.12). Зміст індексів m і nтеж є тим самим що і у випадку хвиль Еmn,
наприклад, у випадку хвилі ![]() , вздовж розмірів a і в розміщується по одній півхвилі.
, вздовж розмірів a і в розміщується по одній півхвилі.
Вираз для повздовжньої складової ![]() буде
таким:
буде
таким:
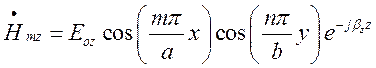 .
.
Аналогічно до попереднього випадку електричної хвилі, поперечні
складові знайдемо, підставивши у вирази (1.4.7) - (1.4.10) ![]() та
та ![]() з
(1.7.15):
з
(1.7.15):
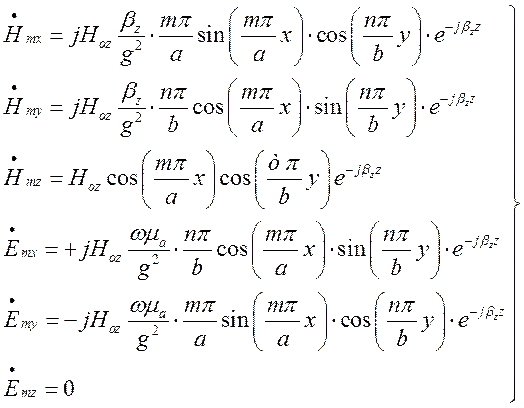 (1.7.16)
(1.7.16)
1.7.3 Умови існування хвиль різних типів у прямокутному хвилеводі
Щоб хвиля заданого типу могла поширюватись у заданому хвилеводі, необхідно виконати умову (1.3.11), яку, з урахуванням (1.7.12), можна переписати так:
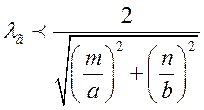 (1.7.17)
(1.7.17)
Судячи з виразу (1.7.11) для хвиль електричного типу,
індекси mабоn не
можуть дорівнювати нулю. Тобто у прямокутному хвилеводі не можливе існування
хвиль типу ![]() або
або ![]() .
.
Для хвилі 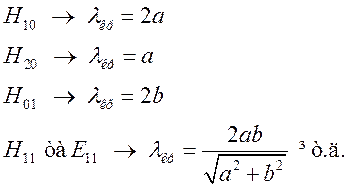
На практиці найпоширенішими є прямокутні хвилеводи, у
яких ![]() . Наприклад,
. Наприклад, ![]() ,
або
,
або ![]() .
.
Найбільшу критичну довжину хвилі має хвиля ![]() , далі
, далі ![]()
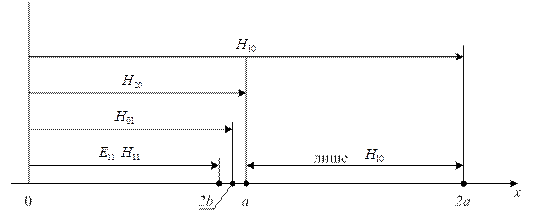
Рисунок 1.7.2
На рис.1.7.2 показані межі довжин хвиль генератора,
при яких можуть існувати декілька типів хвиль або мод (від англ. mode – тип хвилі). Та мода, яка має найбільшу критичну довжину хвилі
називається основною модою (основним типом хвиль, основною хвильою). Серед
хвиль електричного типу основною є хвиля ![]() ,
серед магнітних хвиль -
,
серед магнітних хвиль - ![]() , остання є
основною і в прямокутному хвилеводі.
, остання є
основною і в прямокутному хвилеводі.
Якщо у хвилеводі існують одночасно дві і більше мод,
то такий хвилевід, кажуть, працює у багатомодовому режимі (є багатомодовим
хвилеводом). Покажемо, за яких умов прямокутний хвилевід буде в одномодовому
режимі, тобто у ньому зможе поширюватися лише основна хвиля ![]() .
.
Умовою її існування є ![]() ,
умовою відсутності найближчої до неї моди
,
умовою відсутності найближчої до неї моди ![]() ,
тобто:
,
тобто:
![]() . (1.7.18)
. (1.7.18)
Відсутність моди ![]() гарантується
умовою:
гарантується
умовою: ![]() . Можна сформулювати і зворотню
задачу: якими мають бути поперечні розміри прямокутного хвилеводу, щоб при
заданому діапазоні довжин хвиль генератора у хвилеводі забезпечувався
одномодовий режим роботи.
. Можна сформулювати і зворотню
задачу: якими мають бути поперечні розміри прямокутного хвилеводу, щоб при
заданому діапазоні довжин хвиль генератора у хвилеводі забезпечувався
одномодовий режим роботи.
Припустимо ![]() Тоді умова
існування хвилі
Тоді умова
існування хвилі ![]() буде такою:
буде такою:
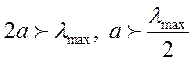 .
.
Відсутність хвилі ![]() вимагає, щоб
вимагає, щоб ![]() , а відсутність
, а відсутність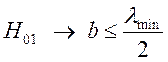 . Отже:
. Отже:
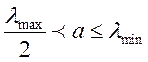 ;
; 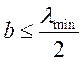 .
.
1.8 Аналітичний метод побудови картини поля хвилі ![]() у прямокутному хвилеводі.
у прямокутному хвилеводі.
Для визначення виразів складових поля хвилі ![]() в (1.7.16) покладемо
в (1.7.16) покладемо ![]() і отримаємо:
і отримаємо:
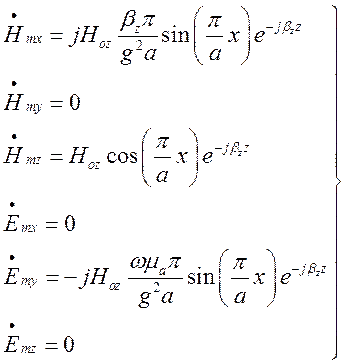 (1.8.1)
(1.8.1)
Отже, хвиля ![]() у прямокутному
хвилеводі має лише три складових поля:
у прямокутному
хвилеводі має лише три складових поля: ![]() .
Знайдемо вирази для миттєвих значень цих векторів поля.
.
Знайдемо вирази для миттєвих значень цих векторів поля.
Комплекси відповідних векторів поля знайдемо,
домноживши комплексні амплітуди (1.8.1) на ![]() :
:
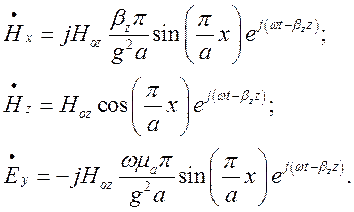
Застосувавши до останніх виразів символічної операції виділення дійсної частини, отримаємо:
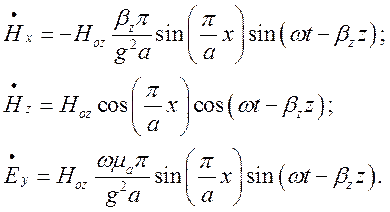
Для моменту часу ![]() ,
отримані вирази перепишуться так:
,
отримані вирази перепишуться так:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.