Электротехника \ Электродинамика и распространение радиоволн

Хвилеводи. Спрямовуючі системи та спрямовані хвилі. Двоплощинний хвилевід. Порядок визначення складових поля спрямованих хвиль, страница 2

Якщо ж у досліджувальному процесі визначити ці векторні суми за умови , то картина поля над ідеально – провідною площиною буде такою, якою вона зображена на рис. 1.2.2.

У своєму русі плоска електромагнітна хвиля зміщується у правий бік (вздовж осі OZ). Цю вісь будемо називати повздовжньою, тоді, очевидно, осі OX та OY слід називати поперечними. Відповідно і складові (проекції) векторів поля результуючої хвилі будемо називати:  - поперечними, а  і - повздовжніми.

В побудованій картині поля є такі складові а . Отже, ця хвиля має повздовжню складову вектора  і не має повздовжньої складової  поля  а тому цю хвилю слід віднести до хвиль  типу (електричних хвиль).

У напрямку осі OX спостерігається певна періодичність. Щоб у ній розібратися, давайте спробуємо «заставити» електромагнітну хвилю рухатися вздовж осі OZ. Для цього на певній відстані від ідеально – провідної площини розмістимо другу таку ж саму площину зверху. Таким чином, хвиля, відбиваючись від «підлоги» та «стелі», буде поширюватись у потрібному нам напрямку (вздовж осі OZ).

  Відстань між цими площинами має бути такою, щоб не порушилися граничні умови для векторів поля, що збереже структуру поля непорушною. Найменшою відстанню є відстань a ( рис.1.2.3а), далі відстань 2а ( рис.1.2.3б) і т.д. На відстані а вектори поля змінюють свій напрямок на протилежний один раз ( одна напівхвиля), а тому така хвиля називається хвилею типу E1. На рис. 1.2.3б, очевидно, зображено картину поля хвилі типу E2. Через невизначеність поперечного розміру у випадку рис. 1.2.2, кажуть, що йдеться про поля хвилі Em- типу, де m може приймати значення 1,2,3,… .

  Спрямовуючі системи, зображені на рис.1.2.3, називаються двоплощинними хвилеводами.

Випадок другий. Вектор E перпендикулярний до площини падіння (рис.1.2.4)

Міркуючи аналогічно першому випадку, легко побудувати картини поля хвилі H типу ( магнітної хвилі). Відмінність буде полягати у визначенні напрямів векторів поля Eb та Hb у слідах  фронтів відбитої хвилі.

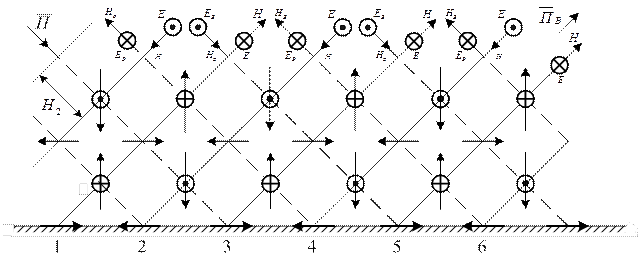
Рисунок 1.2.4

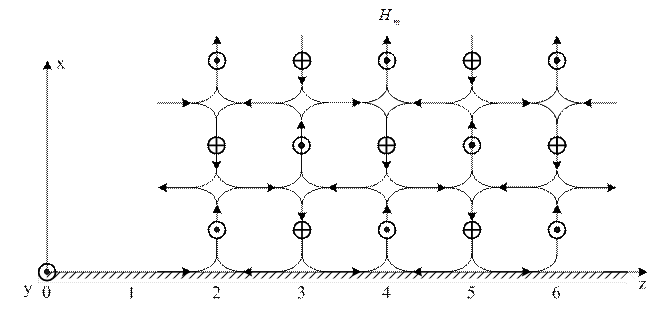
Рисунок 1.2.5

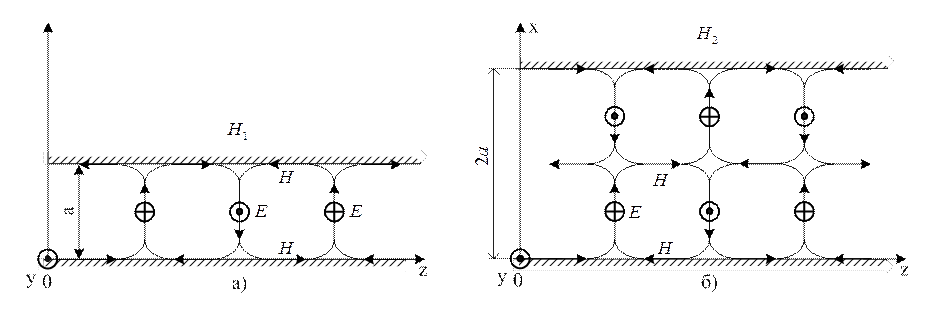Рисунок 1.2.6

Справа у тім, що хвиля Н має лише одну складову , яка при падінні є тангенціальною до ідеально – провідної площини. Відомо з граничних умов, що ця складова дорівнює нулю, тобто . Звідки . На рис.1.2.5 показана структура поля електромагнітної хвилі типу , на рис.1.2.6 – хвилі типу  і .

Як бачимо, магнітні складові лінії полів у обох випадках є замкнутими, тобто магнітне поле може бути лише вихровим. Електричне поле (випадок 1-й) проявляє дуалізм, коли воно має і вихровий і потенціальний характер в одній і тій самій хвилі (рис.1.2.3б). в структурі ж хвилі  електричні складові лінії не є замкнутими, тобто електричне поле тут носить чисто потенціальний характер.

1.3 Однорідні рівняння Гельмгольця для спрямованих хвиль.

Критична частота.

Розглянемо довільну спрямовану систему, яка буде відповідати таким вимогам:

—  нескінченна довжина, що гарантує поширення в ній лише прямої хвилі (відбиття від кінця системи нема);

—  прямолінійна (хвилевод немає згинів);

—  стінки є ідеально-провідними (нема втрат в провідниках);

—  заповненням є вакуум (нема втрат в діелектрику);

—  форма та розміри поперечного перетину є однаковими на усій довжині системи.

Така ідеалізація спрямовуючої системи (хвилеводу) допоможе нам краще розібратися в задачах, поставлених у цьому підрозділі посібника.

Запишемо однорідні рівняння Гельмгольця для необмеженого вільного простору:

,

.

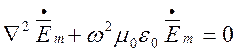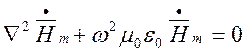Оскільки       ці рівняння, при відсутності сторонніх джерел, задовільняють вектори напруженості монохроматичних електричного і магнітного полів, будемо шукати частинні розв’язки цих рівнянь для випадку монохроматичних полів, які поширюються вздовж ідеальної спрямовуючої системи. При цьому, очевидно, залежність векторів  та  від повздовжньої координати Z має описуватись множником , де - повздовжнє хвильове число, яке вказує на швидкість зростання фази хвилі у напряму осі OZ. Отже, розв’язки цих рівнянь можна представити виразами:

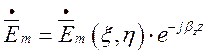                                    ,                                             (1.3.1)

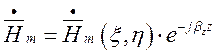                                    ,                                   (1.3.2)

Скачать файл