Оскільки у хвилях Е типу складова![]() , а у хвилях Н типу складова
, а у хвилях Н типу складова![]() , то фактично праві частини виразів
для поперечних складових через повздовжні (1.4.7) - (1.4.14) будуть удвічі
коротшими для хвиль конкретних типів.
, то фактично праві частини виразів
для поперечних складових через повздовжні (1.4.7) - (1.4.14) будуть удвічі
коротшими для хвиль конкретних типів.
1.5 Дисперсія в хвилеводах
Фазова швидкість, під якою будемо розуміти швидкість
руху фазового фронту спрямованої хвилі вздовж осі OZ, визначається за формулою:
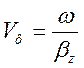 враховуючи (1.3.7) цю формулу
перепишемо так:
враховуючи (1.3.7) цю формулу
перепишемо так: 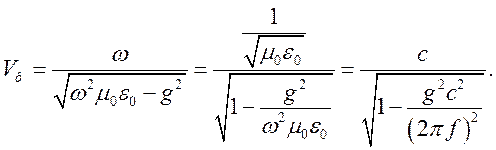
Враховуючи (1.3.10) отримаємо:
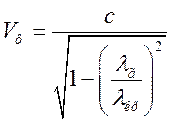 (1.5.1)
(1.5.1)
Якщо хвилевід заповнений діелектриком з параметрами ![]() то останній вираз слід переписати
так:
то останній вираз слід переписати
так:
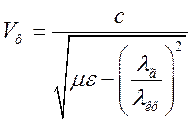 . (1.5.2)
. (1.5.2)
Хвиля, що поширюється вздовж хвилеводу представляє
собою гармонічне коливання, періодичність якого буде визначатися довжиною хвилі
у хвилеводі (фазовою довжиною хвилі): ![]() де
Т – період монохроматичної хвилі
де
Т – період монохроматичної хвилі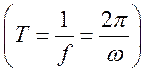 .
Добуток
.
Добуток ![]() - довжині хвилі генератора. З
урахуванням сказаного вираз (1.5.2) матиме вигляд:
- довжині хвилі генератора. З
урахуванням сказаного вираз (1.5.2) матиме вигляд:
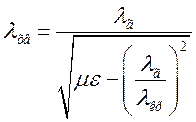 . (1.5.3)
. (1.5.3)
Зваживши на те, що групова швидкість 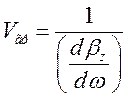 , нескладно отримати формулу для
визначення групової швидкості спрямованої хвилі:
, нескладно отримати формулу для
визначення групової швидкості спрямованої хвилі:
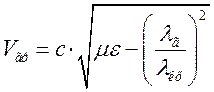 . (1.5.4)
. (1.5.4)
Залежності фазової та групової швидкості від довжини хвилі генератора називається дисперсними характеристиками спрямованої хвилі, а саме явище – дисперсією. Зауважимо, що у спрямовуючій системі на відміну від необмеженого простору дисперсія має місце і при відсутності втрат, про що свідчить вираз (1.5.1).
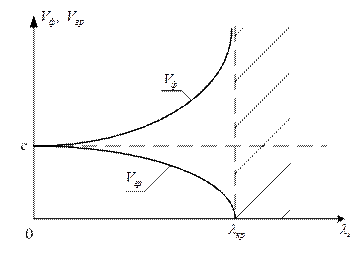
Рисунок 1.5.1
Як випливає з виразу (1.5.1) та рис. 1.5.1 фазова
швидкість спрямованої хвилі завжди перевищує швидкість світла і при ![]() вона стає нескінченно великою.
Групова ж швидкість при наближенні
вона стає нескінченно великою.
Групова ж швидкість при наближенні ![]() до
до ![]() зменшується до нуля.
зменшується до нуля.
Пояснимо це, скориставшись концепцією парціальних хвиль. У двоплощинному хвилеводі, наприклад, парціальна плоска хвиля поширюється вздовж хвилеводу відбиваючись від нижньої та верхньої ідеально – провідних площин. Нехай парціальна плоска

Рисунок 1.5.2
Хвиля, збуджена у точці О(рис.1.5.2),
зі швидкістю с прямує до верхньої площини хвилеводу і падає на
неї у точці Апід кутом φ За одну секунду фронт Ф цієї
хвилі, залишаючись перпендикулярним до вектора її швидкості с,
переміститься на відстань ОК. Отже, довжина відрізка ОК дорівнює
довжині вектора фазової швидкості хвилі (швидкості переміщення фронту хвилі
вздовж хвилеводу, яку будемо називати швидкістю хвилі у хвилеводі) ![]() . Енергія хвилі за цей час вздовж
хвилеводу пройде відстань
. Енергія хвилі за цей час вздовж
хвилеводу пройде відстань ![]() (групова швидкість),
яка дорівнюватиме довжині проекції вектора с на вісь OZ.
(групова швидкість),
яка дорівнюватиме довжині проекції вектора с на вісь OZ.
Розглянувши прямокутні трикутники, можемо записати:
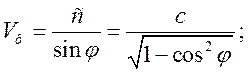
![]() (1.5.5)
(1.5.5)
Порівнявши вирази (1.5.1) і для ![]() (1.5.5) та (1.5.4) при
(1.5.5) та (1.5.4) при ![]() і для
і для ![]() (1.5.5):
(1.5.5):
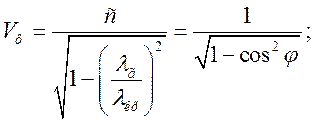
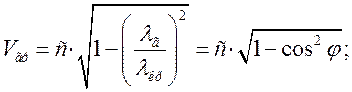
маємо право записати: 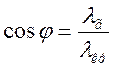 .
.
Якщо довжина хвилі генератора ![]() буде більшою за
буде більшою за![]() , то відношення
, то відношення ![]() стане більшим, значить кут падіння
стане більшим, значить кут падіння ![]() має бути меншим від
має бути меншим від ![]() (хвиля падатиме крутіше). На рис.1.5.2 хвиля
падає у точку Б. фазовий фронт Ф за одну секунду пройду шлях
(хвиля падатиме крутіше). На рис.1.5.2 хвиля
падає у точку Б. фазовий фронт Ф за одну секунду пройду шлях![]() , і фазова швидкість хвилі зросте до значення V’Ф >VФ.
Групова ж швидкість зменшиться до значення V’гр
< Vгр.
, і фазова швидкість хвилі зросте до значення V’Ф >VФ.
Групова ж швидкість зменшиться до значення V’гр
< Vгр.
Коли ж довжина хвилі генератора досягне значення![]() , кут падіння на верхню площину хвилеводу
дорівнюватиме нулю, тобто хвиля падатиме перпендикулярно до стінки у точку В.
Фазовий фронт цієї хвилі буде паралельним осі OZі їх перетин
відбудеться на нескінченно великій відстані від точки О
, кут падіння на верхню площину хвилеводу
дорівнюватиме нулю, тобто хвиля падатиме перпендикулярно до стінки у точку В.
Фазовий фронт цієї хвилі буде паралельним осі OZі їх перетин
відбудеться на нескінченно великій відстані від точки О![]() .
.
Групова швидкість дорівнюватиме нулю![]() . Тобто хвиля буде відбиватися від стінок
хвилеводу, рухаючись лише у поперечному напрямку без переміщення вздовж
хвилеводу. Таким чином критичну довжину хвилі у хвилеводі можна визначити як
таку, при якій припиняється поширення хвилі у хвилеводі. Умовою ж
можливості поширення цієї хвилі є нерівність:
. Тобто хвиля буде відбиватися від стінок
хвилеводу, рухаючись лише у поперечному напрямку без переміщення вздовж
хвилеводу. Таким чином критичну довжину хвилі у хвилеводі можна визначити як
таку, при якій припиняється поширення хвилі у хвилеводі. Умовою ж
можливості поширення цієї хвилі є нерівність:
![]() або
або![]() (1.5.6)
(1.5.6)
1.6 Хвильовий опір хвилеводу
Для електромагнітних хвиль Е типу ![]() у спрямовуючий системі, наприклад, у
двоплощинному хвилеводі, вирази (1.4.7)-(1.4.10) перепишуться так:
у спрямовуючий системі, наприклад, у
двоплощинному хвилеводі, вирази (1.4.7)-(1.4.10) перепишуться так:
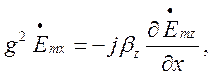 (1.6.1)
(1.6.1)
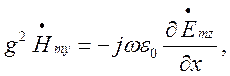 (1.6.2)
(1.6.2)
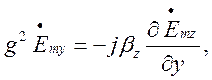 (1.6.3)
(1.6.3)
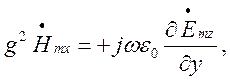 (1.6.4)
(1.6.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.