хвиля ![]() має по одній варіації вздовж
координати
має по одній варіації вздовж
координати ![]() та
та ![]() .
Як бачимо, вздовж радіусу вектора Е має максимум при
.
Як бачимо, вздовж радіусу вектора Е має максимум при ![]() і дорівнює нулю при
і дорівнює нулю при ![]() , варіація збігається з
чвертьхвильою. Вздовж координатної лінії
, варіація збігається з
чвертьхвильою. Вздовж координатної лінії ![]() цей
самий вектор (при зміненні
цей
самий вектор (при зміненні ![]() від
від ![]() ) має максимум при
) має максимум при ![]() і мінімум на обох кінцях цього
інтервалу, варіація збігається з напівхвильою.
і мінімум на обох кінцях цього
інтервалу, варіація збігається з напівхвильою.
Судячи по формулах (1.10.16),
(1.10.24) та таблицях 1.10.1, 1.10.2, найдовшу критичну довжину хвилі має хвиля
типу ![]() :
:
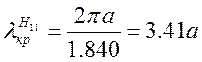 ,
,
вона і є основною модою у круглому циліндричному хвилеводі.
Серед хвиль електричного типу
найбільшу довжину хвилі, має хвиля ![]() :
:
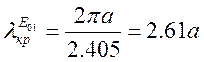 .
.
1.12 Коаксіальний хвилевід
Круглий коаксіальний хвилевід (або просто коаксіальний хвилевід) будемо розглядати у циліндричній системі координат (рис.1.12.1)
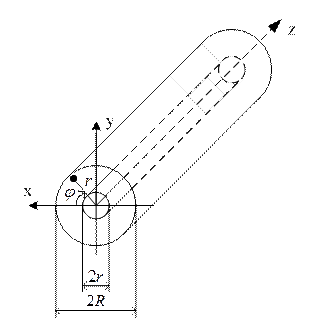
Рисунок 1.12.1
Такий хвилевід є двопровідною
лінією передачі електромагнітної енергії. Два циліндричних провідники,
зовнішній радіусом R і внутрішній - r
мають спільну вісь ![]() (Ко – спільна, аксіс
- вісь).
(Ко – спільна, аксіс
- вісь).
Ці два провідники розділені
діелектриком без втрат з параметрами ![]() . У такому
хвилеводі можуть поширюватись як хвилі типу Т (поперечні), так і хвилі Е
та Н типів.
. У такому
хвилеводі можуть поширюватись як хвилі типу Т (поперечні), так і хвилі Е
та Н типів.
Поширення Е та Н хвиль відбувається шляхом багатократного відбиття поля від внутрішньої поверхні зовнішнього провідника (труби) й зовнішньої поверхні внутрішнього провідника (стрижня), аналогічно тому як це відбувається у прямокутному чи круглому циліндричному хвилеводах.
Оскільки коаксіальний хвилевід має цілий ряд корисних особливостей саме при поширенні у ньому хвилі Т типу, у подальшому зупинимося саме на цьому випадку.
1.12.1 Хвилі Т типу.
Через те, що у хвилях типу Т
відсутні повздовжні складові поля ![]() , вирази (1.4.11)
– (1.4.14) перепишуться таким чином:
, вирази (1.4.11)
– (1.4.14) перепишуться таким чином:
![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Оскільки усі ці чотири
складові не можуть дорівнювати нулю, витікає, що поперечне хвильове число ![]() , а критична довжина хвилі такого
поля
, а критична довжина хвилі такого
поля
![]() .
.
Це означає, що по коаксіальному хвилеводу може поширюватися хвиля будь – якої низької частоти, включаючи постійний струм. В усіх цих випадках структура поля буде однією і тією ж самою у поперечному перетині.
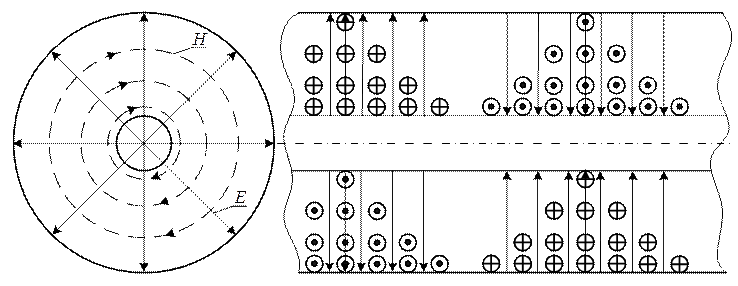
Рисунок 1.12.1
Отже, хвилі Т типу у
круглому коаксіальному хвилеводі мають дві складових поля: ![]() та
та ![]() .
.
Оскільки ![]() , то дисперсія у такому хвилеводі
буде відсутня, згідно з формулою (1.5.2)
, то дисперсія у такому хвилеводі
буде відсутня, згідно з формулою (1.5.2)
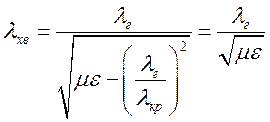 ,
,
де ![]() - довжина хвилі генератора, виміряна
у вільному просторі (вакуумі). Сухе повітря Земної атмосфери має
- довжина хвилі генератора, виміряна
у вільному просторі (вакуумі). Сухе повітря Земної атмосфери має ![]() і
і ![]() ,
а тому у коаксіальному хвилеводі, заповненому таким повітрям,
,
а тому у коаксіальному хвилеводі, заповненому таким повітрям, ![]() .
.
Повернувшись до (1.4.11) – (1.4.14), бачимо, що для хвилі Т типу цими виразами скористатися не можливо. А тому для визначення складових поля Т хвилі у коаксіальному хвилеводі звернемося до 1-го рівняння Максвелла, записаного для комплексних амплітуд в інтегральній формі:
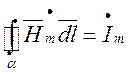 (1.12.2)
(1.12.2)
Під струмом ![]() у даному випадку слід розуміти
електричний струм, який протікає по центральному провіднику хвилеводу.
Електромагнітна Т хвиля поширюється вздовж осі
у даному випадку слід розуміти
електричний струм, який протікає по центральному провіднику хвилеводу.
Електромагнітна Т хвиля поширюється вздовж осі ![]() хвилеводу
зі швидкістю світла у середовищі, що заповнює хвилевід. З такою самою швидкістю
має поширюватись і електричний струм вздовж хвилеводу. Вважаючи втрати у
хвилеводі відсутніми, стала поширення к дорівнює коефіцієнту фази
хвилеводу
зі швидкістю світла у середовищі, що заповнює хвилевід. З такою самою швидкістю
має поширюватись і електричний струм вздовж хвилеводу. Вважаючи втрати у
хвилеводі відсутніми, стала поширення к дорівнює коефіцієнту фази ![]() . Змінення фази вздовж осі
. Змінення фази вздовж осі ![]() підпорядковане закону
підпорядковане закону ![]() . Отже, струм, який протікає вздовж
хвилеводу:
. Отже, струм, який протікає вздовж
хвилеводу:
![]() (1.12.3)
(1.12.3)
Цей струм збуджує вихрове
магнітне поле навколо центрального провідника з напруженістю ![]() . Підставивши (1.12.3) у вираз
(1.12.2) отримаємо:
. Підставивши (1.12.3) у вираз
(1.12.2) отримаємо:
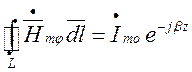 . (1.12.4)
. (1.12.4)
Або, оскільки ![]() і
і ![]() є
векторами спрямованими в один бік,
є
векторами спрямованими в один бік, 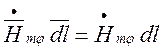 . Довжина
елементарної дуги
. Довжина
елементарної дуги ![]() контура Lдорівнює:
контура Lдорівнює:
![]() .
.
З урахуванням цих міркувань вираз (1.12.4) можна переписати таким чином:
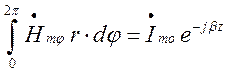 .
.
Як бачимо з рис.1.12.1,
магнітне поле не має варіацій (не змінюється) вздовж координати ![]() , то
, то ![]() можна
винести за знак інтегрування, і тоді:
можна
винести за знак інтегрування, і тоді:
![]()
звідки
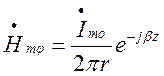 . (1.12.5)
. (1.12.5)
Вираз (1.12.5) визначає магнітну складову електромагнітного поля у коаксіальному хвилеводі хвилі Т типу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.