Хвилеводи. Спрямовуючі системи та спрямовані хвилі. Двоплощинний хвилевід. Порядок визначення складових поля спрямованих хвиль, страница 3

де ,  - поперечні координати відповідної ортогональної системи координат.

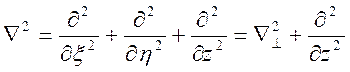
Нагадаємо, що оператор Лапласа (набла квадрат):

Підставивши (1.3.1) та (1.3.2) у рівняння Гельмгольця, отримаємо рівняння:

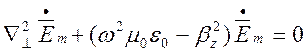                                    ,                              (1.3.3)                                                 

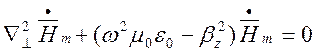                                     ,                            (1.3.4)

або, позначивши , матимемо рівняння:

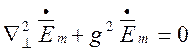                                         ,                                         (1.3.5)

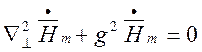                                                                                  (1.3.6)

які , як і (1.3.3) - (1.3.6) називаються рівняннями Гельмгольця для спрямованих хвиль, а g – поперечним хвильовим числом.

Повздовжне хвильове число  буде дорівнювати:

                                                                                   (1.3.7)

У виразах (1.3.1) та  (1.3.2) множник  вказує не на те, що хвиля поширюється вздовж хвилеводу. При цьому  - повинне бути дійсним числом.

Розглянемо такі можливі випадки:

1. , - дійсне число і хвиля буде поширюватися вздовж осі OZ хвилеводу.

2. , =0, поширення хвилі неможливе.

3. ,  - уявне число. Припустимо =-jp, де р – дійсне число. Тоді множник = з фазового перетворюється на амплітудний, тобто хвиля щвидко згасає вздовж осі OZ і поширюватися не може.

Отже, другий випадок є критичним, тобто умовою припинення поширення хвилі вздовж хвилеводу. Оскільки  є константами, другий випадок можливий на якійсь певній частоті роботи генератора. Назвемо цю частоту критичною і тоді:

                          або 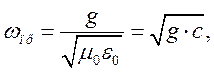                                     (1.3.8)

де 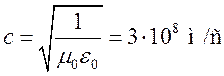- швидкість світла у вакуумі.

Таким чином, умовою поширення хвилі вздовж спрямовульної системи (хвилеводу) є вираз:

                                                                                                              (1.3.9)

де - кругова (циклічна) частота генератора хвилі. При  поширення хвилі у хвилеводі припиняється і при подальшому зменшенні частоти генератора поширення залишається неможливим. Режим роботи хвилеводу при  називається закритичним.

Критичній частоті відповідає критична довжина хвилі  яку визначаємо зваживши, що

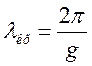                         :  або 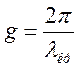                                (1.3.10)            

а умовою поширення хвилі є:

                                                                                                 (1.3.11)

1.4 Порядок визначення складових поля спрямованих хвиль

Для визначення виразів для складових поля спрямованих хвиль потрібно розв’язати векторні рівняння (1.3.5) та (1.3.6), а оскільки кожному з них відповідають три скалярних рівняння, то необхідно розв’язати шість рівнянь. Такий шлях є дуже громіздким. Виберемо інший шлях: розв’яжемо два скалярних рівняння Гельмгольця відносно повздовжніх складових  та, а чотири поперечних складових, скориставшись виразами для них, визначимо через знайдені повздовжні складові.

Для отримання таких виразів скористаємося проекціями 1-го та 2-го векторних рівнянь Максвелла, записаних у диференціальній формі для монохроматичних коливань:

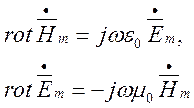
Декартова система координат

Проекції на вісь OX:

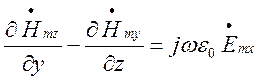                                     (1.4.1)

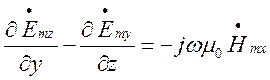                                   (1.4.2)

Проекції на вісь OY:

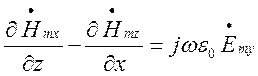                                               (1.4.3)

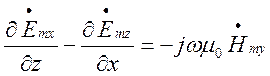                                   (1.4.4)

Оскільки у спрямовуючій системі 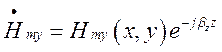, , 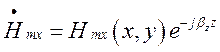, , 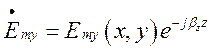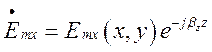складові з похідними по Z можна переписати так:

  

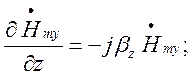
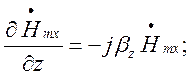
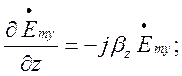
тоді вирази (1.4.1) – (1.4.4) матимуть вигляд:

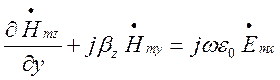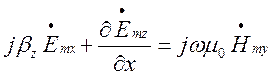,;                      (1.4.5)

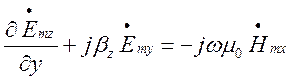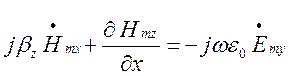,                    (1.4.6)

Розв’язуючи систему рівнянь (1.4.5) відносно  та систему (1.4.6) відносно, отримаємо:

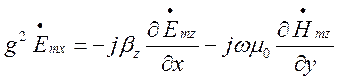,                        (1.4.7)

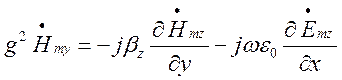,                      (1.4.8)

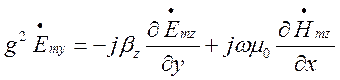,                        (1.4.9)

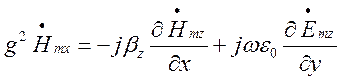.                        (1.4.10)

Циліндрична система координат

Діючи аналогічно, будемо мати:

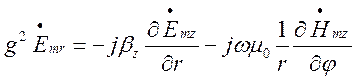,                      (1.4.11)

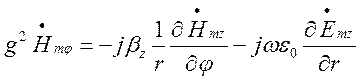,                    (1.4.12)

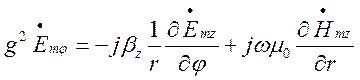,                     (1.4.13)

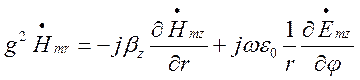.                     (1.4.14)