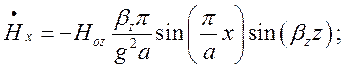 (1.8.2)
(1.8.2)
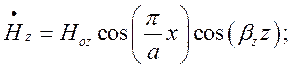 (1.8.3)
(1.8.3)
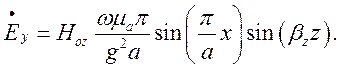 (1.8.4)
(1.8.4)
Як бачимо з (1.8.2) - (1.8.4), складові поля є гармонічними функціями координат x та z і від координати y не залежать. Множники, які передують гармонічним функціям мають розмірності відповідних складових поля і відображають їх амплітудні значення. Ввівши позначення:
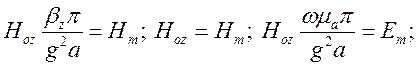
вирази для миттєвих значень складових поля хвилі ![]() перепишемо у такому вигляді:
перепишемо у такому вигляді:
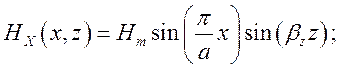 (1.8.5)
(1.8.5)
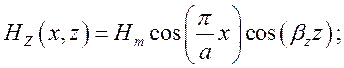 (1.8.6)
(1.8.6)
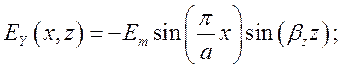 (1.8.7)
(1.8.7)
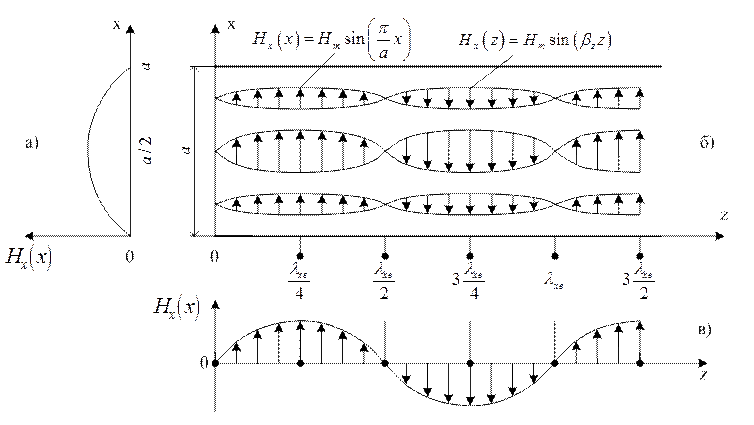
Рисунок 1.8.1
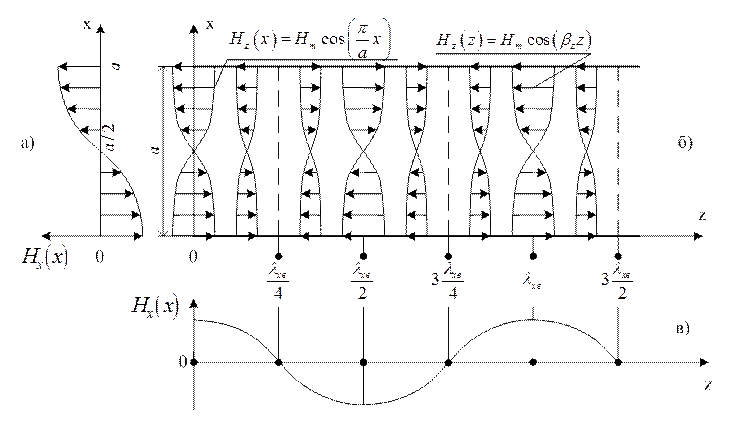
Рисунок 1.8.2
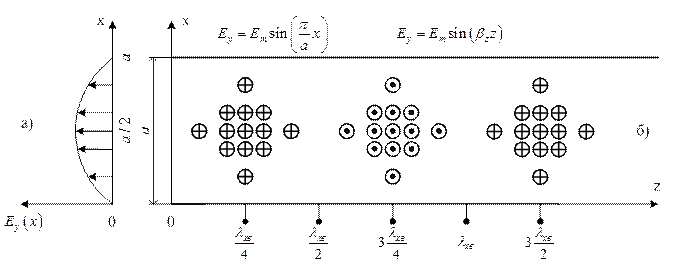
Рисунок 1.8.3
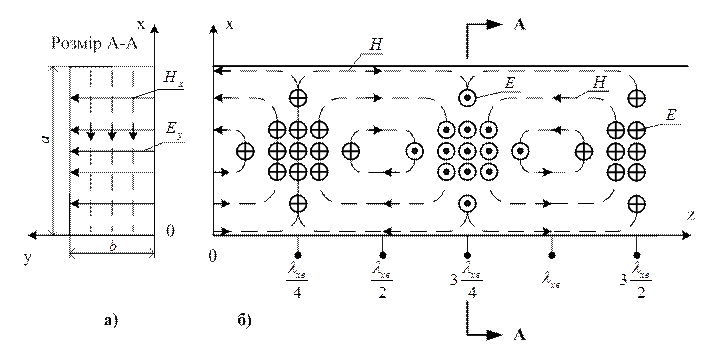
Рисунок 1.8.4
На рис.1.8.1а зображено еп’юру залежності складової ![]() від координати х. На
рис.1.8.1б – розташування
від координати х. На
рис.1.8.1б – розташування ![]() та характер її
залежності від координати х та z.
На рис.1.8.1в – еп’юру залежності складової
та характер її
залежності від координати х та z.
На рис.1.8.1в – еп’юру залежності складової ![]() від
координати z.
від
координати z.
На рис.1.8.2 зображені еп’юри залежності ![]() від координати х(а),
координати z(в) та
розташування
від координати х(а),
координати z(в) та
розташування ![]() у хвилеводі.
у хвилеводі.
На рис.1.8.3 показано розташування складової ![]() у хвилеводі (б) та еп’юру залежності
її від координати х.
у хвилеводі (б) та еп’юру залежності
її від координати х.
На рис.1.8.4 показана структура поля (картина поля)
хвилі ![]() у поперечному (а) та повздовжньому
перерізах прямокутного хвилеводу.
у поперечному (а) та повздовжньому
перерізах прямокутного хвилеводу.
Оскільки повздовжнє хвильове число
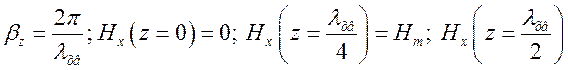
і т.д., що і видно з рис.1.8.1б і в.
Відповідно:
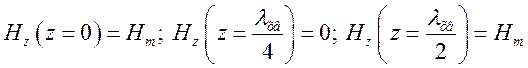
і т.д., (див. рис.1.8.2б і в)
Максимумів ![]() і нулів поперечна
складова
і нулів поперечна
складова ![]() досягає при таких самих значеннях, що
і поперечна складова
досягає при таких самих значеннях, що
і поперечна складова ![]() .
.
Аналогічно можуть бути визначені аналітичні вирази для строгої побудови картин поля будь-яких типів хвиль, які можуть існувати у прямокутному хвилеводі.
1.9 Нестрога методика побудови картин поля ![]() та
та ![]() у
прямокутному хвилеводі.
у
прямокутному хвилеводі.
Ця методика побудови картин поля носить нестрогий, а скоріше мнемонічний характер і будується на таких відомих положеннях:
1)
у хвиль електричного типу
магнітне поле розташоване тільки у поперечній площині; ці хвилі мають
повздовжну складову ![]() , орієнтовану вздовж хвилеводу;
, орієнтовану вздовж хвилеводу;
2)
у хвиль магнітного типу
електричне поле розташоване тільки у поперечній площині; ці хвилі мають
повздовжну складову ![]() , орієнтовану вздовж
хвилеводу;
, орієнтовану вздовж
хвилеводу;
3) біля поверхні ідеального металу не існує тангенціальна складова електричного поля; електричні силові лінії є перпендикулярними (нормальними) до поверхні металу;
4) магнітні силові лінії є замкнутими і підходять тангенціально до металу;
5) магнітні та електричні силові лінії у будь-якій точці поля є взаємно – перпендикулярними;
6) індекс m у типі хвилі показує кількість напівхвиль, що розміщуються між стінками хвилеводу у напрямку осі ОХ;
7) індекс n у типі хвилі показує кількість напівхвиль, що розміщуються між стінками хвилеводу у напрямку осі ОY.
Користуючись цими положеннями побудуємо картину поля
хвилі ![]() у прямокутному хвилеводі. Оскільки
магнітні хвилі мають лише поперечні складові електричного поля, тобто вони у
поперечному перетині хвилеводу зображаються у натуральну величину, слід
починати побудову саме з цієї проекції.
у прямокутному хвилеводі. Оскільки
магнітні хвилі мають лише поперечні складові електричного поля, тобто вони у
поперечному перетині хвилеводу зображаються у натуральну величину, слід
починати побудову саме з цієї проекції.
У хвилі ![]() є лише одна
електрична складова
є лише одна
електрична складова ![]() , яка вздовж сторони а
утворює одну напівхвилю, залишаючись перпендикулярною до верхньої і нижньої
стінок хвилеводу. Згідно з граничними умовами, вектор
, яка вздовж сторони а
утворює одну напівхвилю, залишаючись перпендикулярною до верхньої і нижньої
стінок хвилеводу. Згідно з граничними умовами, вектор ![]() має
дорівнювати нулю при
має
дорівнювати нулю при ![]() та
та ![]() ,
а, отже, буде мати максимальне значення посередині при
,
а, отже, буде мати максимальне значення посередині при 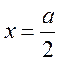 (рис.1.9.1).
(рис.1.9.1).
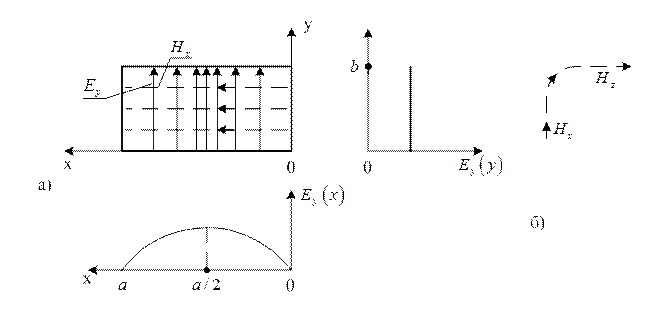
Рисунок 1.9.1
Вздовж напрямку OY
(вздовж сторони b) вектор ![]() залишається
незмінним. У цьому ж перетині хвилеводу будемо бачити і складову поля
залишається
незмінним. У цьому ж перетині хвилеводу будемо бачити і складову поля ![]() , яка має бути перпендикулярною до
, яка має бути перпендикулярною до ![]() (горизонтальною). Магнітні складові
поля будемо зображати штриховими лініями. Оскільки досліджувальна хвиля є
магнітною, вона має ще й повздовжню складову
(горизонтальною). Магнітні складові
поля будемо зображати штриховими лініями. Оскільки досліджувальна хвиля є
магнітною, вона має ще й повздовжню складову ![]() ,
у яку плавно має перейти поперечна складова
,
у яку плавно має перейти поперечна складова ![]() і
утворити разом замкнуту лінію. Цей перехід з утворенням замкнутої лінії
магнітного поля зображено на рис. 1.8.4б та рис. 1.9.1б.
і
утворити разом замкнуту лінію. Цей перехід з утворенням замкнутої лінії
магнітного поля зображено на рис. 1.8.4б та рис. 1.9.1б.
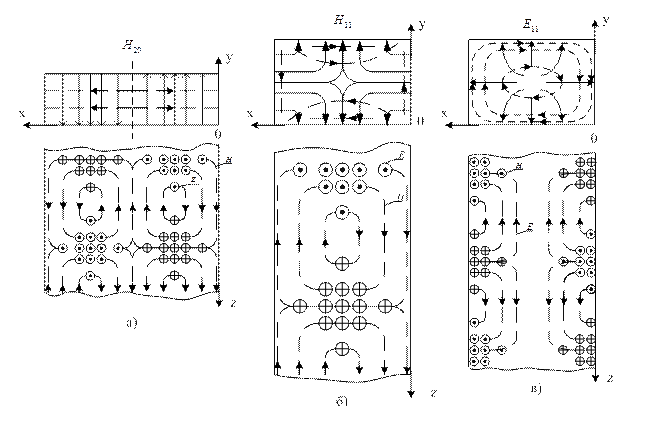
Рисунок 1.9.2
На рис. 1.9.2 показані картини полів декількох хвиль з
малими значеннями індексів m та n:
![]() . Нагадаємо, що починати побудову картини поля
будь-якої хвилі слід з поперечного перетину і для силових ліній тих складових,
які є лише поперечними. Тобто для
. Нагадаємо, що починати побудову картини поля
будь-якої хвилі слід з поперечного перетину і для силових ліній тих складових,
які є лише поперечними. Тобто для ![]() хвиль починають з
вектора
хвиль починають з
вектора ![]() , для
, для ![]() -
з вектора
-
з вектора ![]() .
.
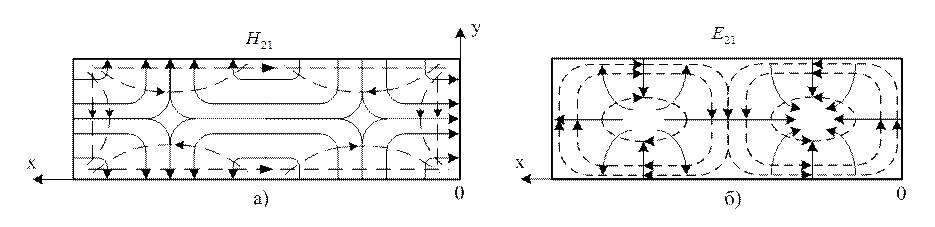
Рисунок 1.9.3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.