Електричну складову поля визначимо скориставшись першим рівнянням Максвелла при відсутності втрат, записаним у диференціальній формі:
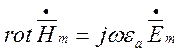 звідки
звідки 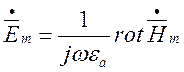 . (1.12.6)
. (1.12.6)
Скориставшись виразом для ![]() у циліндричній системі координат,
запишемо:
у циліндричній системі координат,
запишемо:
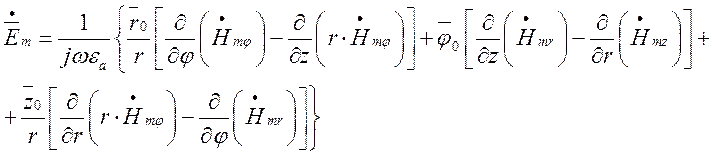
Оскільки 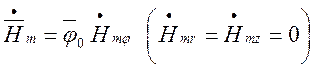 , останній вираз перепишеться так:
, останній вираз перепишеться так:
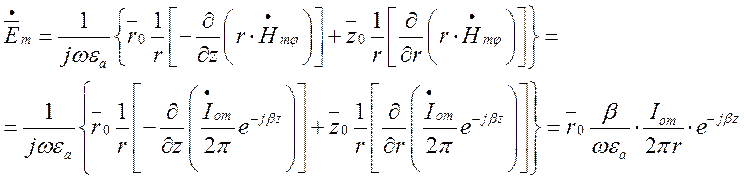 (1.12.7)
(1.12.7)
Відношення ![]() , пам’таючи що при відсутності втрат
, пам’таючи що при відсутності втрат ![]() , дорівнюватиме:
, дорівнюватиме:
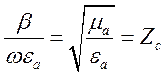 ,
,
де,
нагадаємо, ![]() - хвильовий опір середовища, яке
заповнює хвилевід.
- хвильовий опір середовища, яке
заповнює хвилевід.
З виразу (1.12.7) випливає, що у поля хвилі Т типу у коаксіальному хвилеводі є лише одна радіальна складова електричного поля:
![]() , де
, де 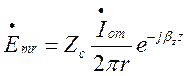 . (1.12.8)
. (1.12.8)
Для практики має велике
значення хвильовий опір круглого коаксіального хвилеводу з хвильою Т
типу. Під цим опором будемо розуміти відношення комплексної амплітуди напруги ![]() до комплексної амплітуди струму
до комплексної амплітуди струму ![]() у довільному перетині коаксіальної
лінії передачі.
у довільному перетині коаксіальної
лінії передачі.
Оскільки ![]() є напругою між зовнішнім провідником
(радіусом R) та внутрішнім провідником (радіусом r) , знаходимо її як інтеграл у межах
є напругою між зовнішнім провідником
(радіусом R) та внутрішнім провідником (радіусом r) , знаходимо її як інтеграл у межах ![]() від
від ![]() :
:
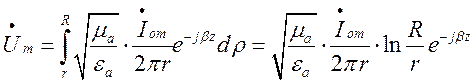 .
.
Тоді хвильовий опір
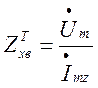 , або
, або 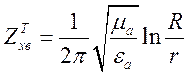 .
(1.12.9)
.
(1.12.9)
Якщо заповненням хвилеводу є
сухе атмосферне повітря ![]() , то вираз
(1.12.9) перепишеться так:
, то вираз
(1.12.9) перепишеться так:
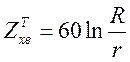 .
.
На практиці широко використовуються гнучкі круглі коаксіальні хвилеводи, які називаються коаксіальними кабелями. Ці кабелі випускаються промисловістю і мають хвильові опори: 50, 75, 100, 150…Ом. У побуті ми користуємося кабелями марки РК75 (75 Ом), наприклад, при з’єднанні приймальної антени з телевізором.
Вони представляють собою одно
– (багато) жильний внутрішній циліндричний провідник і циліндричну «плетенку» з
тонкого мідного дроту (зовнішній провідник, або екран), розділені
високочастотним полівініловим, наприклад, діелектриком, який дозволяє кабель
перегинати, що створює зручності при його використанні. Розрахувати його
хвильовий опір можна за формулою (1.12.9), поклавши ![]() (немагнітний
діелектрик) та
(немагнітний
діелектрик) та ![]() :
:
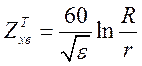 ,
,
де ![]() - відносна діелектрична проникність
діелектрика.
- відносна діелектрична проникність
діелектрика.
1.13 Діелектричний хвилевід
За приклад такого хвилеводу
візьмемо нескінченно - довгий, круглий циліндричний стрижень радіусом R, виготовлений з діелектрика з параметрами ![]() ;
; ![]() , і, який знаходиться у необмеженому
середовищі з параметрами
, і, який знаходиться у необмеженому
середовищі з параметрами ![]() (на практиці це
сухе повітря). Аналіз будемо проводити у циліндричній системі координат
(рис.1.13.1)
(на практиці це
сухе повітря). Аналіз будемо проводити у циліндричній системі координат
(рис.1.13.1)
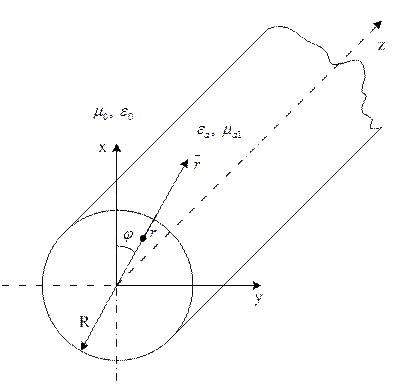
Рисунок 1.13.1
Вирази для повздовжних
складових ![]() та
та ![]() повинні
задовольняти рівнянням Гельмгольця для полів які в середині стрижня, так і у
оточуючому його середовищі. Для поля в середині стрижня такими рівняннями є:
повинні
задовольняти рівнянням Гельмгольця для полів які в середині стрижня, так і у
оточуючому його середовищі. Для поля в середині стрижня такими рівняннями є:
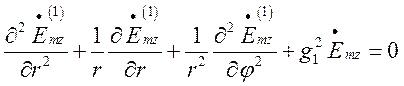 (1.13.1)
(1.13.1)
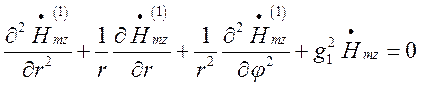 (1.13.2)
(1.13.2)
Де поперечне хвильове число ![]() (1.13.3)
(1.13.3)
Для поля у оточуючому середовищі:
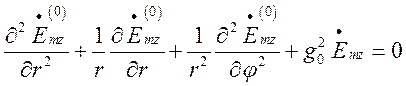 (1.13.4)
(1.13.4)
![]()
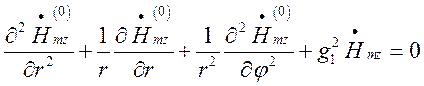 (1.13.5)
(1.13.5)
Де поперечне хвильове число ![]() (1.13.6)
(1.13.6)
Загальними розв’язками рівнянь (1.13.1) та (1.13.2) є функції, які збігаються за конструкціями з функціями (1.10.9) та (1.10.19) а саме:
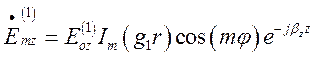 (1.13.7)
(1.13.7)
та 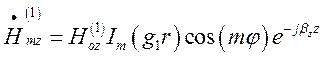 (1.13.8)
(1.13.8)
Пока циліндром, де структура
поля відповідає структурі поверхневої хвилі, амплітуди полів мають зменшуватись
експоненціально у напрямку від бічної поверхні стрижня. Цій вимозі
задовольняють функції Ханкеля другого роду від чисто уявного аргументу ![]() ,
, ![]()
![]() .
.
Тому розв’язки рівнянь (1.13.3) та (1.13.4) слід записати у такому вигляді:
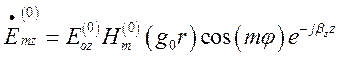 (1.13.9)
(1.13.9)
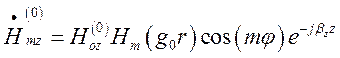 (1.13.10)
(1.13.10)
Поперечні складові електричного і магнітного полів визначимо підстановкою (1.13.5) - (1.13.8) в співвідношення (1.4.11) – (1.4.14); у тілі діелектричного стрижня:
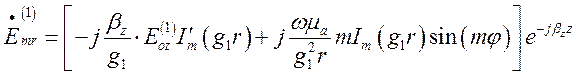 (1.13.11)
(1.13.11)
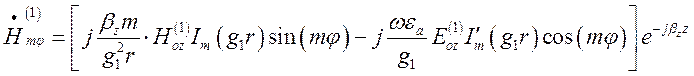 (1.13.12)
(1.13.12)
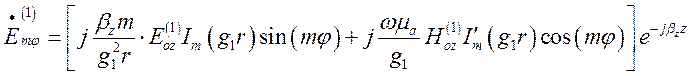 (1.13.13)
(1.13.13)
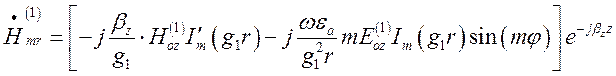 (1.13.14)
(1.13.14)
поза діелектриком:
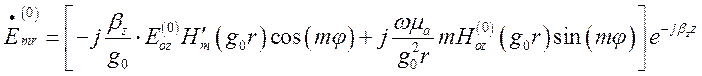 (1.13.15)
(1.13.15)
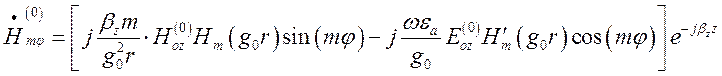 (1.13.16)
(1.13.16)
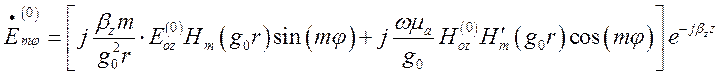 (1.13.17)
(1.13.17)
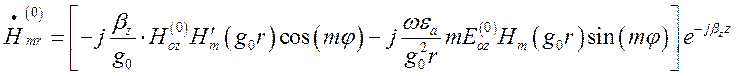 (1.13.18)
(1.13.18)
На межі розділу двох
середовищ ![]() тангенціальні складові електричного
і магнітного полів мають бути неперервними, чому відповідатиме запис:
тангенціальні складові електричного
і магнітного полів мають бути неперервними, чому відповідатиме запис:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.