Об’ємні резонатори. Прямокутний об’ємний резонатор. Циліндричний круглий об’ємний резонатор. Картини полів у об’ємних резонаторах

2 ОБ’ЄМНІ РЕЗОНАТОРИ

2.1 Загальні зауваження

У радіотехніці на відносно низьких частотах, які не перевищують 50 МГц, коливальні контури (резонатори) складаються з конденсаторів та котушок індуктивності. Коливальний процес у таких резонаторах за змістом є процес обміну енергіями між  електричним полем зарядженого конденсатора і магнітним полем “зарядженої” котушки.

На більш високих частотах котушки і конденсатори мають такі великі втрати, що коливальний контур стає дуже низько добротним і не може виконувати своєї основної функції – бути вибірною системою. Таку задачу у діапазоні до 300 МГц можуть успішно виконувати резонатори, які представляють собою відрізки двопровідної лінії передачі електромагнітної енергії. Так, наприклад, відомо, що короткозамкнутий відрізок такої лінії еквівалентний паралельному коливальному контуру, розімкнутий на кінці відрізок – послідовному контуру.

 Двопровідні лінії передачі і побудовані на їх основі резонатори є ефективними тоді, коли відстань між провідниками лінії є набагато меншою за довжину хвилі. Тому на частотах близьких до 300 МГц і більших ( практично до 3 ГГц) ефективними є резонатори, побудовані на базі коаксіальних круглих хвилеводів з хвилями T типу. На більших частотах втрати у коаксіальних хвилеводах ( та і резонаторах) зростають, що обмежує діапазон їх використання. В діапазоні НВЧ ( 3…30 ГГц) та у діапазоні міліметрових хвиль ( 30…300 ГГц) широко використовуються  резонатори на базі прямокутних та круглих циліндричних хвилеводах. Але такі системи втрачають свою ефективність на субміліметрових і більш коротких хвилях через дуже малі розміри хвилеводів. Через це основою для побудови такого резонатора може слугувати, наприклад, відрізок діелектричного хвилеводу циліндричної форми, металізованого на обох його торцях. При подальшому скороченні робочої довжини хвилі переходять до резонаторів відкритого типу, подібних до пристроїв оптичного діапазону.

          У кожному зі згаданих випадків поле зосереджене у об’ємі без втрат. Через це такі системи отримали назву  об’ємних резонаторів.

          Зауважимо, що у даній частині навчального посібника будуть розглядатися об’ємні резонатори, побудовані на базі регулярних без втрат хвилеводів. Таке спрощення задачі дозволить зосередити увагу читачів на визначенні складових полів коливань в резонаторах, побудові структур полів коливань різних типів, визначенні резонансних частот ( довжин хвиль).

          Такі питання як втрати та добротності об’ємних резонаторів доцільно розглядати у курсі  “Пристрої НВЧ та антени”.

2.2 ПРЯМОКУТНИЙ ОБ’ЄМНИЙ РЕЗОНАТОР

Прямокутний об’ємний резонатор є відрізок прямокутного хвилеводу, який має ще дві поперечні металеві стінки (рис.2.2.1). Тобто мова йде про прямокутний паралелепіпед з поперечними розміра a,в  та довжиною l, розміщений у прямокутній системі координат.

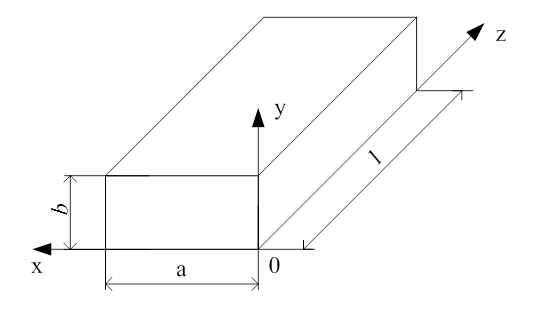
Рисунок 2.2.1

2.2.1 Коливання Е-типу

Насамперед поставимо задачу визначення складових поля коливань Е-типу у прямокутному резонаторі. Міркуватимемо так: у прямокутному хвилеводі вздовж осі OZ поширюється хвиля типу  (падаюча хвиля), складові поля якої представлені виразами (1.7.11). Для зручності подальшого аналізу перепишемо їх; і, отже, для падаючої (прямої) хвилі:

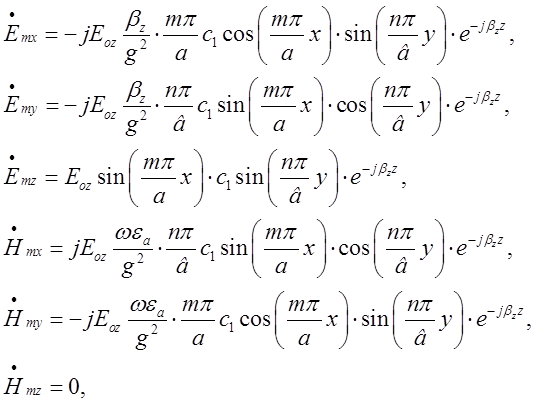
де  - амплітудний множник прямої (падаючої) хвилі типу .

Досягнувши задньої поперечної стінки, ця хвиля відіб’ється і буде рухатися у напрямку осі – OZ (відбита хвиля). Приріст її фази на одиниці довжини шляху у додатньому напрямку осі OZ буде від’ємним, тобто для відбитої хвилі повздовжнє хвильове число слід брати зі знаком мінус .

Отже вирази для складових поля у відбитій хвилі легко отримати з виразів для падаючої хвилі, замінивши скрізь  на :

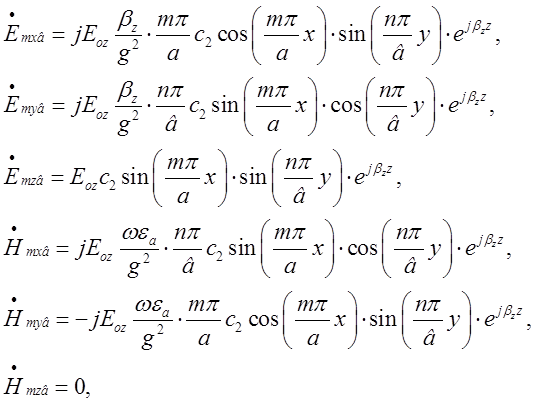
де  - амплітудний множник відбитої хвилі типу .

У результаті інтерференції цих двох хвиль утвориться результуюче коливання у закритому об’ємі прямокутного резонатора.

Щоб знайти складові поля цього коливання, достатньо скласти між собою відповідні складові падаючої та відбитої хвиль.

Виконавши додавання, отримаємо:

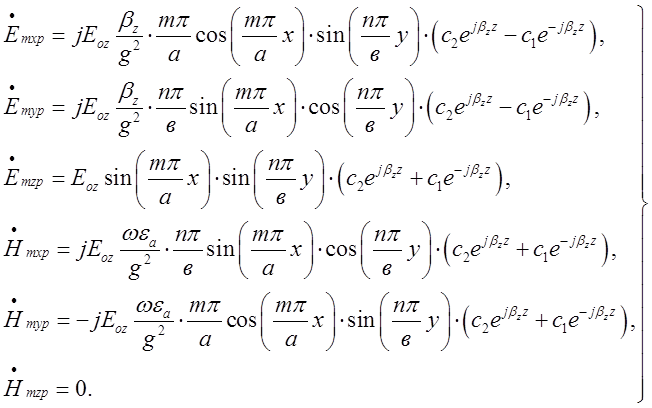          (2.2.1)

Відзначимося з амплітудними коефіцієнтами  та , для чого скористаємося граничними умовами для тангенціальних складових електричного поля на ідеальному провіднику:  

У резонаторі такими складовими (дотичними до поперечних стінок резонатора при  та ) є  та .

Прирівнявши, наприклад, до нуля при , матимемо:

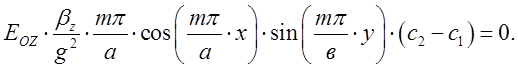
Оскільки ця рівність має бути справедливою при усіх значеннях поперечних координат  на передній стінці резонатора, то висновок може бути лише такий : = 0 або . Покладемо ( повне відбиття).