Об’ємні резонатори. Прямокутний об’ємний резонатор. Циліндричний круглий об’ємний резонатор. Картини полів у об’ємних резонаторах, страница 2

З урахуванням сказаного, множники в круглих дужках  виразів (2.2.1) за формулами Ейлера перепишуться так:

Таким чином вирази (2.2.1) матимуть вигляд;

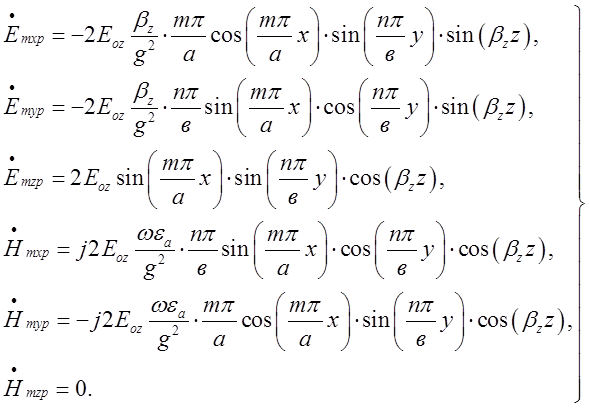         (2.2.2)        

Визначимося з повздовжним хвильовим числом , а для цього скористаємось тим, що, наприклад,  при  (задня поперечна стінка резонатора), тобто:

.

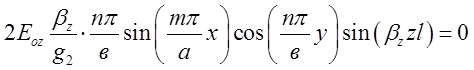Ця рівність має бути справедливою для усіх координат  та  на вибраній стінці резонатора. Звідки:

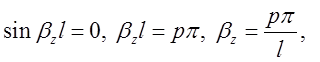                         (2.2.3)

де р=0,1,2,3...

Підставивши (2.2.3) в (2.2.2), отримаємо остаточні вирази для комплексних амплітуд складових векторів поля коливання типу  у прямокутному резонаторі:

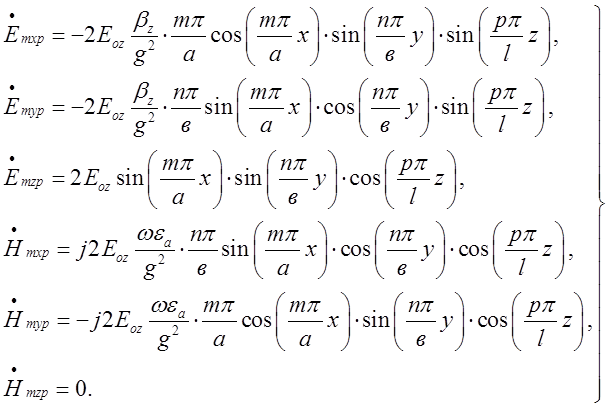           (2.2.4)         

Третій індекс р, аналогічно до індексів  та , вказують на кількість на півхвиль, які розміщуються на довжині резонатора .

З виразів (2.2.4) видно, що вздовж резонатора, так само як і у поперечних напрямках, установлюється стійна хвиля. Третій індекс р може дорівнювати нулю, і при цьому у резонаторі будуть коливання типу  зі складовими  Так само як і у прямокутному хвилеводі, індекси  та дорівнювати нулю не можуть, тобто коливання типу  та  - не можливі.

Знайдемо вирази для резонансної частоти (довжини хвилі) об’ємного резонатора з коливаннями типу.

Згадаємо, що вираз для сталої поширення , на резонансній частоті буде таким: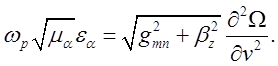

Звідки:

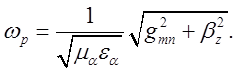
З урахуванням того, що , виразів (1.7.8), (1.7.9) та (2.2.3) формула для  перепишеться так:

,

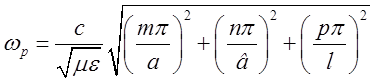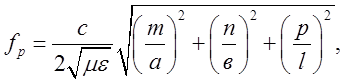                                                    (2.2.5)                               

де  - параметри середовища, яким заповнений резонатор, м/с – швидкість світла у вакуумі.

При заповненні об’ємного резонатора сухим повітрям:

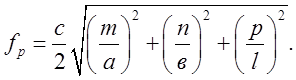                              (2.2.6)

Відповідно, резонансна довжина хвилі у об’ємному резонаторі дорівнюватиме:

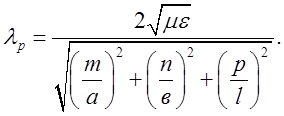                                        (2.2.7)

Або при заповнені сухим повітрям:

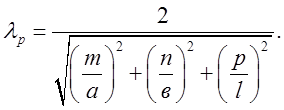                                                   (2.2.8)

2.2.2 КОЛИВАННЯ Н- типу

Складові поля падаючої хвилі типу  представлені виразом ( 1.7.16). Для зручності подальшого аналізу перепишемо його :

,

 ,

                      ,

,

 ,

                     .

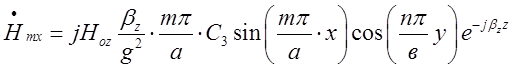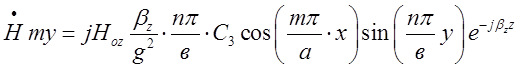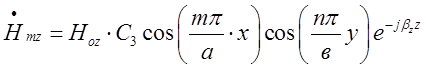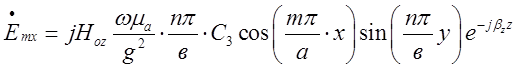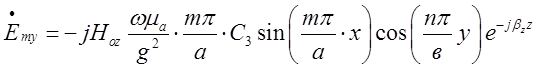Для відбитої хвилі, замінивши скрізь , будемо мати:

                      ,

                      ,

                      ,

                      ,

                      ,

                      .

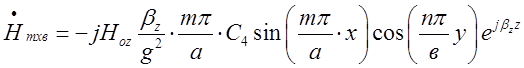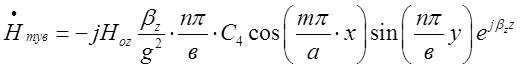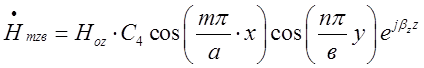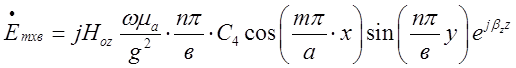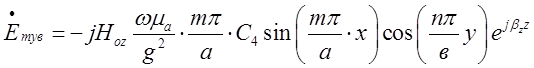У результаті інтерференції утвориться коливання у резонаторі, складові поля якого будуть дорівнювати:

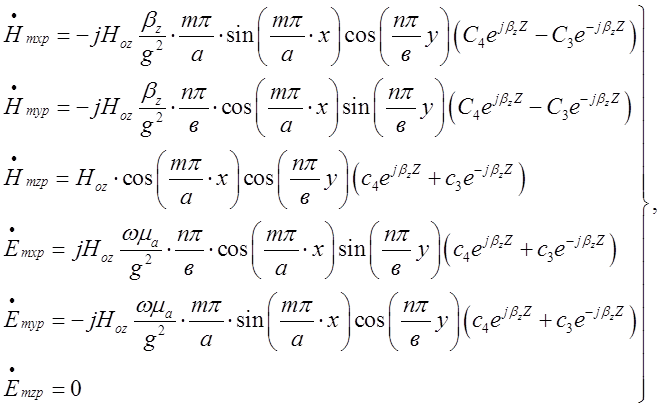       (2.2.9)    

звідки .

Поклавши  вирази для складових поля у резонаторі, з урахуванням формул Ейлера, перепишуться таким чином:

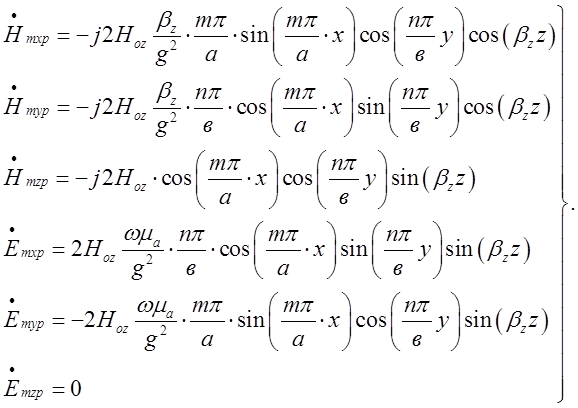           (2.2.10)       

Ця сама складова поля  у  резонаторі, будучи тангенціальною (дотичною) до задньої поперечної стінки (, дорівнює нулю:

,

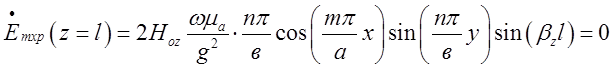звідки

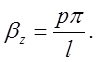                                               ( 2.2.11)

З урахуванням ( 2.2.11) вираз (2.2.10) перепишемо так:

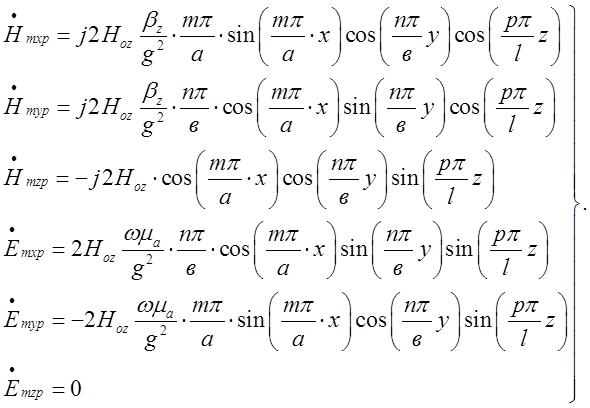        ( 2.2.12)

З виразів (2.2.12)  видно, що третій індекс у коливаннях типу  не може дорівнювати нулю ( коливання типу  не можливе), бо зникають усі ще й поперечні складові електричного поля.

Резонансна частота , та резонансна довжина хвилі можуть бути визначеними за формулами (2.2.5) та (2.2.8) відповідно, оскільки вирази для  залишаються такими самими як і у випадку коливань типу .

2.3 ЦИЛІНДРИЧНИЙ КРУГЛИЙ ОБ’ЄМНИЙ РЕЗОНАТОР

Циліндричний круглий об’ємний резонатор представляє собою відрізок циліндричного круглого хвилеводу, закритого з обох торців провідними стінками (рис.2.3.1).

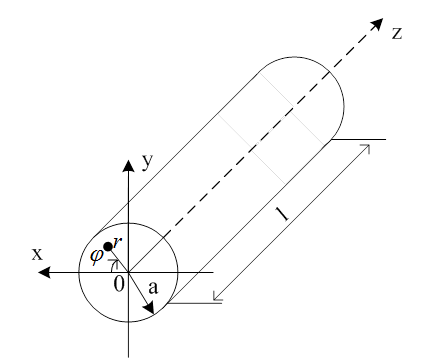
Рисунок 2.3.1

Тобто мова йде про закритий об’єм, обмежений повною поверхньою круглого циліндра з радіусом основи а та довжиною l, розміщений у циліндричній системі координат .

2.3.1 КОЛИВАННЯ Е- типу

Будемо вважати основною задачою цього  підрозділу визначення виразів для складових поля коливань типу . За аналогією з попередніми випадками вважатимемо, що вздовж осі  поширюється падаюча хвиля типу  зі складовими поля (див. випадок хвилі Е –типу у циліндричному хвилеводі):

                     ,

                     ,

                     ,

                     ,

                     ,

                     .

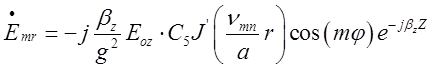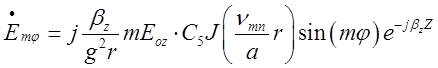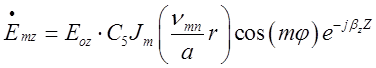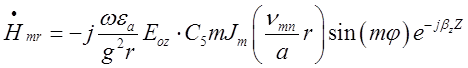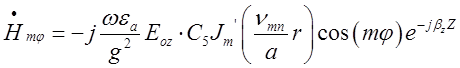Вирази для відповідних складових відбитої хвилі будуть такими:

                       

                       

                       

                       

                       

                        .

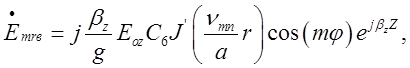
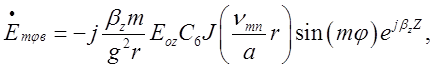
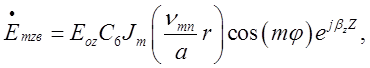
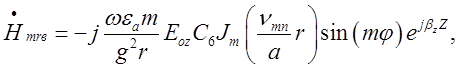
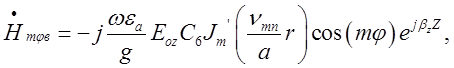
В об’ємному резонаторі:

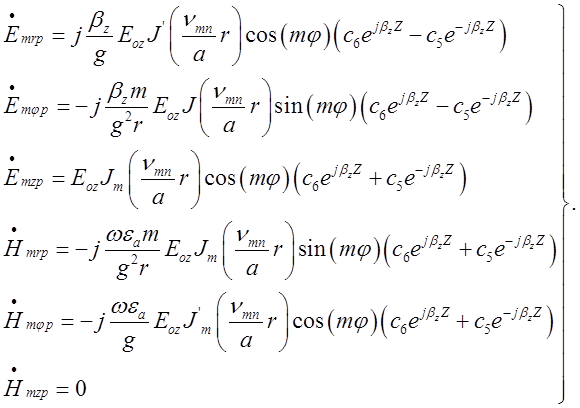            (2.3.1)          

При  складова а отже:

Тоді вирази (2.3.1), з урахуванням формул Ейлера, можна переписати таким чином: