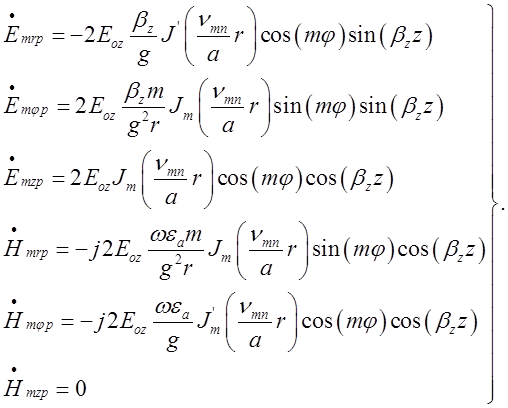Об’ємні резонатори. Прямокутний об’ємний резонатор. Циліндричний круглий об’ємний резонатор. Картини полів у об’ємних резонаторах, страница 3

                 (2.3.2)     

При складова а отже

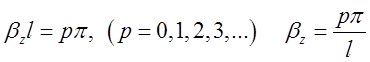.                     (2.3.3)

Підставивши в (2.3.2) вираз для  (2.3.3) матимемо остаточні вирази для комплексних амплітуд складових поля коливань типу  у циліндричному резонаторі:

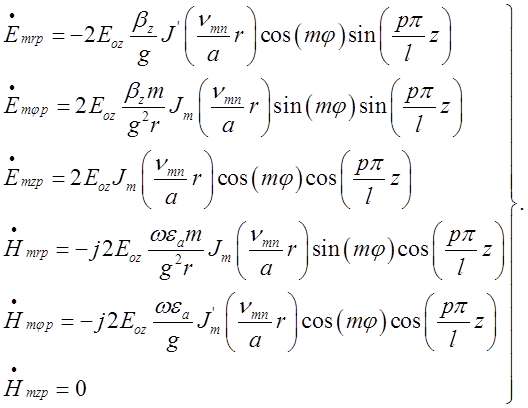                   (2.3.4)  

Формулу для визначення резонансної частоти коливань типу  у циліндричному резонаторі знайдемо з виразу:

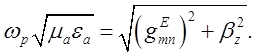
Оскільки поперечне хвильове число для хвиль  типу   ,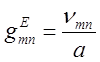

резонансна частота  дорівнюватиме:

                                  ,

                                  ,

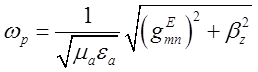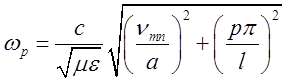або

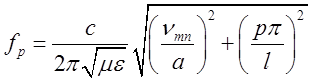                                 ,                              (2.3.5)         

При заповненні резонатора сухим атмосферним повітрям:

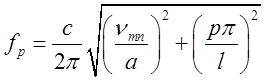.                                   (2.3.6)

Резонансна довжина хвилі дорівнюватиме:

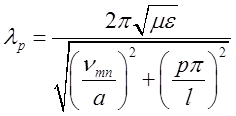,                                    (2.3.7)

або ( при повітряному заповненні):

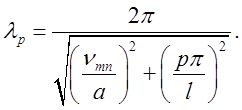                                     (2.3.8)

2.3.2 КОЛИВАННЯ Н – типу

Діючи за аналогією до попереднього випадку, запишемо складові поля хвилі типу , яка поширюється вздовж осі OZ круглого циліндричного хвилеводу (падаючої хвилі):

                     

                     

                     

                     

                     

                     

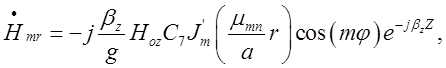
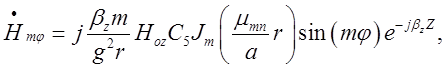
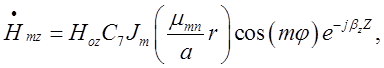
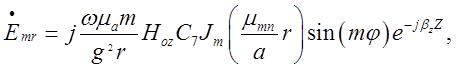
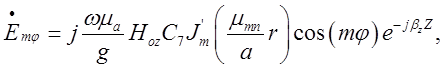
Складові поля відбитої хвилі будуть такими:

                      ,

                     ,

                     ,

                     ,

                     ,

                    

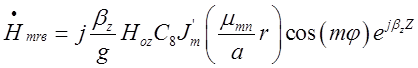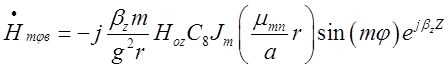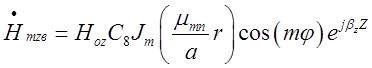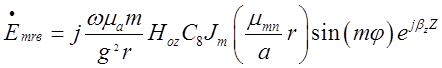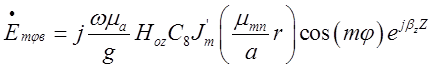Складові поля коливання типу  у круглому циліндричному резонаторі дорівнюватимуть:

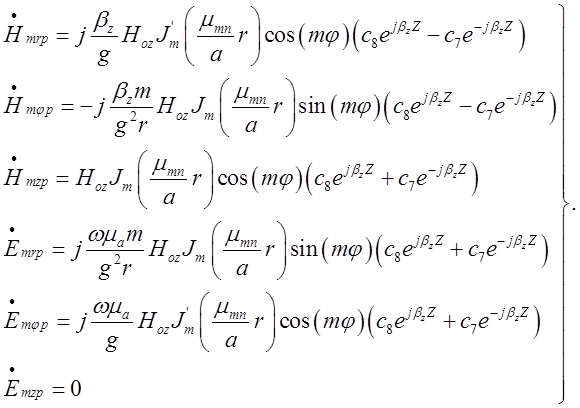            (2.3.9)          

При.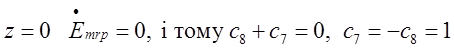

З урахуванням формул Ейлера:

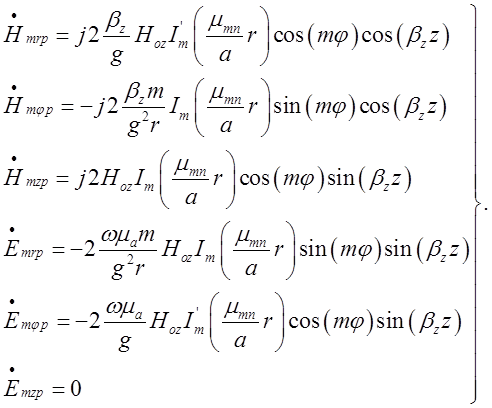                     (2.3.10)        

При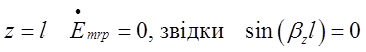

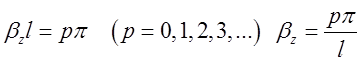.                           (2.3.11)

З урахуванням (3.2.1) вираз (3.2.10) перепишеться так:

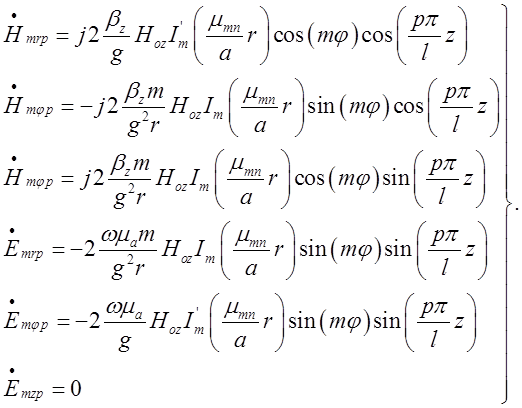             (2.3.12)                

Резонансна частота  дорівнюватиме:

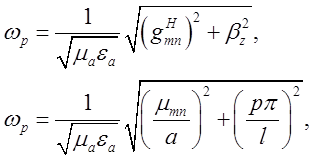
або

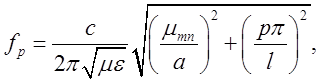                         (2.3.13)

при заповненні резонатора сухим атмосферним повітрям:

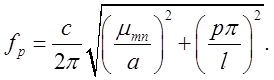                                (2.3.14)

Резонансна довжина хвилі:

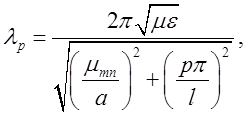                                     (2.3.15)

або (при повітряному заповненні)

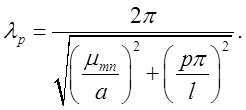                                      (2.3.16)

2.4 КОАКСІАЛЬНИЙ ОБ’ЄМНИЙ РЕЗОНАТОР

Під коаксіальним об’ємним резонатором будемо розуміти відрізок коаксіального хвилеводу довжиною , закритого з обох сторін поперечними провідними стінками. Будемо також вважати, що у коаксіальному хвилеводі існує хвиля типу. Щоб визначити складові поля коливання типу  у коаксіальному об’ємному резонаторі (рис.2.4.1), скористуємося складовими поля хвилітипу, яка поширюється у напрямку осі (падаюча хвиля):

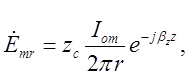
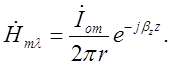
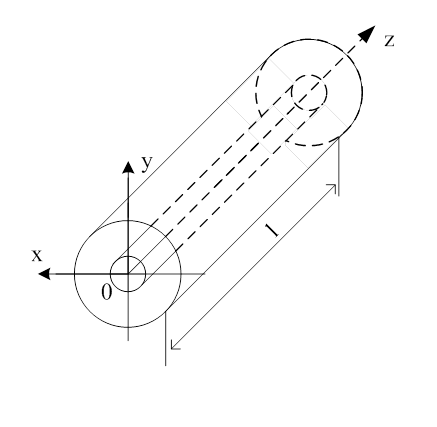
Рисунок 2.4.1

При визначенні складових полів у відбитій хвилі потрібно поміняти на протилежний знак перед та враховувати граничні умови на торцях резонатора для тангенціальних  складових векторів поля.Так, наприклад, при :

;

звідки 

.

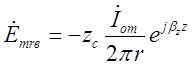Оскільки тангенціальна складова магнітного поля  на торцовій стінці резонатора не дорівнює нулю, то:

.

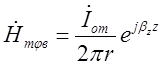Склавши відповідні складові, отримаємо:

                             ,

                            .

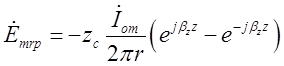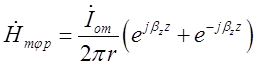З урахуванням формул Ейлера:

                                     ,

                                      .

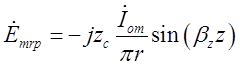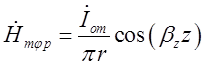Як відомо, при z=l складова  має дорівнювати нулю. Звідки   ( p=0,1,2,3,…) . Тоді вирази для складових поля коливання типу  у коаксіальному резонаторі перепишуться так:

                                  

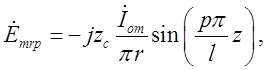
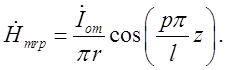                                        ( 2.4.1)

де, нагадаємо, p- показує, яка кількість напівхвиль міститься на довжині резонатора l.

Тобто при резонансі на довжині  вкладається штук на півхвиль. Через це такі резонатори називаються напівхвильовими.

Як відомо, у коаксіальному хвилеводі з хвилею  дисперсія відсутня, а отже резонансна довжина хвилі

                                        ( 2.4.2 )

Резонансна частота:

                                     ( 2.4.3 )

Прі повітряному заповненні резонатора:

                                               ( 2.4.4 )

                                             ( 2.4.5 )

При заданій довжині хвилі або частоті коливання, резонанс наступить при довжині резонатора :

                                        ( 2.4.6 )

                                       ( 2.4.7 )

Або при повітряному заповненні:

                                                 ( 2.4.8 )

                                             ( 2.4.9 )

2.5 УМОВИ ІСНУВАННЯ В ОБ’ЄМНИХ РЕЗОНАТОРАХ

КОЛИВАНЬ ЗАДАНОГО ТИПУ