Об’ємні резонатори. Прямокутний об’ємний резонатор. Циліндричний круглий об’ємний резонатор. Картини полів у об’ємних резонаторах, страница 4

Раніше наголошувалось, що об’ємний резонатор представляє собою відрізок хвилеводу довжиною , замкнутого з обох торців металевими площинами. Отже, умова існування коливання заданого типу перш за все визначається можливістю поширення відповідної хвилі у хвилеводі, на базі якого виготовлений резонатор. Нагадаємо, що оскільки у резонаторі , то у прямокутному резонаторі умова існування коливань типу  чи  має бути такою :

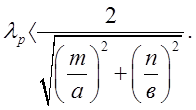                                      ( 2.5.1 )

Знайдемо умову, яка визначає довжину прямокутного резонатора , при якій можливе існування коливань типу . У випадках, коли , при заданих розмірах а і в та резонансної довжини хвилі , довжину резонатора визначемо за формулою:

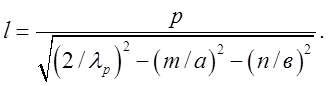                            ( 2.5.2 )

У випадку, коли  ( коливання типу ) така умова не існує, бо резонансна довжина хвилі не залежить від довжини резонатора , і залишається лише умова:

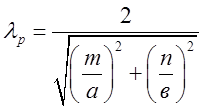.                                     ( 2.5.3 )

Щодо  круглого циліндричного резонатора, то при  умовами існування коливань будуть такі:

для коливань електричного типу

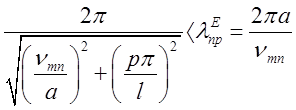,                            ( 2.5.4 )

для коливань магнітного типу

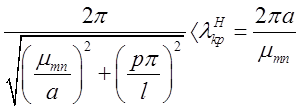.                           ( 2.5.5 )

При  у випадку коливань електричного типу нерівності ( 2.5.4 ) і ( 2.5.5 ) переходять у рівності.

2.6 КАРТИНИ ПОЛІВ У ОБ’ЄМНИХ РЕЗОНАТОРАХ

Як видно з виразів для складових полів хвиль у хвилеводах та коливань відповідних типів у відповідних резонаторах, у поперечних перетинах ці картини повністю збігаються. У повздовжніх перетинах є суттєві відмінності. Якщо у хвилеводах поперечні складові векторів збігаються за фазами як гармонічні функції повздовжньої координати , то у резонаторах вони взаємно зміщені у просторі вздовж осі на .

Приклад 1. Картини полів хвилі  у прямокутному хвилеводі (рис. 2.6.1,а) та коливань  у прямокутному резонаторі (рис. 2.6.1,б) будуть такими:

                      а)                                                                 б)

Рисунок 2.6.1

У хвилеводі поперечна складова  як функція координати  досягає максимуму у тих самих точках, що і поперечна складова .

У об’ємному резонаторі ці максимуми вздовж хвилеводу зсунуті на . Тобто вздовж хвилеводу установлюється стійна хвиля довжиною  ( дві напівхвилі).

Приклад 2. Картини полів хвилі типу  у круглому циліндричному хвилеводі (рис. 2.6.2,а) та коливання типу  у відповідному резонаторі (рис. 2.6.2,б) будуть такими:

                                а)                                                б)

Рисунок 2.6.2

Приклад 3. Серед коливань  типу у прямокутному та циліндричному резонаторах можливі коливання типу  ( третій індекс ), коли довжина резонатора  буде меншою за половину довжини хвилі у відповідному хвилеводі. На рисунку 2.6.3 зображено картину поля коливання типу  у циліндричному об’ємному резонаторі.

Аналогічна картина поля має місце і у прямокутному резонаторі.

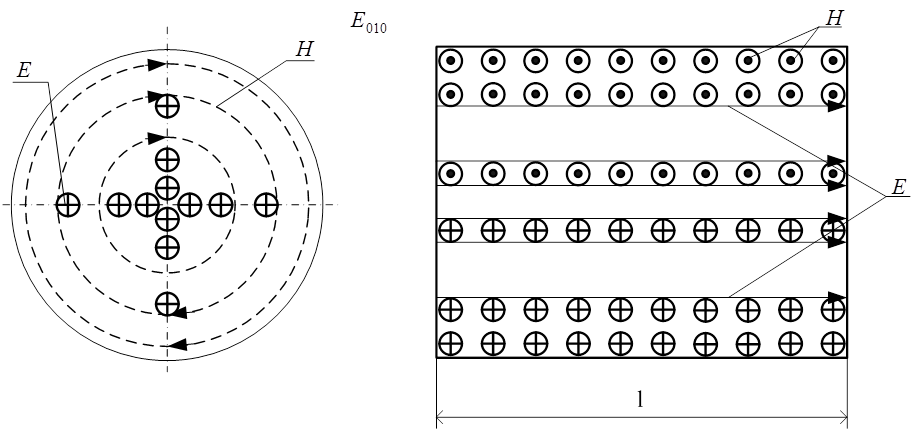
Рисунок 2.6.3

Практичний інтерес має коаксіальний об’ємний резонатор, створений на базі коаксіального хвилеводу з хвилею типу . Такі резонатори поширені у діапазоні дециметрових хвиль та короткій частині метрових хвиль.

Розглянемо варіант схеми конструкції напівхвильового  об’ємного коаксіального резонатора, зображеного на рис.2.4.1. У такому резонаторі можливі коливання типу . Як приклад, наведемо картину поля у напівхвильовому коаксіальному резонаторі з коливанням типу  ( рис.2.6.4).

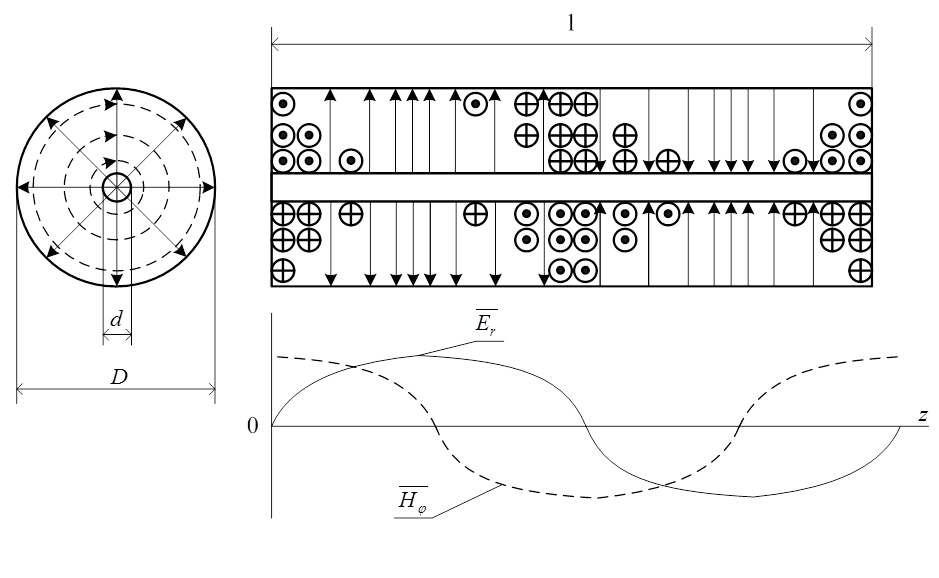Рисунок 2.6.4

На практиці використовується також коаксіальний об’ємний резонатор з зосередженою ємністю (рис.2.6.5). Така система може розглядатися як паралельний коливальний контур,

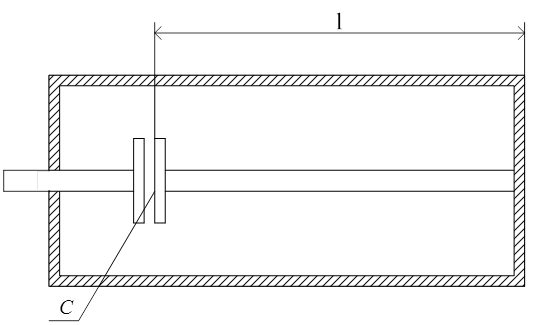
Рисунок 2.6.5

Де коаксіальний резонатор довжиною  виконує роль індуктивності, яка разом з конденсатором  утворює коливальний контур.

Частоту власних коливань такого контуру визначають за допомогою відомого співвідношення :

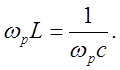
Якщо потрібно визначити ємність С , яка необхідна для отримання заданої резонансної частоти , то  слід скористатися формулою

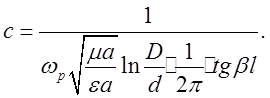
У випадку, коли резонатор заповнений сухим повітрям, то

,

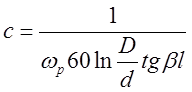де .

Картина поля у такому резонаторі представлена на рис.2.6.6.

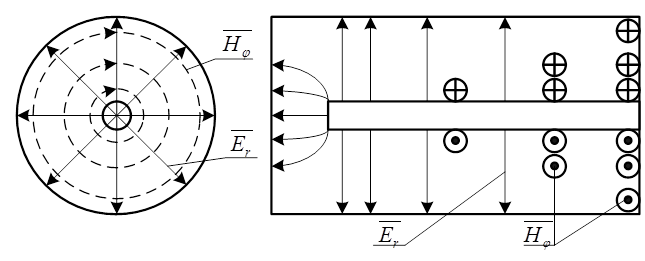
Рисунок 2.6.6

Резонансна довжина такого резонатора, як бачимо на рис.2.6.6, дорівнює приблизно чверті довжини хвилі генератора. Тому такі резонатори ( довжина їх кратна ) називаються чверть хвильовими.

2.7 РЕЗОНАТОРИ НВЧ ІНТЕГРАЛЬНИХ СХЕМ

В інтегральних схемах НВЧ генераторів, підсилювачів, фільтрів використовуються друковані та об’ємні резонатори.