2. Решение уравнений для получения промежуточных значений скорости
u*, v*, w*.
3. Решение дискретных аналогов уравнений для получения k, e и уравнений для Ym и h, ER.
4. Определение эффективной вязкости и расчет термодинамического состояния среды.
5. Решение уравнения для поправки давления p¢ и корректировка поля давления p= p*+p¢.
6. Вычисление поправок скорости и коррекция компонент скорости.
7. Расчет движения частиц.
8. Если условие сходимости не выполнено, то возврат на п. 2, пока не будет достигнута сходимость
.
4. Граничные условия.
4.1. Вход
В пакете “sFlow” существует возможность задавать на входе либо фиксированное значение скорости, либо массовый расход. При этом если задан расход то компоненты скорости u, v, w в каждом входе рассчитываются по заданному массовому расходу, углу наклона оси входного потока к осям координат и по доли потока, заданное для данного входного «окна». Например, компонента u на входе определяется следующим образом
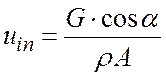(4.1.1)
где G - массовый расход жидкости на входе, r - суммарная плотность,
А-площадь сечения входного окна, a - угол между осью OX и осью входного
потока.
Кинетическая энергия турбулентности k и скорость диссипации турбулентности e на входе оцениваются по соотношениям вида:
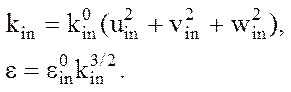(4.1.1)
где константы koin, eoin подбираются эмпирически.
Обычно для развитых турбулентных потоков на входе уровень турбулентных пульсации состовляет порядка 1%, поэтому koin=0,01, а eoin =Cm/L, где L - характерный размер энергосодержащих вихрей.
Энтальпия на входе вычисляется по заданным температуре входа и составу газов или жидкости.
Граничные условия для 
задаются в виде массовых долей
компонентов на входе.
4.2. Выход
На выходной границе при решении уравнений для u, v, w, k, e, h ставятся условия отсутствия градиентов (так называемые «мягкие условия»):
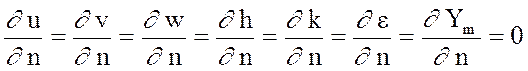, (4.2.1)
где n - вектор внешней нормали к расчетной области.
4.3. Симметрия (скольжение)
На плоскости симметрии
ставятся условия равенства нулю: производной по нормали к плоскости симметрии всех
скалярных величин 
и тангенциальной
состовляющей скорости 
, нормальной к плоскости состовляющая
скорости 
.
, 
,
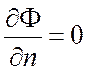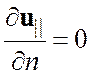(4.3.1)
где n- вектор нормали к плоскости симметрии.
4.4.Твердая стенка
Нормальную и тангенциальную компоненты скорости на стенках полагаем равными нулю, что моделирует соответственно непротекание и прилипание.
, 
(4.4.1)
Для определения турбулентных характеристик вблизи стенки используется метод пристеночных функций (смотри пункт 2.3).
Для массовых долей задаются условия отсутствия диффузионных потоков через стенку (конвективные потоки отсутствуют в силу (4.4.1))
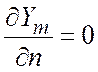(4.4.2)
где n- вектор нормали к стенки.
4.4.1. Теплоотдача на стенках
Граничные условия для уравнения на энтальпию можно задать двумя способами:
1.Задание постоянной температуры на стенке
(4.4.1.1)
2.Задание теплового потока и теплоотдачи на стенке
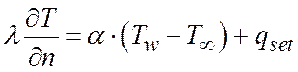(4.4.1.2)
где 
-
температура на стенке, 
- заданная
температура, 
- температура внешней среды, 
-заданный тепловой поток через
стенку, 
-коэффициент теплоотдачи.
5. Методы решения систем линейных алгебраических уравнений
После дискретизации исходных уравнении по времени и пространству получаем системы линейных алгебраических уравнений вида 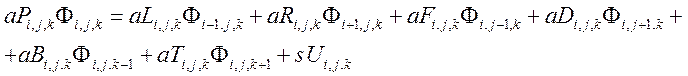(5.1)
(5.1)
Для решения систем линейных алгебраических уравнений в пакете реализовано несколько методов, описание которых можно найти в соответствующей литературе:
· полинейный (ADI) [12],
· переменных направлений (ADIM) [2],
· неполной факторизации Булеева (BM) [13],
· метод сопряженных невязок с факторизацией по Булееву (BMCRM).
6. Примеры и тесты
6.1. Ламинарное течение жидкости в плоской каверне.
6.2. Ламинарное двумерное течение жидкости за обратным уступом.
6.3. Ламинарное течение жидкости в гибе квадратного сечения.
6.4. Ламинарное обтекание цилиндра.
6.5. Ламинарное течение жидкости в тройнике.
6.6. Свободная конвекция в пространстве между двумя коаксиальными цилиндрами.
6.7. Свободная конвекция и радиационный теплообмен в квадратной полости.
6.8. Турбулентная свободная конвекция в вытянутой каверне.
6.9. Турбулентный теплообмен в расширяющемся канале.
6. Примеры и тесты
6.1. Ламинарное течение жидкости в плоской каверне
Тестирование реализованных в “sFlow” схем аппроксимации конвективных потоков проводилось на задаче о стационарном ламинарном течении вязкой несжимаемой жидкости в двумерной каверне.
Каверна (рисунок 1) представляет собой квадратную полость, верхняя стенка которой движется с постоянной скорость U=1м/с.
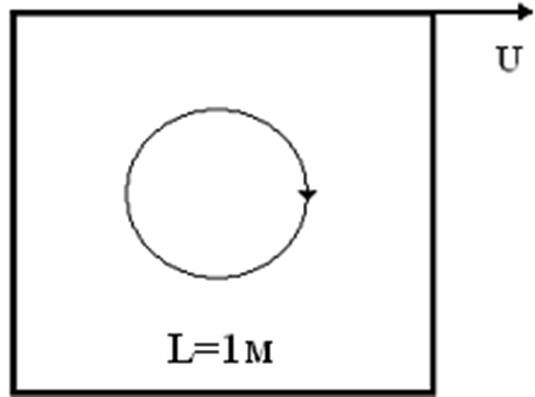
Рис 1. - Двумерная каверна
Граничные условия: на боковых и нижней стенках ставились условия непротекания и прилипания, на верхней стенке X компонента скорости задавалась равной 1 м/с, на торцах расчетной области ставились условия симметрии.
Плотность жидкости считалась равной единице, вязкость определялась по числу Рейнольдса.
Расчеты проводились на различных сетках 31×31, 41×41, 51×51, 61×61, равномерных и со сгущением, одна из них представлена на рисунке 2.
Исследование свойств схем
аппроксимации проводилось в широком диапазоне чисел Рейнольдса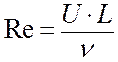 
. В качестве эталонного решения
задачи использовалось решение, полученное при помощи схемы QUIСKM на сетке 251×251 со сгущением.
Рис. 2- Расчетная сетка 51×51
Картину течения в каверне при Re=3200 наглядно отражает векторное поле скоростей и линии тока, представленные на рисунках 3-4.
Рис 3 - Векторное поле скоростей. (Re=3200)
Сетка 31×31.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.