Результаты, полученные без учёта радиационного теплообмена.
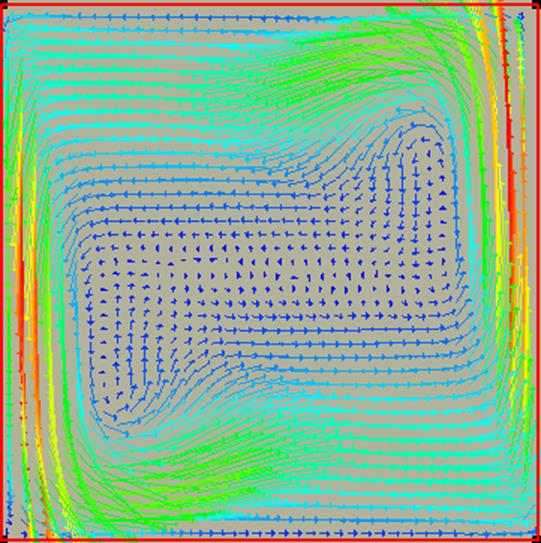
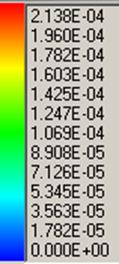
Рис.3 Поле скоростей (без радиации).
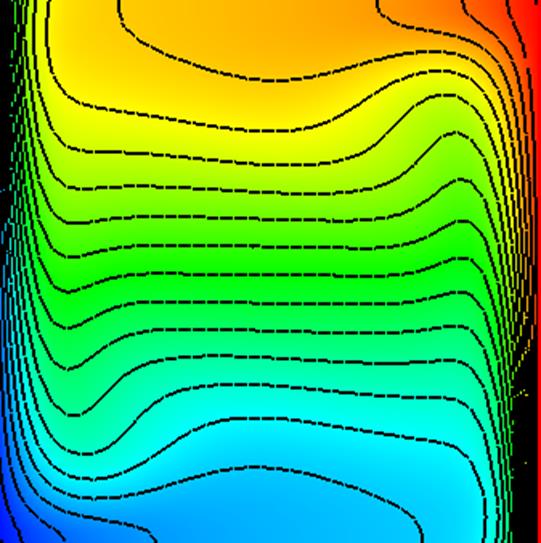
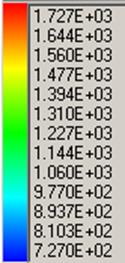
Рис.4 Изолинии температуры (без радиации).
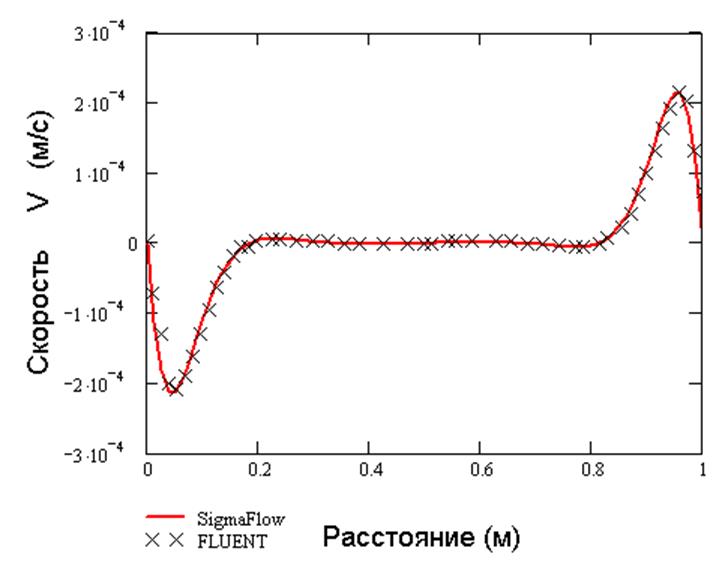
График Y компоненты скорости в сечении у=0.5 м (без радиации).
Из представленного графика видно хорошее совпадение расчета полученного при помощи σFlow с решением, полученным на FLUENT.
Результаты, полученные с учётом радиационного теплообмена.
В данном случае при расчете использовалась модель P-1 радиационного теплообмена.
Было произведено два варианта расчета с разным коэффициентом поглощения среды 0.2 и 5. Результаты расчета представлены
На рисунках 6-9.
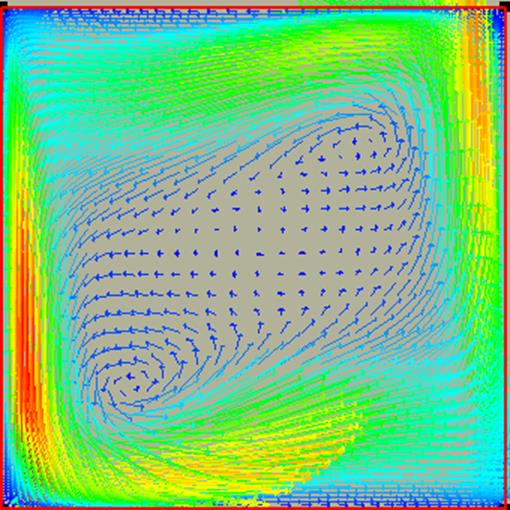

Рис.6 Поле скоростей (коэффициент поглощения 0.2).
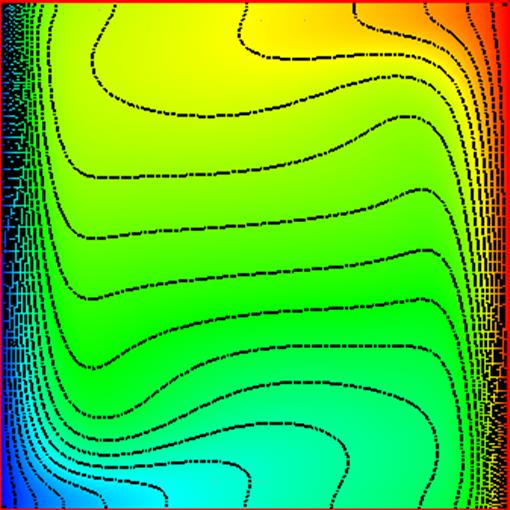

Рис.7 Изолинии температуры (коэффициент поглощения 0.2).
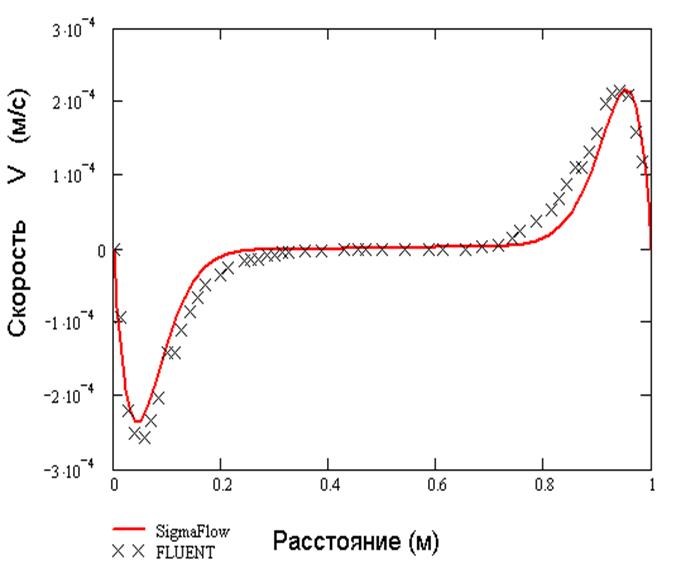
График V компоненты скорости в сечении у=0.5 м (коэффициент поглощения 0.2).
Из графика видно хорошее совпадение с радиационной моделью Р-1 заложенной в пакете FLUENT.
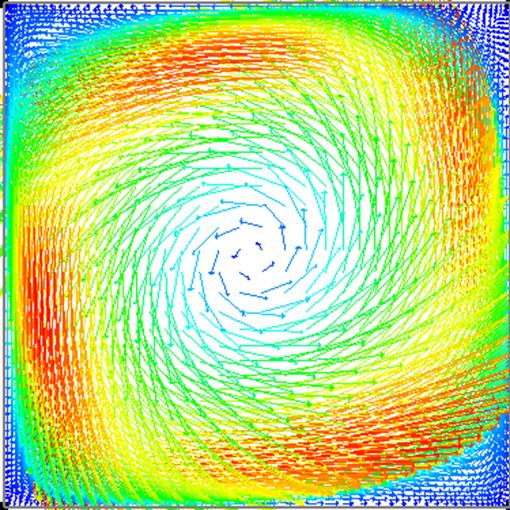

Рис.8 Поле скоростей (коэффициент поглощения 5).
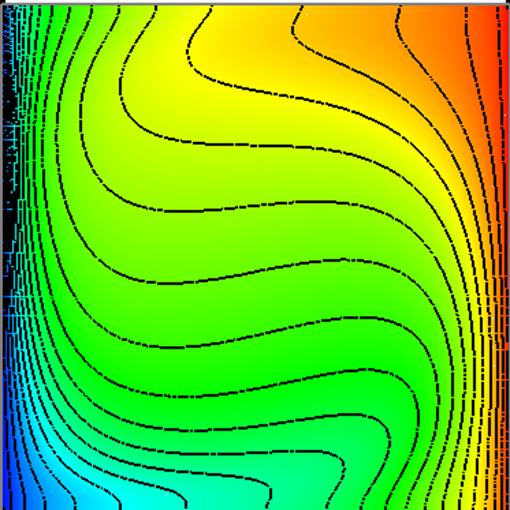

Рис.9 Изолинии температуры (коэффициент поглощения 5).
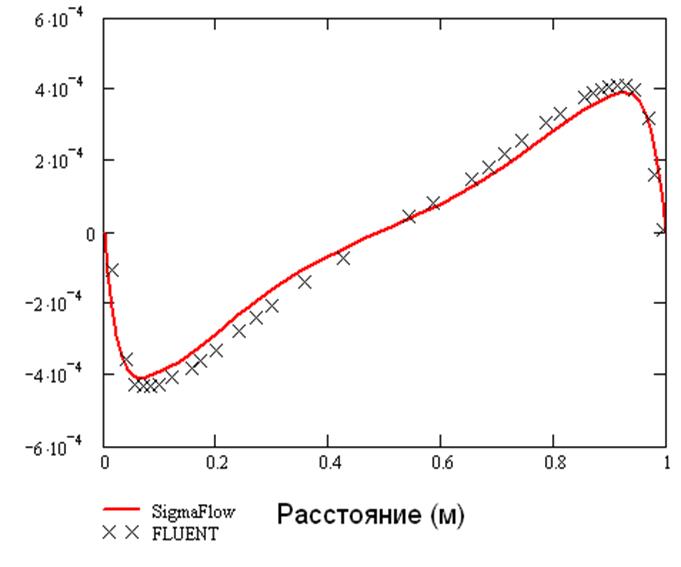
График V компоненты скорости в сечении у=0.5 м
(коэффициент поглощения 5).
6.8. Турбулентная свободная конвекция в вытянутой каверне
Геометрия задачи представлена на рисунке 1. Размеры каверны: W=0.076 м, H=2.18 м, D=0.52 м.
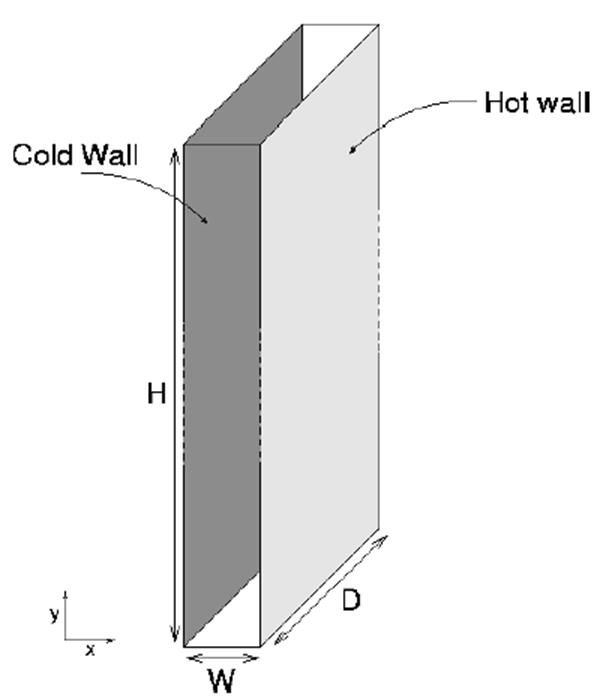
Рисунок 1. Геометрия каверны.
Каверна заполнена
воздухом, расчеты проводились при двух числах Релея![]() и
и
![]() .
.
Граничные условия: верхняя и нижняя
стенки адиабатические, температура боковых стенок при числе Релея ![]() равна 15˚С и 34.6˚С, температура
боковых стенок при числе Релея
равна 15˚С и 34.6˚С, температура
боковых стенок при числе Релея ![]() равна 15˚С и 54.9˚С.
равна 15˚С и 54.9˚С.
Сила тяжести направлена против оси Y.
Расчет производился на сетке 100×100×3.
Максимальное значение y+ равно 22 при ![]() и 26 при
и 26 при ![]() .
.
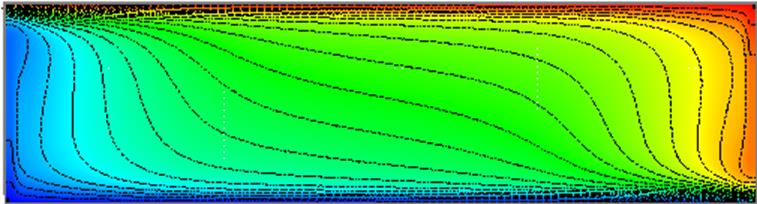
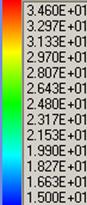
Изолинии температуры, ![]() . (Масштаб 0.25×H, 2×W)
. (Масштаб 0.25×H, 2×W)
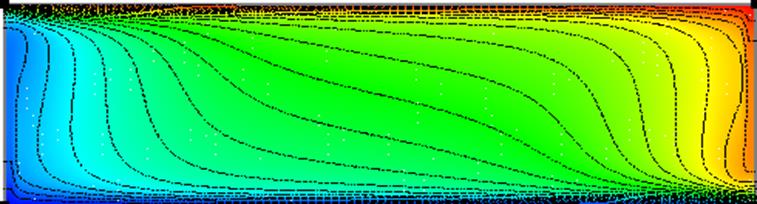
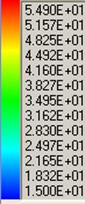
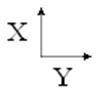
Изолинии температуры, ![]() . (Масштаб 0.25×H, 2×W)
. (Масштаб 0.25×H, 2×W)

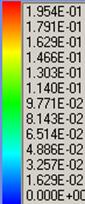

Линии тока, ![]() .(Масштаб 0.25×H, 2×W)
.(Масштаб 0.25×H, 2×W)

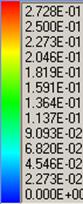

Линии тока, ![]() .(Масштаб 0.25×H, 2×W)
.(Масштаб 0.25×H, 2×W)
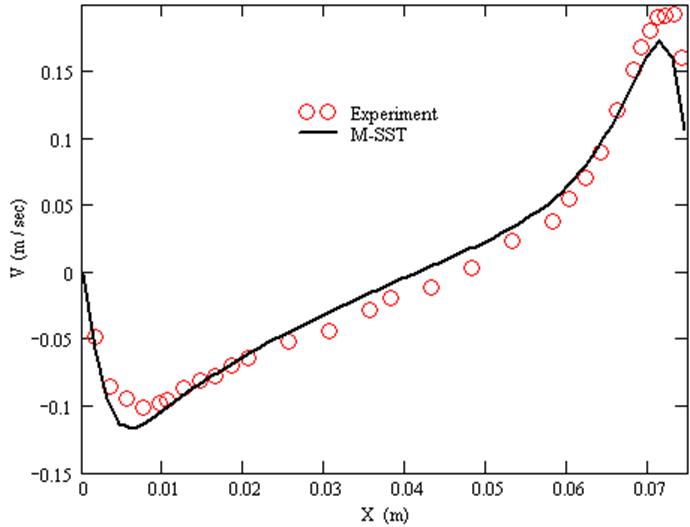
График V компоненты скорости при Y/H=0.1.
![]()
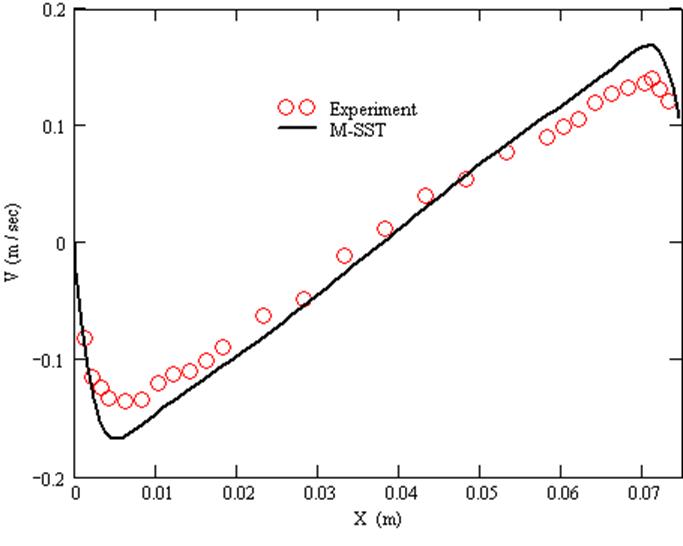
График V компоненты скорости при Y/H=0.5.
![]()
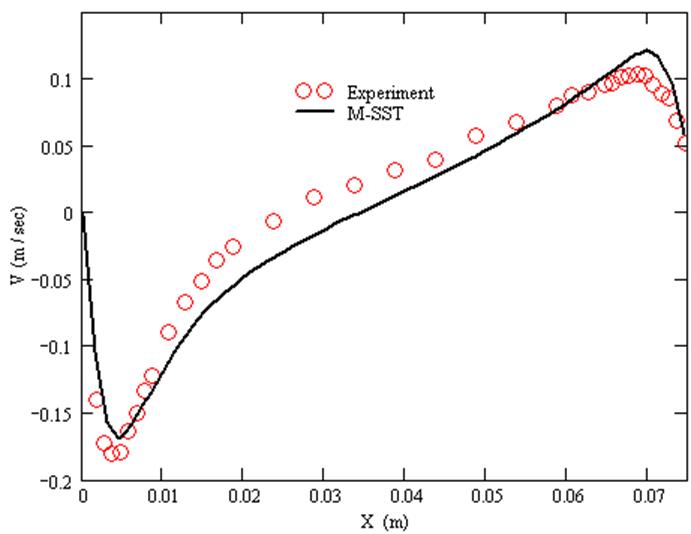
График V компоненты скорости при Y/H=0.9.
![]()
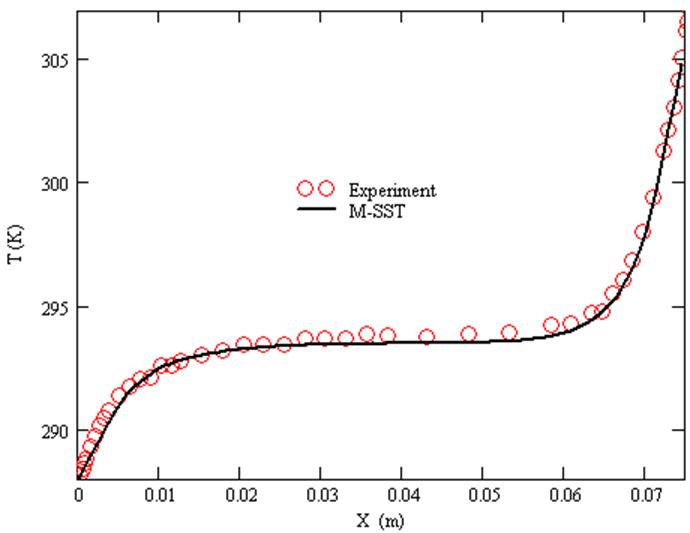
График температуры
при Y/H=0.1. ![]()
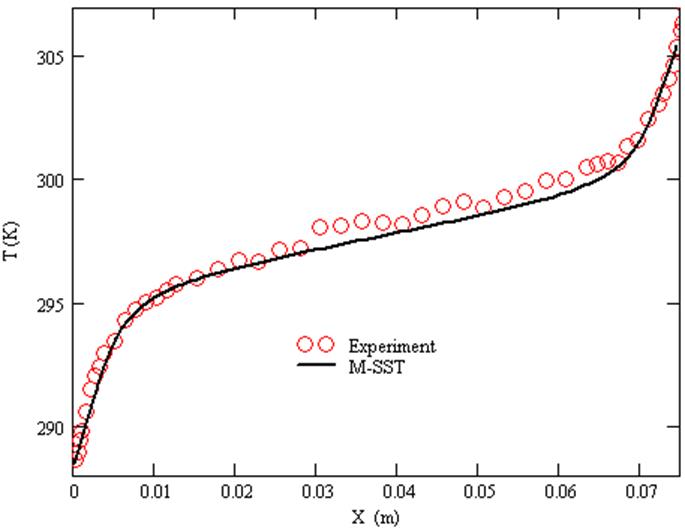
График температуры
при Y/H=0.5. ![]()
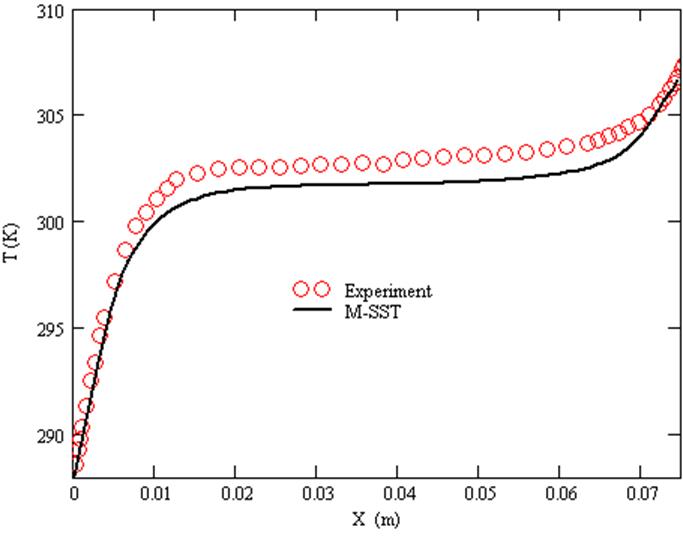
График температуры
при Y/H=0.9. ![]()
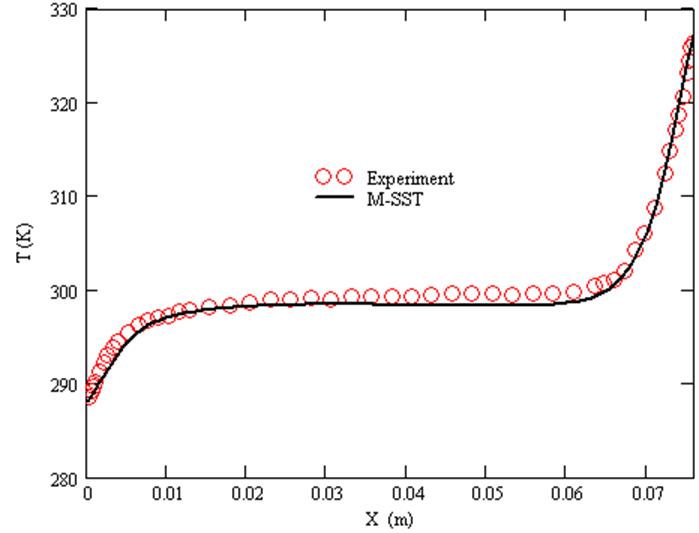
График температуры
при Y/H=0.1. ![]()
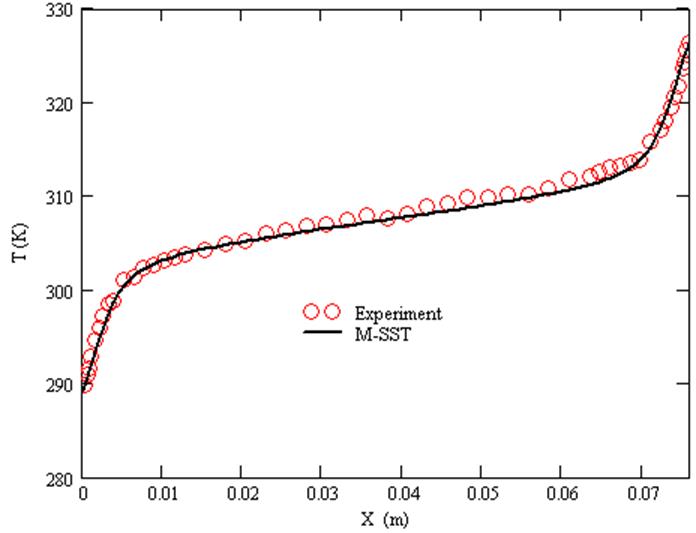
График температуры
при Y/H=0.5. ![]()
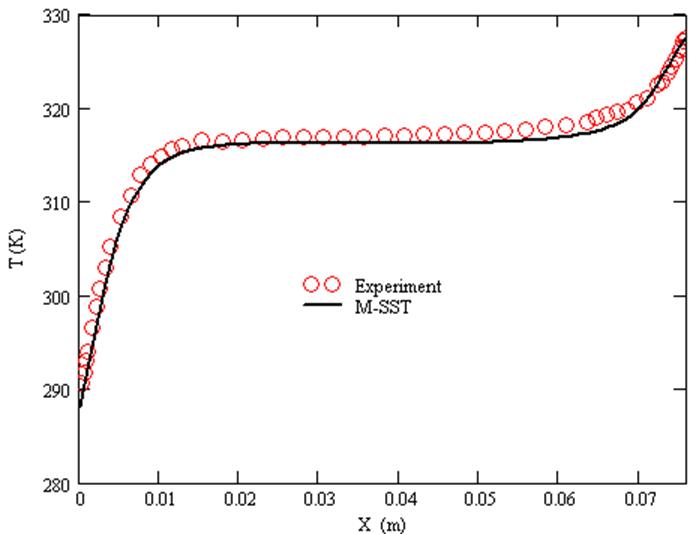
График температуры
при Y/H=0.9. ![]()
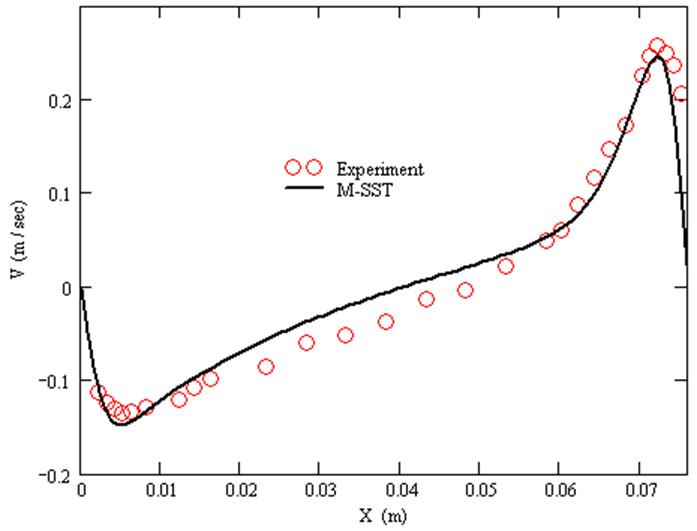
График V компоненты скорости при Y/H=0.1.
![]()
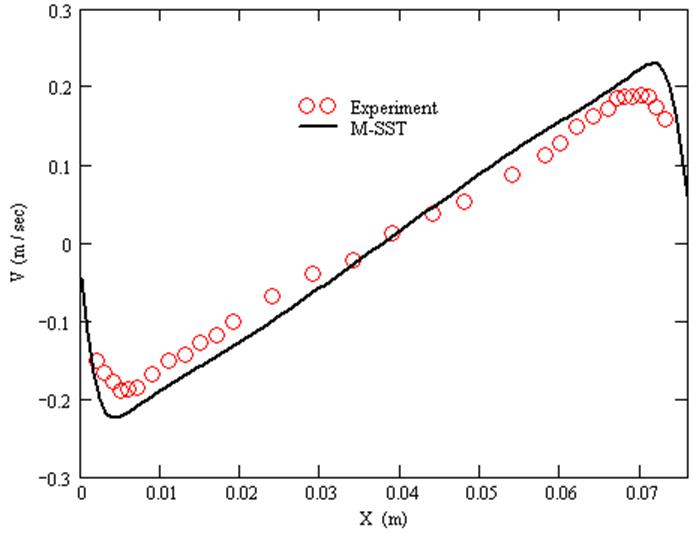
График V компоненты скорости при Y/H=0.5.
![]()
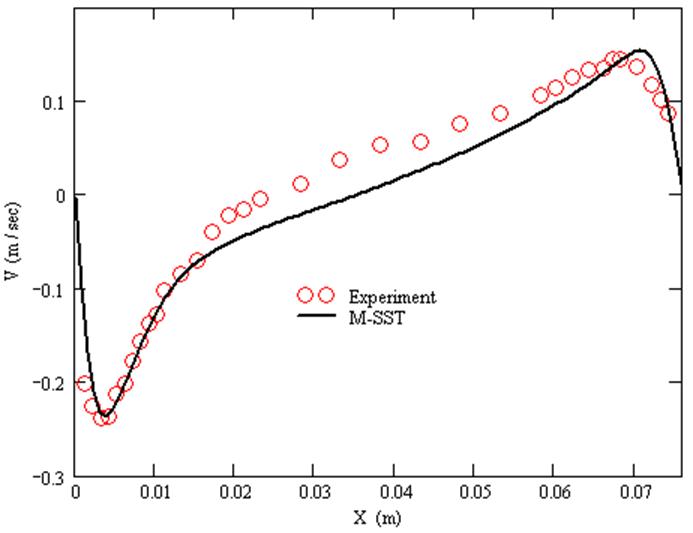
График V компоненты скорости при Y/H=0.9.
![]()
6.9. Турбулентный теплообмен в расширяющемся канале
Введение
С помощью пакета SigmaFlow было проведено моделирование процесса турбулентного теплообмена в расширяющейся трубе. Цель данной работы тестирование различных моделей турбулентности и сравнение полученных результатов с экспериментальными данными Baughn et al. [1]
Описание задачи
Канал представляет собой круглую трубу длиной 41 м (рис 1). Радиус входного сечения 0,665 м, радиус выходного сечения 1,665 м. Степень расширения 0,4. Длина узкого участка трубы 1 м, длина широкого участка 40 м.
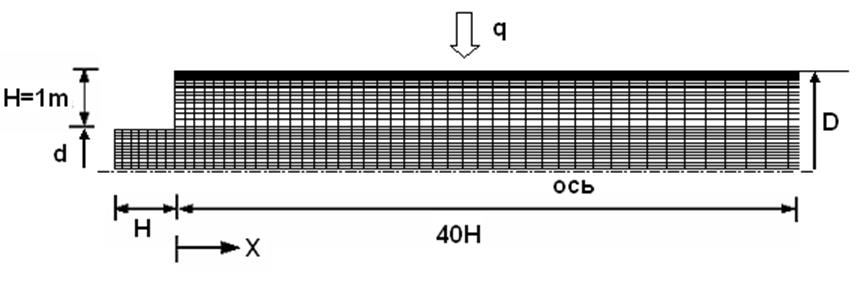
Рис1. Геометрия задачи.
Физические параметры
Теплофизические свойства среды представлены в таблице.
|
Молекулярная вязкость |
0,0001 Па×сек |
|
Коэффициент теплопроводности |
0,0001 Вт/(м×К) |
|
Теплоёмкость |
0,7 Дж/(кг×К) |
|
Плотность |
1,0 кг/м3 |
|
Число Прантдля |
0,7 |
|
Число Рейнольдса |
40680 (40750) |
|
Массовый расход |
10,64 кг/с |
|
Среднемассовая скорость |
7,659 м/с |
Число Рейнольдса определялось по диаметру широкого участка:
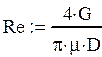
Граничные условия
Стенки узкой части канала считались адиабатическими, на стенках широкой части канала задавался тепловой поток 0,3 Вт/м2. Температура среды на входе в канал 273 К. На входе в канал задавался ударный профиль с уровнем турбулентности 1 % и масштабом турбулентности 0,16 м.
Сетка
Расчеты производились на трех сетках:
Grid 1: осесимметричный сектор 131´31´3 со сгущением к центральной оси и стенкам, y+ составлял в области рециркуляции 20¸200, вблизи выходного сечения ~60. Скорость счета - 0.095 сек/итерация.
Grid 2: трехмерная грубая сетка 82´25´25, y+ составлял в области рециркуляции 150¸850, вблизи выходного сечения ~150. Скорость счета - 1-0.6 сек/итерация.
Grid 3: укороченный вариант сетки 1 с длинной 20 м, осесимметричный сектор 71´31´3, y+ составлял в области рециркуляции 20¸200. Скорость счета - 0.05 сек/итерация.
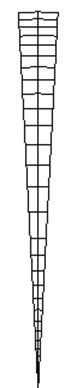

Рис. 2. Сетка 1.

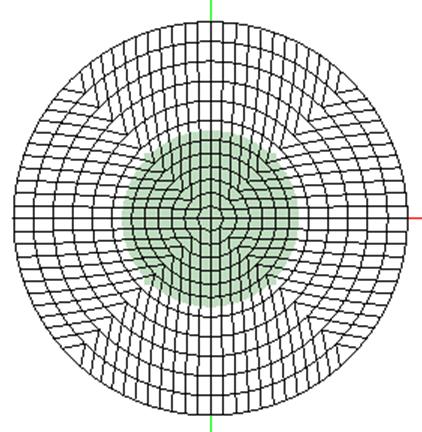 Рис. 3. Сетка 2.
Рис. 3. Сетка 2.
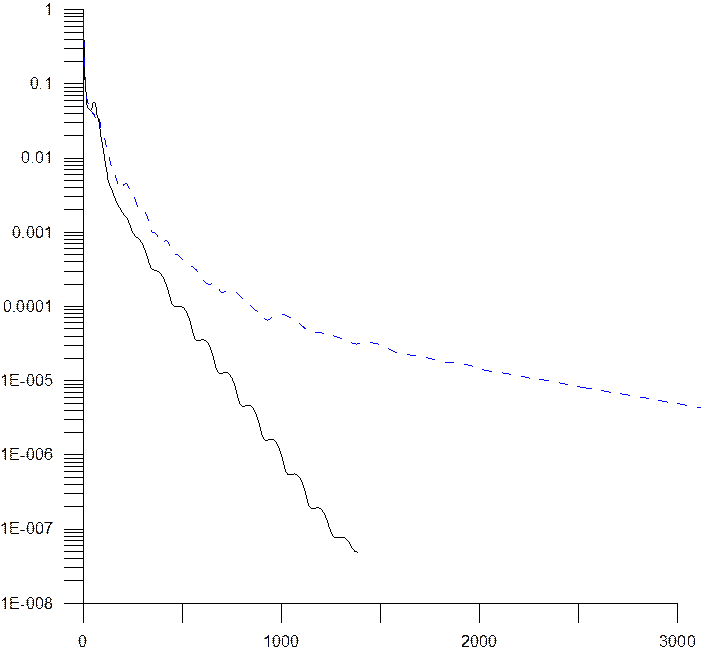
Рис. 4. Графики сходимости: пунктирная линия – сетка 1, сплошная линия – сетка 2.
Результаты
На рисунках 9-10 представлены распределения гидродинамических характеристик потока. В области за уступом формируется рециркуляционное течение. Протяжённость этой области в зависимости от параметров расчета колебалась от 8 до 11 м от уступа, что соответствует большинству экспериментальных данных. Количественной характеристикой, которая вычислялась в результате расчета, было локальное число Нуссельта на стенке. Число Нуссельта вычислялось при помощи температуры ядра потока
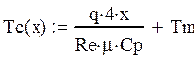
и коэффициента теплоотдачи на стенке:
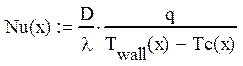
На графиках 5 и 6 представлено отношение локального числа Нуссельта на стенке Nu(x) к интегральному числу Нуссельта NuDB, посчитанному по критериальному соотношению для турбулентного режима течения в круглой трубе:
![]() .
.
Из графиков видно (рис. 5-6), что при удалении от уступа локальное число Нуссельта асимптотически стремится к интегральному. Максимум числа Нуссельта приблизительно совпадает с положением точки присоединения и удален от уступа на 8-10 м.
Расчеты производились при помощи трех моделей турбулентности: стандартная k-e модель, Chen k-e модель, модель M-SST. При проведении расчетов для уравнений переноса турбулентных характеристик использовалась TVD схем второго порядка точности, для уравнения переноса импульса – схема QUICK. Влияние порядка аппроксимации на результаты моделирования не исследовалось.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.