Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 11

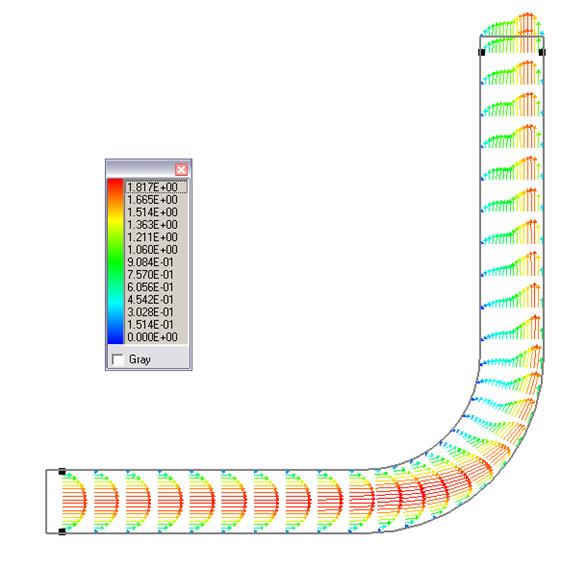
Рис. 3.Течение по центру канала

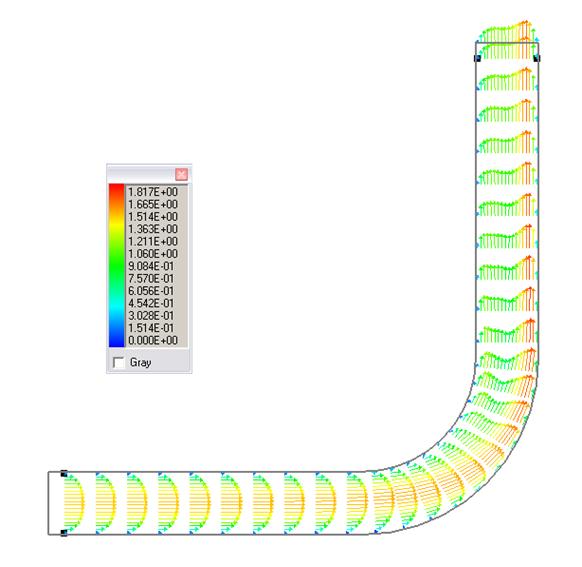
Рис. 4. Течение в плоскости Y=0.25 м

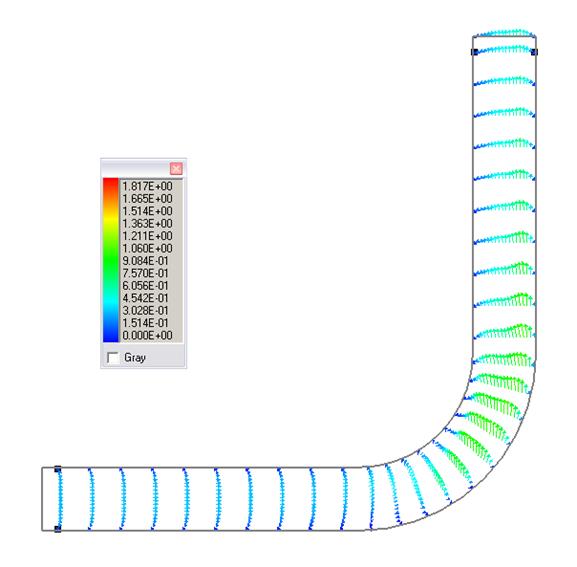
Рис. 5. Течение в плоскости Y=0.46

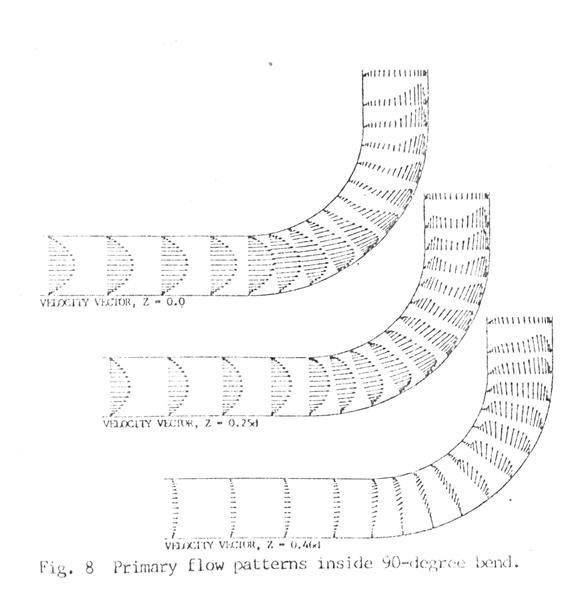
Рис. 6. Течение в гибе (Chen)

Рис. 7. Течение в поперечном сечении непосредственно перед гибом (угол 0 градусов)

Рис. 8. Течение в гибе (30 градусов)

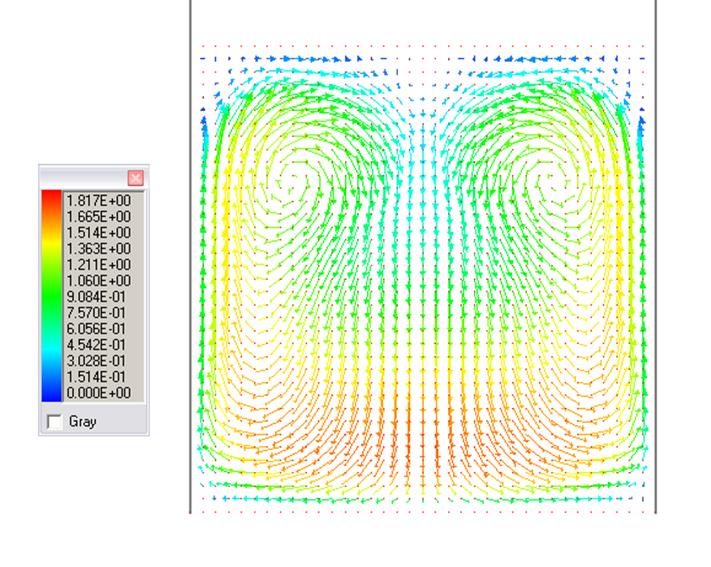
Рис. 9. Течение в гибе (60 градусов)

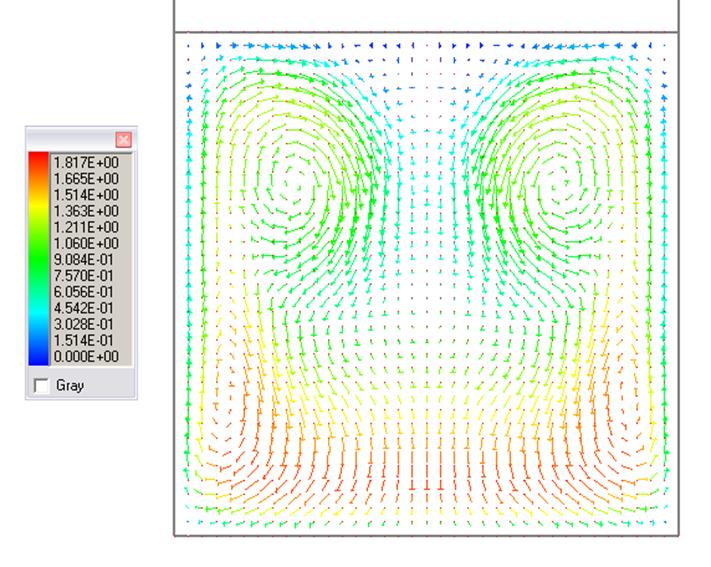
Рис. 10. Течение за гибом (90 градусов)

Количественное сравнение проводилось по профилям скорости вдоль радиуса, точнее, линии пересечения плоскости симметрии задачи с одним из перпендикулярных ей сечений. Сечение задается углом , имеющим смысл, указанный на Рис. 1. На Рис. 11 – 14 приведены профили скорости в сечениях , ,  и .

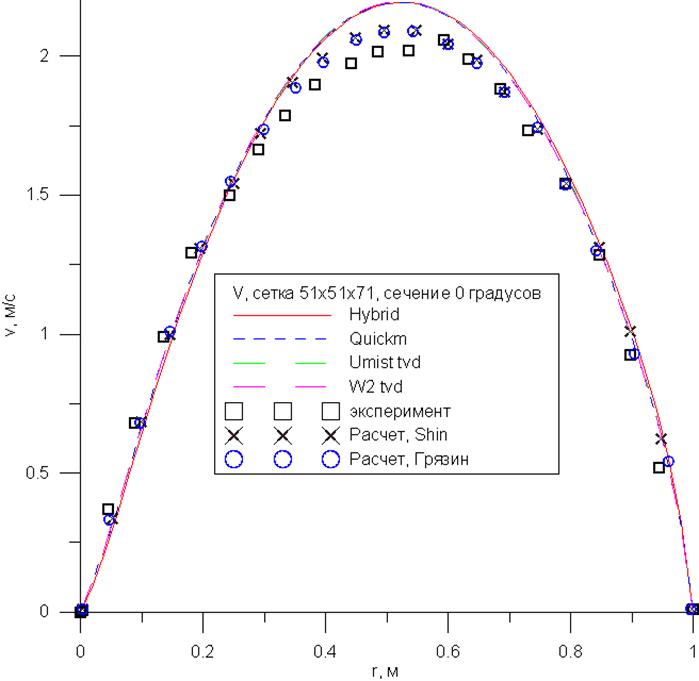
Рис 11. – Распределение продольной скорости по радиусу, .

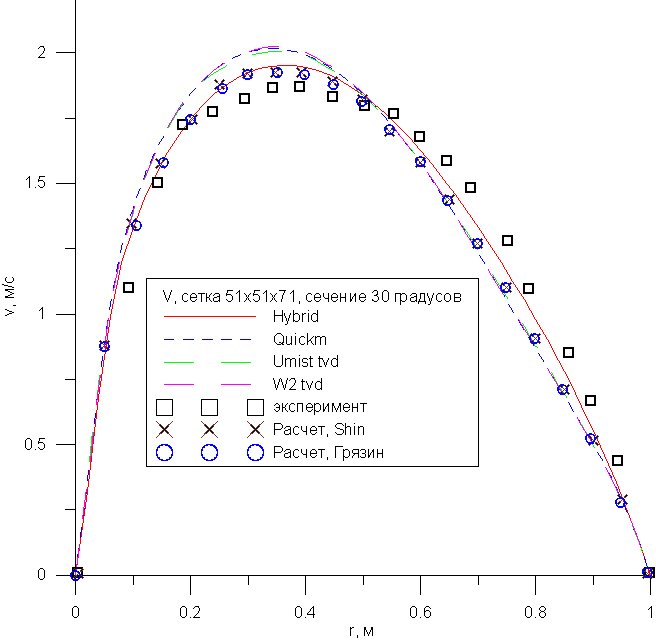
Рис 12. – Распределение продольной скорости по радиусу, .

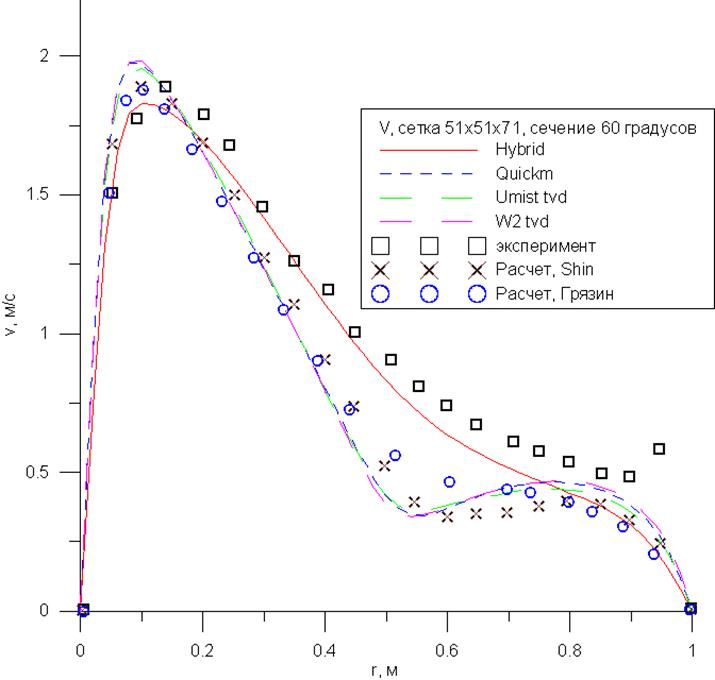
Рис 13. – Распределение продольной скорости по радиусу, .

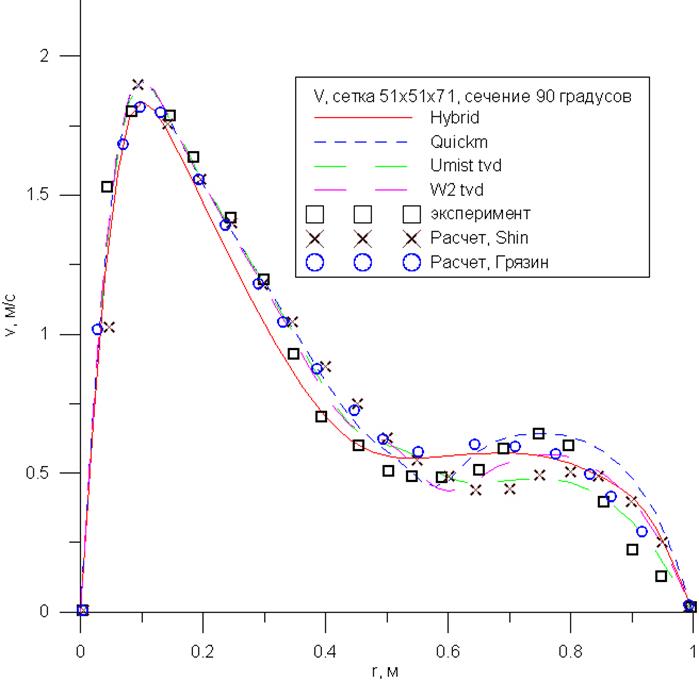
Рис. 14 – Распределение продольной скорости по радиусу, .

Литература

1. Chen, Y. S. Viscous flow computations using a second-order upwind difference scheme.

2. Грязин, Ю. А. Применение противопотоковых схем для численного моделирования задач гидродинамики на основе метода искусственной сжимаемости, дис. к. ф.-м. н. Новосибирск – 1996.

6.4. Ламинарное обтекание цилиндра

Введение.

В качестве примера использования пакета SigmaFlow в моделировании нестационарных задач, была решена задача о ламинарном обтекании круглого цилиндра.

Постановка задачи.

Цилиндр диаметром D=3м, нагретый до температуры 873К обтекается потоком холодной жидкости при температуре 273К.

Расстояние от цилиндра до стенок примерно 4D.

Теплофизические свойства жидкости представлены в таблице.

Плотность	1                     кг/м3
Динамическая вязкость	0.1                  Па*сек
Коэффициент теплопроводности	0.00001487    Вт/мК
Число Прандтля	0.7
Теплоемкость	1000               Дж/мК

Граничные условия.

Для вырождения задачи в двумерную, на торцах расчетной области задавались условия симметрии.

Сетка.

Расчетная сетка содержала 148×58×3 узла и была сгущена к цилиндру.

Рис.1 Расчетная сетка.

Результаты.

Стационарное обтекание цилиндра.

Расчеты проводились при различных числах Рейнольдса, результаты представлены на рисунках 2-13.

Исследования показали, что при  числах Рейнольдса меньших 5 наблюдалось ползущее течение, при котором не происходит отрыва погранслоя от поверхности цилиндра. Картина такого течения при Re=0.16 представлена на рисунках 2-4.

Рис.2 Векторное поле скоростей. Re=0.16

Рис.3 Линии тока. Re=0.16.

(верхняя половина взята из альбома Ван Дайка)

Рис.4 Изолинии температуры. Re=0.16.

При увеличении числа Рейнольдса до 6 происходит отрыв погранслоя с образованием двух симметричных вихрей. Это продемонстрировано на рисунках 5-7.

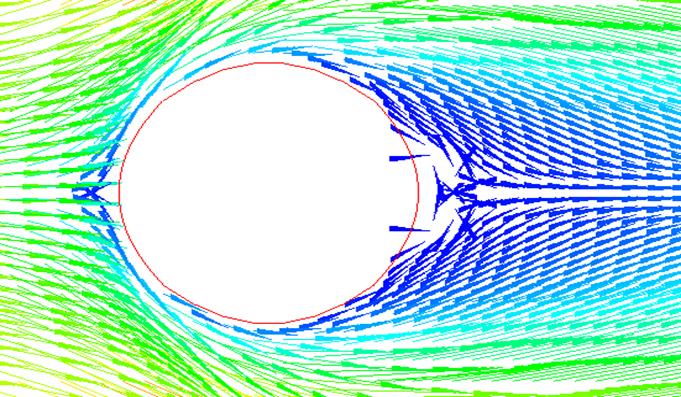
Рис.5 Векторное поле скоростей. Re=9.6

Рис.6 Линии тока. Re=9.6.

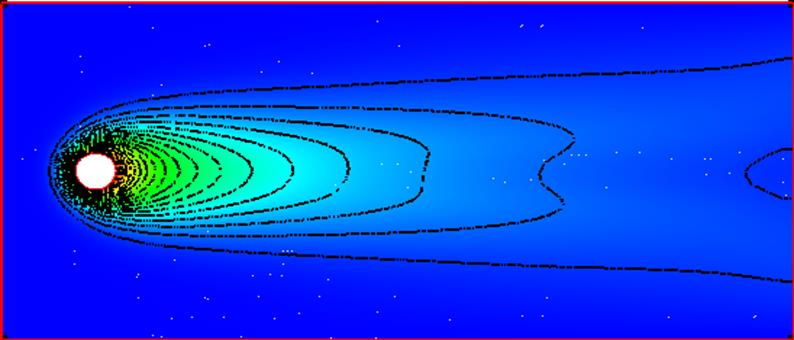
Рис.7 Изолинии температуры. Re=9.6.

Размеры вихревой области за цилиндром увеличиваются пропорционально числу Рейнольдса.

Рис.8 Векторное поле скоростей. Re=26

Рис.9 Линии тока. Re=26.

(верхняя половина взята из альбома Ван Дайка)

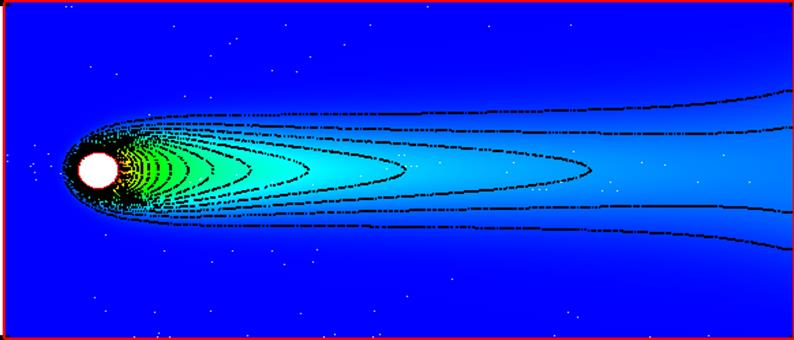
Рис.10 Изолинии температуры. Re=26.

Рис.11 Линии тока. Re=41.

(нижняя половина взята из альбома Ван Дайка)

Рис.12 Векторное поле скоростей. Re=50.

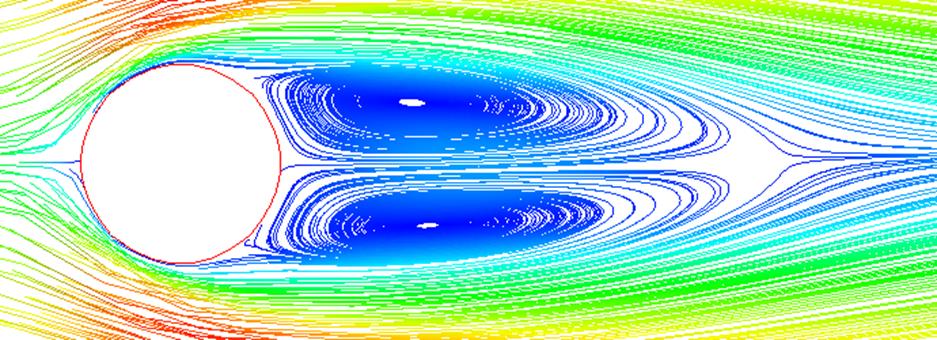
Рис.12 Линии тока. Re=50.

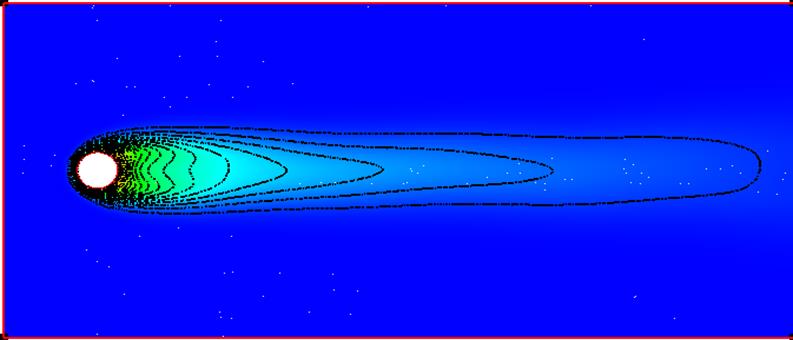
Рис.13 Изолинии температуры. Re=50.

Картина при Re=50 примерно соответствует верхнему пределу существования установившегося течения. Хотя вихри за цилиндром выглядят вполне симметричными, но след далеко вниз по потоку уже начал совершать синусоидальные колебания. Это особенно проявляется на изолиниях температуры. 

Нестационарное обтекание цилиндра.

При нестационарном обтекании рассматривался процесс роста рециркуляционной зоны за цилиндром при числе Re = 40. Результат представлен на рисунке 14 в виде зависимости от времени безразмерного размера вихревой области за цилиндром. Как видно расчет хорошо согласуется с экспериментом.

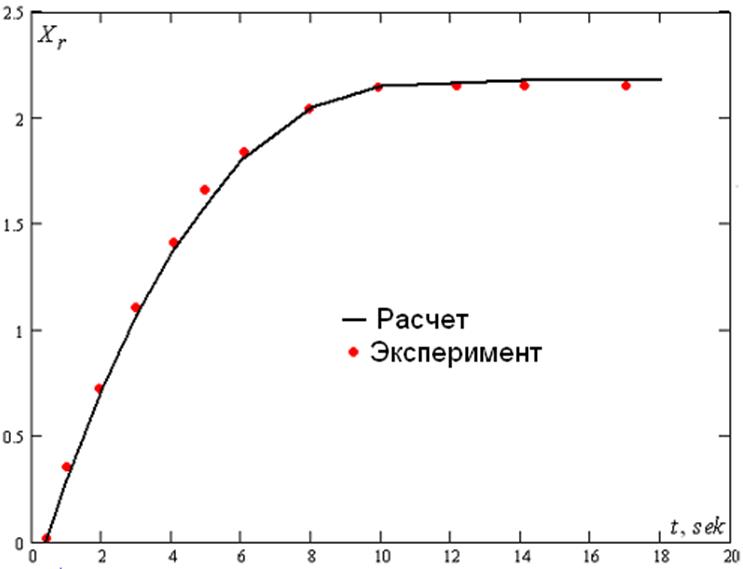
Рис.14. Длина рециркуляционной области за цилиндром при

Re=40.

При увеличении числа Рейнольдса свыше 45 течение становится нестационарным. Происходит периодический срыв вихрей, которые образуют за цилиндром вихревую дорожку Кармана. Картину такого течения  можно наглядно представить при помощи анимации поля температур (рис15).

Рис 15. Изолинии температуры при числе Re=200.

Для количественной оценки точности нестационарных расчетов проводилось сравнение с экспериментом зависимости числа Струхаля от числа Рейнольдса. Результаты представлены в таблице 1.

Таблице 1.

Re	Sh         (σFlow)	Sh     (эксперимент)
50	0.123	0.122
100	0.165	0.167
200	0.19	0.1895

6.5. Ламинарное течение жидкости в тройнике.

1.Введение.

Было проведено исследование ламинарного течения жидкости в тройнике прямоугольного сечения при различных числах Рейнольдса. Полученные результаты были сопоставлены с экспериментальными данными и расчетами, приведенными в справочных данных пакета FLUENT.6. 

2. Постановка задачи.

Тройник представляет собой канал прямоугольного сечения, к которому под прямым углом подсоединен другой прямоугольный канал  как показано на рисунке 1. Характерные размеры тройника L = 3 м и W = 1 м. Высота канала в направлении оси Z равна 2.11 м.

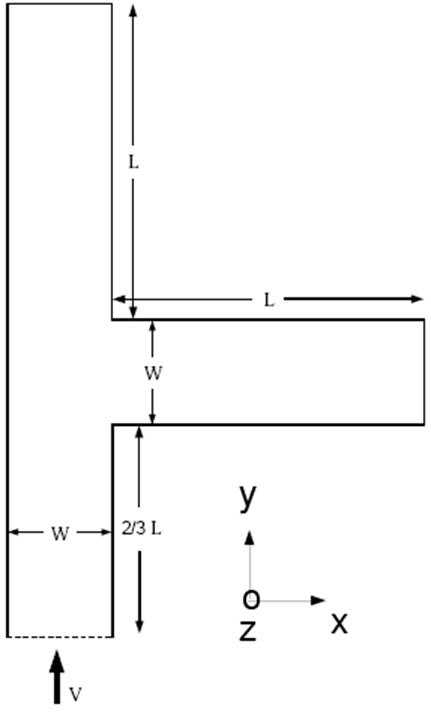
Рис.1 Геометрия задачи.

3. Физические свойства жидкости и граничные условия.

Расчеты проводились для чисел Рейнольдса равных .  Число Рейнольдса определялось по формуле:

,

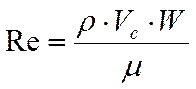где  – плотность потока,  – динамическая вязкость,  – скорость жидкости в центре канала на входе в тройник, – ширина входа. Плотность задавалась равной единице. На входе в тройник задавался параболический профиль скорости. Скорость в центре канала задавалась равной единице. Среднемассовая скорость при этом равнялась 0.667. Для соответствующих чисел Рейнольдса динамическая вязкость приведена в таблице 1.  На выходах давление задавалось равным нулю. Для проведения двухмерных расчетов на стенках тройника, параллельных плоскости Z, задавались условия скольжения. На остальных стенках задавалось условие прилипания.