Моделирование на разных сетках показало, что расчеты на 3D сетке (сетка 2) обладают лучшей сходимостью чем расчеты на 2D сетках (рис. 4). Это связано с итерационной реализацией условия скольжения на оси и боковых поверхностях для сеток 1 и 3. Сравнение локального числа Nu полученного на разных сетах с использованием модели Chen приведено на рис. 5. Из рисунка видно, что результаты, полученные на грубой сетке (сетка 2), значительно отличаются от эксперимента, предсказывая завышенные числа Nu и более короткую зону рециркуляции (рис. 8). Результаты, полученные на плоских сетках 1 и 3, очень хорошо описывают эксперимент и практически совпадают друг с другом. Это совпадение говорит об отсутствии влияния близости выходного сечения на результаты моделирования.
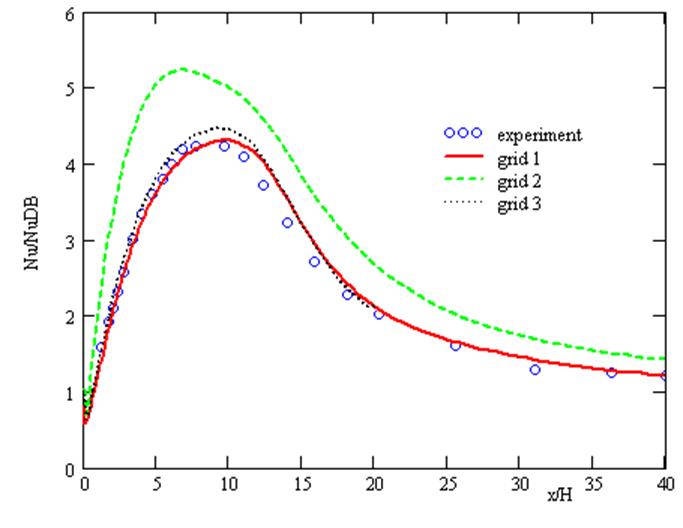
Рис. 5. Относительное число Нуссельта на стенке канала за расширением. Сравнение сеток.
На сетке 2 распределение числа Nu полученные по модели Chen и M-SST совпадают в ближней зоне (x<5H) и за точкой присоединения (x>15H), отличие проявляется в расположении максимума и его значения (рис. 6а). Удовлетворительное совпадение с экспериментом объясняется грубым разрешением сетки.
На рис. 6б представлено сравнение экспериментальных данных с расчетными значениями числа Nu, полученными на сетке 3 с использованием:
Chen Chen k-e модель и закон стенки с узловыми значениями,
Standart - стандартной k-e моделью,
Chen, walllaw 2 Chen k-e модель и закон стенки с интегральными значениями,
Chen, high Chen k-e модель с повышенным уровнем турбулентности на входе.
Подтверждается известный факт того, что стандартная k-e модель плохо описывает пристеночные течения и отрывом и присоединением потока. Для данной задачи существенным оказалось влияние степени турбулентности входящего потока, что видно из графика 6б. С увеличением степени турбулизации потока укорачивается зона рециркуляции, и максимум локального числа Nu смещается вверх по потоку. Интересно, что результаты стандартной k-e модели и результаты модели Chen с повышенной турбулентностью на входе совпадают как по теплоотдаче (рис. 6б), так и по трению (рис. 7б).
Различные реализации метода пристеночных функций показали отличные друг от друга результаты. Реализация закона стенки с узловыми значениями членов генерации и диссипации турбулентной энергии очень хорошо описывает эксперимент. Вариант закона стенки с членами генерации и диссипации турбулентной энергии, проинтегрированные с использованием логарифмического профиля, дает правильное расположение максимума теплоотдачи и точки прилипания, но с заниженными значения числа Nu.
а)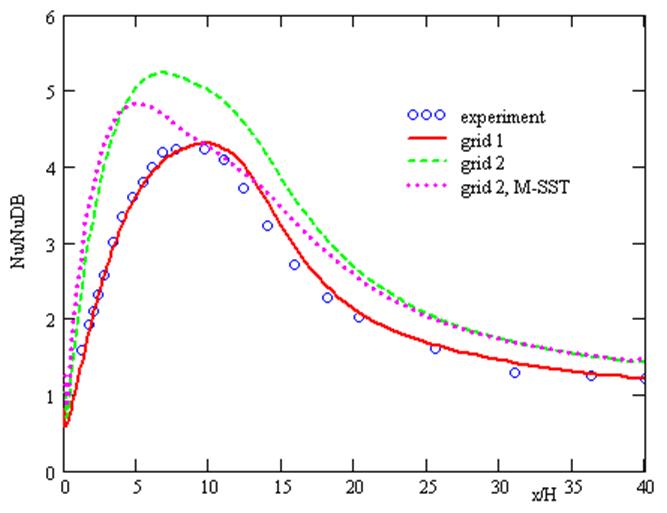
б)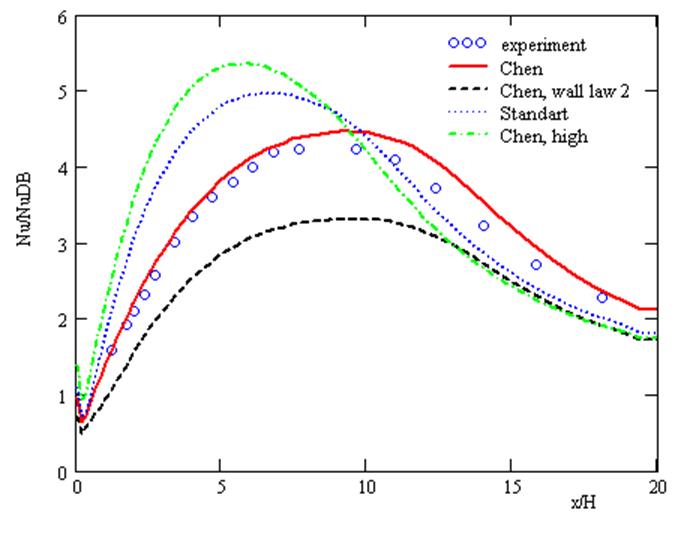
Рис. 6. Относительное число Нуссельта на стенке канала за расширением. Сравнение методик.
В качестве дополнительной иллюстративной информации приведены распределения коэффициента трения (рис. 7) и коэффициента давления (рис. 8) на стенке канала за расширением.
а)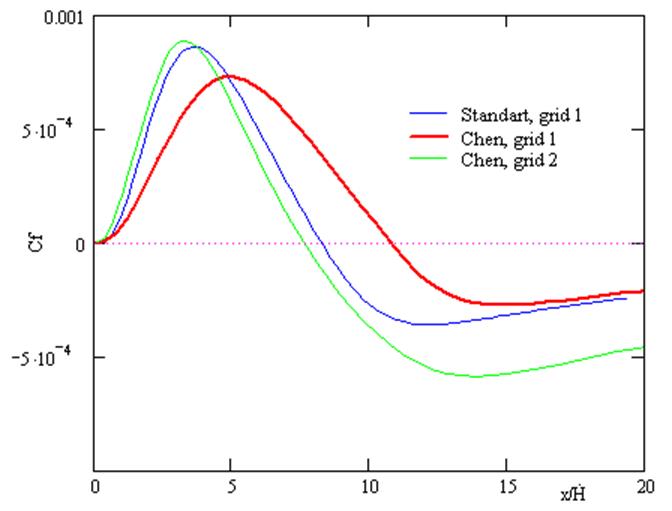
б)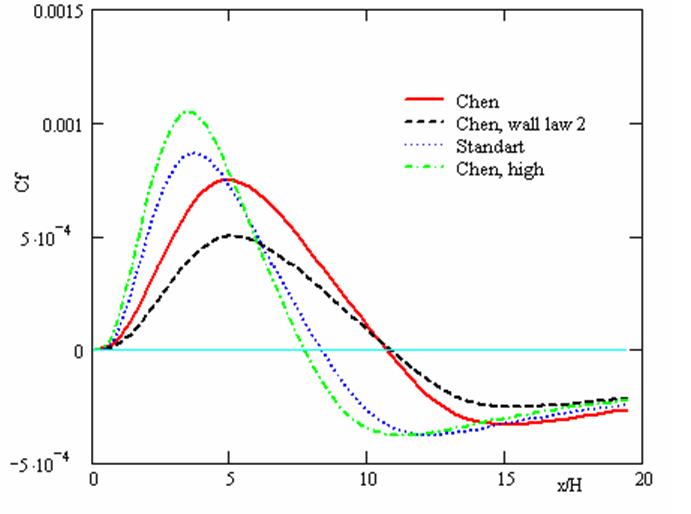
Рис. 7. Коэффициент трения: а) сравнение сеток, б) сравнение методик.
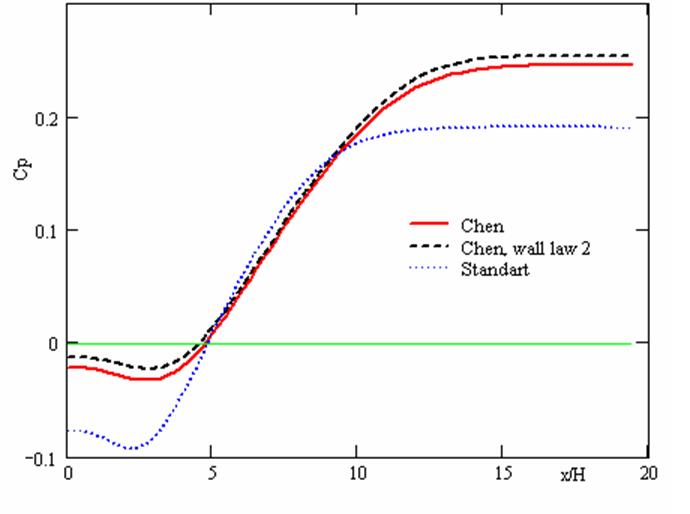
Рис. 8. Коэффициент давления. Сравнение моделей.


Рис. 9. Траектории частиц.
 а)
а)
 б)
б)
 в)
в)
 г)
г)
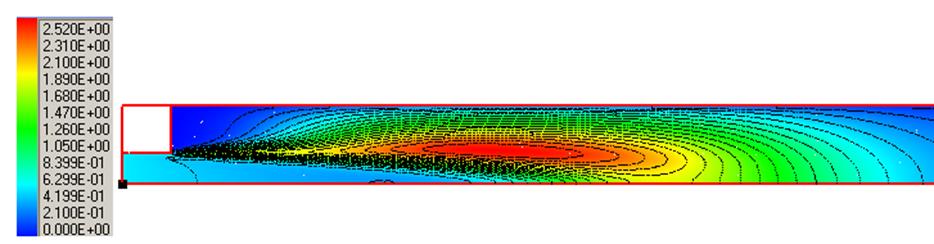
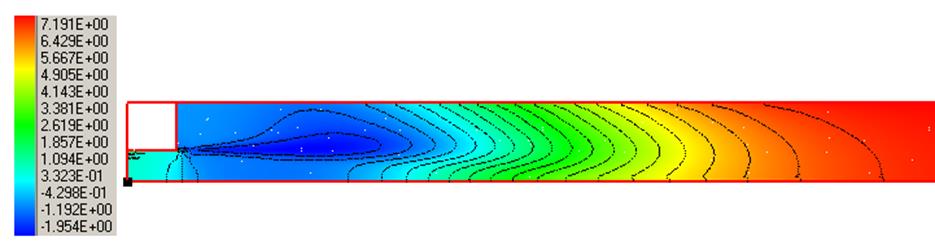
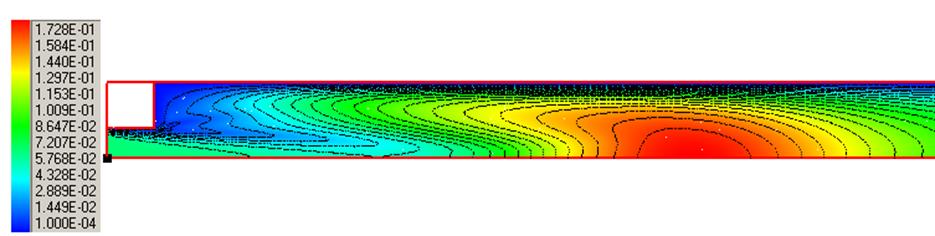
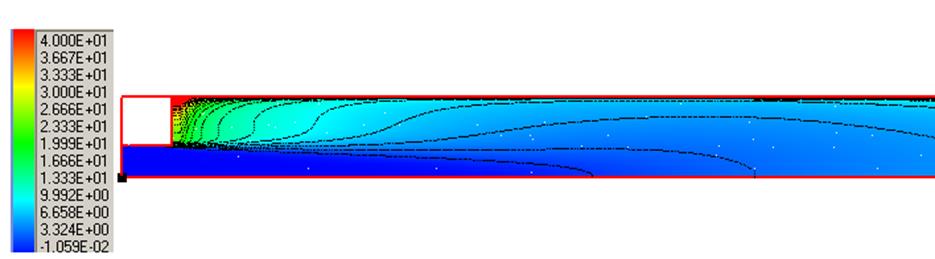
Рис. 10. Картина течения:
а) энергия турбулентных пульсаций, б) поле давления, в) турбулентная вязкость, г) поле температуры.
Список используемых источников
1. Лойцянский Л. Г. Механика жидкости и газа. М.: Наука, 1970. 840 c.
2. Андерсон, Дж. Таннехилл, Р. Плетчер Вычислительная гидромеханика и теплообмен. М.: Мир, 1990. Т. 1-2. 726 с.
3. Chen, Y.S., and Kim, S.W. 1987. Computation of turbulent flows using an extended k-e turbulence closure model, NASA CR-179204.
4. R. Siegel and J. R. Howell. Thermal Radiation Heat Transfer. Hemisphere Publishing Corporation, Washington D.C., 1992.
5. Magnussen, B.F., and Hjertager, B.W. 1981. ‘On the structure of turbulence and a generalised eddy dissipation concept for chemical reaction in turbulent flow’, 19th AIAA Aerospace Meeting, St. Louis, USA.
6. K.Gorner. Simulation turbulenter Stromungs- und Warmeubertragungsvorgange in Grosfeuerungsanlagen. Dissertation, Stuttgart. 1987.
7. Crow C.T., Sharma M.P., Stock D.E. The Particle-Source-In Cell (PSI-CELL) Model for gas droplet flows //Journal of Fluids Engineering. P. 325.
8. Бабий В.И., Куваев Ю.Ф. Горение угольной пыли и расчет пылеугольного факела. М.: Энергоатомиздат, 1986.-208 с.
9. Зельдович Я.Б., Садовников П.Я., Франк-Каменецкий Д.А. Окисление азота при горении. М.: Изд-во АН СССР, 1947. 317 с.
10.Fenimore C.P. Studies of fuel-nitrogen in rich flame gases // 17th Symp. (Intl.) Comb., The Combustion Institute, Pittsburgh, 1979, P.661.
11.de Soete, G. 1974, Overall reaction rates of NO and N2 formation from fuel nitrogen, 15th Symp. (Int.) on Comb., Pittsburgh, pp 1093-1102.
12.Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984. 152 с.
13.Булеев Н.И. Пространственная модель турбулентного обмена. М.: Наука, 1989. 343с.
14. Bradshow Себиси Т., Бредшоу П. Конвективный теплообмен. Физические основы и вычислительные методы: Пер. с англ.- М.: Мир, 1987.-592 с.
15. ISAEV, Белов И.А., Исаев С.А., Коробков В.А. Задачи и методы расчета отрывных течений несжимаемой жидкости. Л.: Судостроение, 1989. 256 с.
16. Chen, Y.S., and Kim, S.W. 1987. Computation of turbulent flows using an extended k-e turbulence closure model, NASA CR-179204.
17. Menter F.R. Zonal two equation k-w turbulence models for aerodynamic flows // AIAA Paper. 1993. № 93-2906. 21 p.
18. Esch T., Menter, F. R. Heat tranfer prediction based on two-equation turbulence models with advanced wall treatment, in Proc. Turbulence Heat an Mass Transfer, Eds. Hanjalic, Nagano, Tummers, Antalya, 2003.
19. B. Kader. Temperature and Concentration Profiles in Fully Turbulent Boundary Layers. Int. J. Heat Mass Transfer, 24(9):1541-1544, 1993.
20. C. Jayatilleke. The Influence of Prandtl Number and Surface Roughness on the Resistance of the Laminar Sublayer to Momentum and Heat Transfer. Prog. Heat Mass Transfer, 1:193-321, 1969.
21. B. E. Launder and D. B. Spalding. The Numerical Computation of Turbulent Flows. Computer Methods in Applied Mechanics and Engineering, 3:269-289, 1974.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.