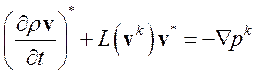Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 8

                                             (3.4.32)

2. Расчет поправки давления и определение давления

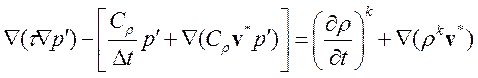                       (3.4.33)

В силу не строгости уравнения поправки давления, временной шаг Dt в квадратных скобках можно заменить на локальный параметр t:

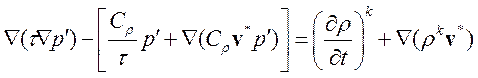.            (3.4.33а)

3. Коррекция скорости

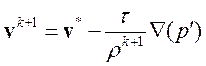                                          (3.4.34)

Значения на нулевой итерации выбираются равными значениям с предыдущего временного слоя:

                                     (3.4.35)

Для анализа уравнения поправки давления введем понятие «скорости звука»

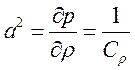                                                    (3.4.36)

и числа Маха

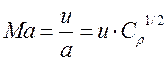.                                              (3.4.37)

Отношение диффузионного потока к конвективному составляет величину порядка

.

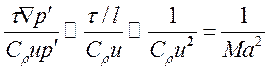При течениях с малым числом Маха, т.е. дозвуковых течениях, оператор Лапласа доминирует над конвективным членом в уравнении (3.4.33) и мы получаем классическое уравнение Пуассона для давления:

.

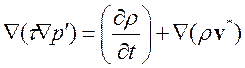С другой стороны, при течениях с большим числом Маха, т.е. сильно сжимаемых течениях, оператором Лапласа можно пренебречь и уравнение давления принимает гиперболический вид, отражающий волновую природу сжимаемых течений:

.

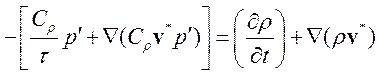Таким образом, выше описанный метод пригоден для моделирования течений с любым числом Маха.

Численная реализация уравнения для поправки давления

Рассмотрим решение уравнения для поправки давления:

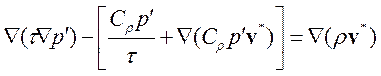                           (3.4.1.1)

Последовательно проинтегрируем по контрольному объему, в центре которого находится узел P , все части уравнения.

Интегрирование диффузионной части дает выражение:

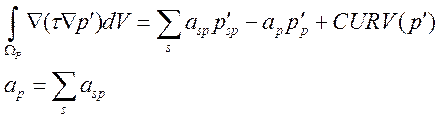,                 (3.4.1.2)

где слагаемое CURV объединяет члены, появляющиеся из-за криволинейности сетки. При построении разностного аналога диффузионного члена используются центрально-разностные схемы.

Для построения разностного аналога конвективного части необходимо использовать противопоточную аппроксимацию на гранях контрольного объема. При применение схем высокого порядка аппроксимации (выше первого) явно выделяются части, соответствующие схеме с односторонними разностями (коэффициенты b_sp) и слагаемые, повышающие порядок аппроксимации (COR), т.е. разность между схемой высокого порядка и направленными разностями первого порядка:

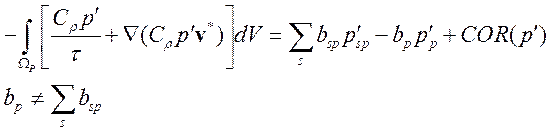             (3.4.1.3)

Результат интегрирования правой части представляется суммой массовых потоков через грани контрольного объема:

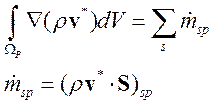                                        (3.4.1.4)

Использование направленной аппроксимации плотности при нахождении потоков массы через грань контрольного значительно улучшает сходимость решения. Для «правой» грани противопоточную аппроксимацию массового потока можно записать следующим образом:

           (3.4.1.5)

Скорость на грани вычисляется линейной интерполяцией соседних узловых величин:

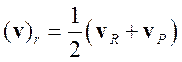.                                            (3.4.1.6)

В результате объединения разностных аналогов всех частей уравнения для поправки давления получаем систему уравнений:

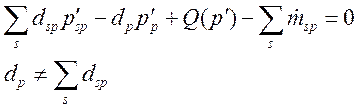                              (3.4.1.7)

Слагаемые, связанные с неортогональностью сетки и применением схем высокого порядка (Q), учитываются итерационно:

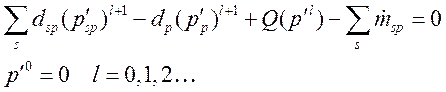.                (3.4.1.8)

Таким образом, для учета неортогональных слагаемых и построения схем высокого порядка аппроксимации, требуется введения дополнительного итерационного процесса. Часто для упрощения расчетов и уменьшения времени счета эти слагаемые опускают

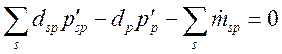.                                        (3.4.1.9)

Известно, что при расчетах на совмещенных сетках необходимо принимать специальные меры, для того чтобы не допустить осцилляций давления. Для этого в уравнение поправки давления необходимо добавить слагаемое, обеспечивающее монотонизацию поля давления [Peric]. Введение монотонизатора часто рассматривается как добавление поправки в любую грань контрольного объема, величина которой определяется разностью между градиентами давления, вычисленными на одинарном и двойном шаге (интерполяция Rhie-Chow). Так например поток через «правую» грань будет вычисляться как:

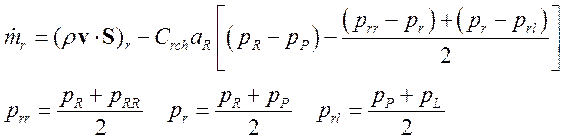           (3.4.1.10)

или

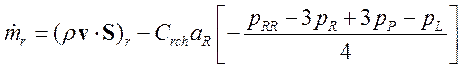                         (3.4.1.10а)

где C_rch– коэффициент, обычно равный 0,1, a_R – правый коэффициент матричного оператора диффузионной части уравнения для поправки давления.

Следует обратить внимание, что при вычислении массовых потоков через грань контрольного объема являющуюся граничной для избежания экстраполяции давления за границу расчетной области монотонизирующая поправка не вводится.

Граничные условия

Граничное условие с заданным полным давлением не рассматривается.

В отсутствии массовых сил на всех границах (вход, выход, стенки, симметрия) для поправки давления и давления используется граничные условия типа Неймана:

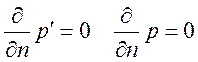.                                          (3.4.2.1)

В случае заданного давления (p_set) на выходной границе используются условия типа Дирихле:

.                                               (3.4.2.2)

Моделирование течений с объемными силами, например свободно-конвективных течений, на совмещенной сетке осложняется необходимостью задания адекватных граничных условий (ГУ) для давления. Использование граничного условия 2-го рода (3.1) может приводить к отсутствию баланса между объемной силой и градиентом давления вблизи границ, в результате чего поле течения значительно искажается. Граничное условие

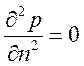                                                           (3.4.2.3)

или замена центральных разностей на направленные от границы разности при аппроксимации градиента давления в уравнении импульса (в примере левая грань граничная)

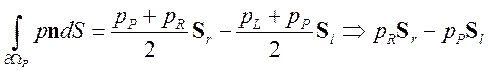           (3.4.2.4)

позволяют сохранить баланс сил.

Алгоритм решения

Решение с помощью данного численного метода состоит из последовательности шагов (итераций). Сходимость считается достигнутой, если будет выполнен следующий критери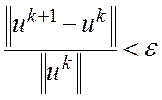й:

       и 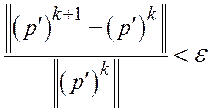                                                         (3.4.3.1)

где    

, - значения скорости на текущей и предыдущей  итерации при решении уравнений количества движения;

p¢ - поправка давления на итерации;

e- заданная точность расчета.

Общая процедура расчета представлена следующей последовательностью операций:

1. Задание начального поля давления p.