Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 3

Для описания турбулентных характеристик течения в пакете “sFlow” реализован следующий набор  моделей турбулентности:

Стандартная k-e модель (standard)

Уравнения стандартной высоко-рейнольдсовой k-e модели:

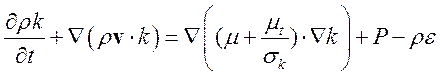                            (1)

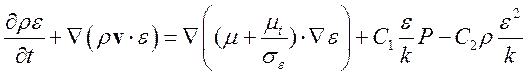                          (2)

где P - скорость генерации турбулентности:

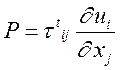,                                                     (3)

турбулентная вязкость:

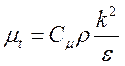.                                                    (4)

Тензор Рейнольдсовых напряжений принимает форму:

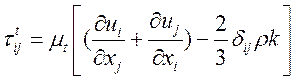.                                      (5)

Константы замыкания стандартной модели [Standard]:

C_m=0,09, s_k=1,0, s_e=1,3, С₁=1,44, C₂=1,92.

Chen k-e модель

Уравнения для модификации k-e модели Chen, которые определяют кинетическую энергию турбулентности и скорость ее диссипации для k-e модели, имеют вид [Chen]:

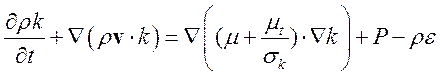                            (6)

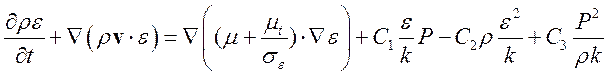                         (7)

Эмпирические константы C_m=0,09, s_k=0,8, s_e=1,15, С₁=1,15, C₂=1,9, C₃=0,25 взяты из работы [Chen].

M-SST модель турбулентности

Модель Ментера записывается путем суперпозиции моделей k-e и k-w, основанной на том, что модели типа k-e лучше описывают свойства свободных сдвиговых течений, в модели -w имеют преимущество при моделировании пристеночных течений. Плавный переход от k-w модели в пристеночной области к k-e модели вдали от твердых стенок обеспечивается введением весовой эмпирической функцией F₁ .

Вторая важная деталь модели состоит в изменении стандартной связи между k, w и турбулентной вязкостью. Модификация этой связи состоит во введении перехода к формуле Бредшоу в пристеночной области. Согласно предположению Бредшоу напряжение сдвига в пограничном слое пропорционально энергии турбулентных пульсаций.

Уравнения M-SST модели [M-SST]:

Транспортные уравнения для k и w

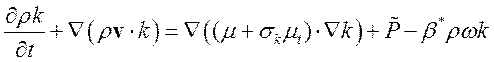                     (8)

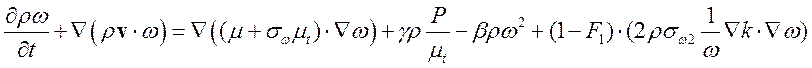          (9)

В члене генерации турбулентной энергии введен ограничитель:

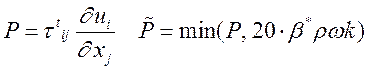                                       (10)

Весовая функция и ее аргумент

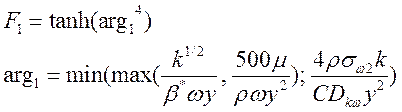,                                 (11)

где положительная часть перекрестных диффузионных членов в уравнении переноса w

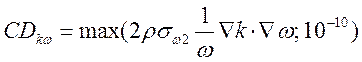.                                       (12)

Выражения для вихревой вязкости с учетом гипотезы Бредшоу:

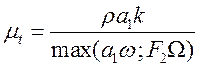,                                                    (13)

где величину завихренности можно определить соотношением

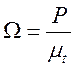.                                                           (14)

Функция переключения F₂ определяется подобно F₁ :

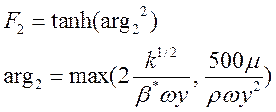.                                                             (15)

Константы в уравнениях переноса записываются путем суперпозиции констант для модели k-w модели (Wilcox) и констант стандартной k-e модели:

константы:

                                     (16)

Набор констант для пристеночного слоя SST модели:

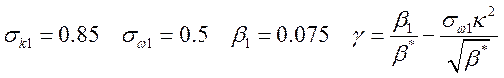.                            (17)

Набор констант для свободных сдвиговых слоев:

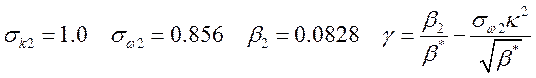.                        (18)

Другие константы, использующиеся в модели:

                                                (19)

Детали реализации

Линеаризация и неявный учет членов диссипации в правой части:

                                                       (20)

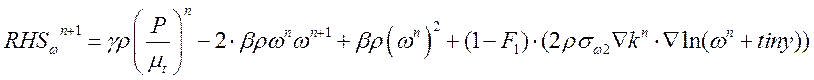          (21)

Метод пристеночных функций

Вблизи стенок турбулентный поток имеет сложную структуру со значительными градиентами. Во внутренней области, занимающей порядка 20% толщины пограничного слоя, генерируется около 80% всей энергии турбулентности. Для моделирования пристеночных течений часто применяется метод пристеночных функций, который позволяет экономить вычислительные ресурсы и учитывать влияния различных факторов (шероховатости стенки, градиента давления вблизи стенки, вдув-отсос с поверхности тела) за счет введения эмпирической информации. Метод пристеночных функций, связывающий параметры течения с расстоянием до стенки, представляет собой аналитическое решение упрощенных решений турбулентного течения.

В основе упрощения лежат следующие предположения [ISAEV]:

1) локальное равновесие энергии турбулентных пульсаций (локальная скорость производства турбулентности уравновешивается скоростью вязкой диссипации);

2) постоянство касательного напряжения вдоль слоя;

3) пренебрежимо малый градиент давления вдоль потока;

4) локальная изотропность диссипирующих вихрей;

5) универсальность профиля скорости (слабая зависимость от числа Рейнольдса).

Следует отметить, что этот метод является в основном эмпирическим. Метод пристеночных функций, основанный на обобщении экспериментальных данных для развитых турбулентных течений, достаточно хорошо описывает пристеночные течения при значительных турбулентных числах Рейнольдса с пренебрежимо малой областью вязкого слоя. В случае не выполнения гипотез, лежащих в основе пристеночных функций, требуется модификация соотношений метода или использование низкорейнольдсовых диссипативных моделей.

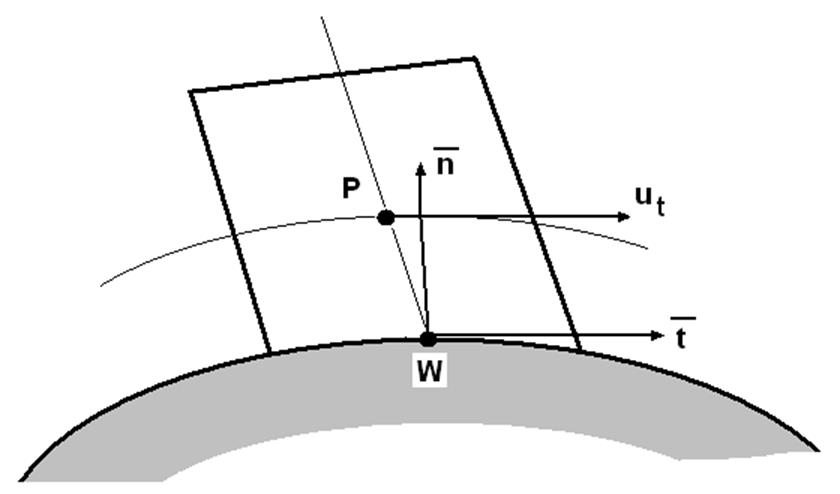
Динамический пограничный слой

На рис. 2 показан профиль продольной составляющей осредненной скорости в турбулентном пограничном слое. Использованы безразмерные величины для скорости

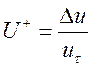                                                          (1)

и для расстояния до стенки

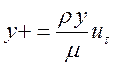,                                                      (2)

где введена динамическая скорость

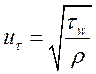.                                                        (3)

Пристеночная область разбивается на две зоны:

1) вязкий подслой (0<y+<5), в котором вязкие напряжения доминируют над рейнольдсовыми, а профиль скорости линейный:

                                                           (4)

2) турбулентный логарифмический слой (30<y+<400), где рейнольдсовы напряжения намного превышают вязкие и имеет место логарифмическая зависимость скорости от расстояния до стенки:

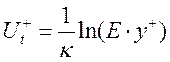.                                              (5)

Для сшивки профилей скорости в буферном слое (5<y+<300) применяется подход, предложенный Kader [Kader]:

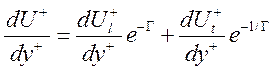                                          (6)

с фактором плавного сопряжения:

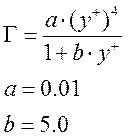.                                                    (7)