Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 2

·  в системе с подвижными границами;

дисперсная фаза -

·  PSIC (Лагранжев  подход),

·  метод взаимопроникающих континуумов (Эйлеров подход);

горение -

·  метод глобальной реакции (топливо+ окислитель=продукты) с моделью обрыва вихря и кинетическим механизмом;

объемные силы –

·  воздействие электромагнитного и гравитационного поля;

1. Основные уравнения

1.1. Уравнения ламинарного режима течения.

Согласно современным представлениям достаточно реалистическая картина многомерных течений жидкости или газа может быть получена на основе решения уравнений динамики вязкого газа. Для ламинарного режима течения такие уравнения могут быть записаны в форме уравнений Навье-Стокса.

Уравнение сохранения массы или уравнение неразрывности имеет вид:

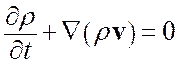.                                                                                        (1.1.1)

Уравнения сохранения количества движения:

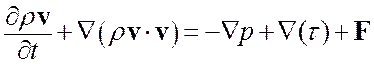                                                                                (1.1.2)

где -тензор вязких напряжений, - вектор объемных сил.

Составляющие тензора вязких напряжений  определяются как:            

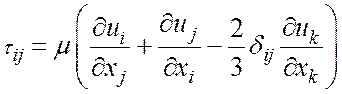                                                               (1.1.3)

где - динамическая (молекулярная) вязкость, - компоненты вектора скорости.

1.2. Уравнения турбулентного режима течения.

Считается, что при помощи уравнения Навье-Стокса можно описать как ламинарное так и турбулентное течение [1], практически же реальные достижения в расчетах  турбулентных потоков связаны с использованием полуэмпирических моделей турбулентности использующих подход Рейнольдса.

Применив операцию осреднения по времени к уравнениям (1.1.1) и (1.1.2) получим уравнения движения в форме Рейнольдса (RANS).

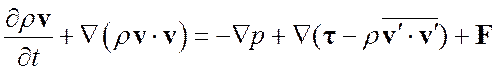                                                  (1.2.1)

где - усредненное по времени поле скоростей, - тензор рейнольдсовых напряжений, - символ Кронекера.

Для определения компонент тензора рейнольдсовых напряжений  используем гипотезу Буссинеска

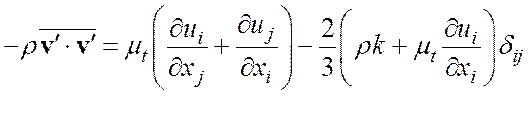                                              (1.2.2)

где - турбулентная вязкость, - кинетическая энергия турбулентных пульсаций.

Система уравнении (1.2.1)-(1.2.2) является не замкнутой поэтому для ее замыкания применяются различные полуэмпирические модели турбулентности которые описаны в разделе 2.

1.3. Уравнение энергии

В  пакете “sFlow” уравнение сохранения энергии рассматривается в следующем виде:

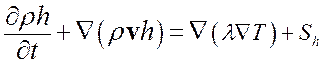                                                                           (1.3.1)

где  - коэффициент теплопроводности,  – источниковый член, отвечающий за изменение количества тепла в процессе химического реагирования, излучения, или каких-либо других процессах.

Энтальпия газа определяется по правилу смеси

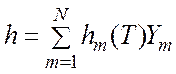                                                                                      (1.3.2)

где энтальпия компонент h_m(T) вычисляется как

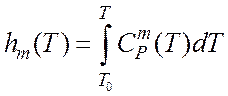.                                                                              (1.3.3)

 Удельная теплоемкость компонент задается в виде полинома 4-ой степени от температуры

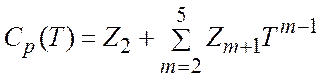.                                                                (1.3.4)

Температура смеси Т в каждой точке рассчитывается из уравнения (1.3.2) по вычисленному из уравнения (1.3.1)  значению энтальпии  и найденному из уравнения (1.4.1) составу смеси .

1.4. Уравнение переноса компонент среды

Уравнение переноса концентрации компонент:

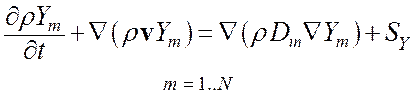                                                    (1.4.1)

где - массовая доля m-той компоненты,- коэффициент диффузии компонента m, – источниковый член, отвечающий за изменение массы в процессах химического реагирования  или в каких-либо других процессах. 

1.5. Термодинамические свойства среды

Уравнения состояния

1. Несжимаемая жидкость

                                                                                                              (1.5.1)

где -константа.

2. Модель термического расширения

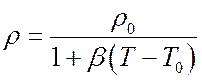                                                                                             (1.5.2)

где - коэффициент термического расширения, -опорная температура, -опорная плотность.

3. Модель идеального газа

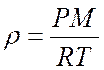                                                                                                           (1.5.3)

где P статическое давление, M - молярная масса газа, R - универсальная газовая постоянная, T - температура газа,

Свойства смеси

В программе “sFlow” свойства смеси определяются через массовые доли ее компонент .

Теплопроводность смеси

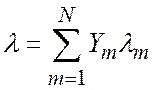                                                                                                   (1.5.4)

Плотность смеси

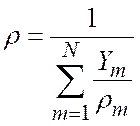                                                                                                      (1.5.5)

Удельная теплоемкость смеси

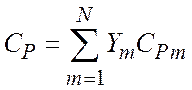                                                                                              (1.5.6)

Энтальпия смеси

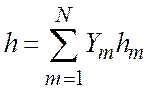                                                                                                    (1.5.7)

Динамическая вязкость смеси

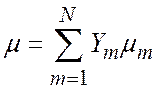                                                                                                   (1.5.8)

Молярная масса смеси

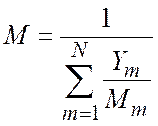                                                                                                   (1.5.9)

2.2. Моделирование турбулентных течений

Считается, что при помощи уравнения Навье-Стокса можно описать как ламинарное так и турбулентное течение [1], практически же реальные достижения в расчетах  турбулентных потоков связаны с использованием полуэмпирических моделей турбулентности использующих подход Рейнольдса. Обоснованием необходимости применения такого подхода может служить приведенная в ряде работ оценка, согласно которой отношение характерных размеров энергосодержащих (крупных) вихрей и мелкомасштабных вихрей, определяющих «турбулентный фон», имеет порядок Re^3/4. Естественно, что, ориентируясь на возможности современных ЭВМ, решить поставленные задачи в практически важном диапазоне Re ³ 10³ в настоящее время маловероятно.