Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 4

Это сопряжение хорошо описывает реальный профиль внутренней части пограничного слоя. На рис. 1 приведено сравнение безразмерной скорости и ее производной, полученной сшивкой по Kader, с эмпирической формулой [Bradshow]:

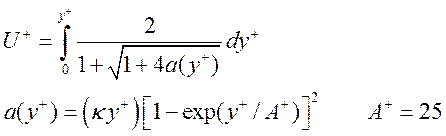.                (8)

Отличие проявляется в распределении производной скорости в области буферного слоя.

Изменение продольной составляющей скорости в пределах от стенки до ближайшего расчетного узла находится

,                                               (9)

где t_w – единичный касательный к поверхности стенки вектор.

Используя определение динамической скорости (3) и соотношение для безразмерной скорости (1) касательные напряжения на стенке можно записать следующим образом:

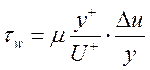.                                                 (10)

Это формула используется для расчета диффузионного потока импульса через грань контрольного объема, совпадающего со стенкой. Производная продольной скорости по нормали к стенке находится по своему конечно-разностному аналогу с учетом с учетом нелинейной зависимости профиля скорости от расстояния до стенки:

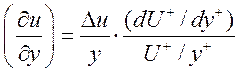.                                    (11)

Предположение о постоянстве касательных напряжений вдоль слоя дает выражение для турбулентной вязкости:

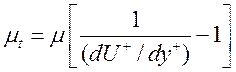.                                    (12)

а)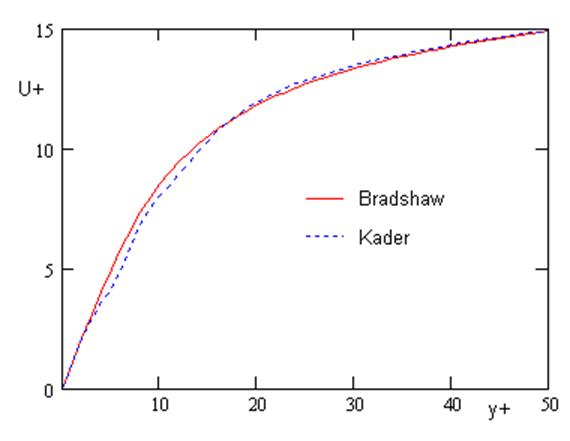

б)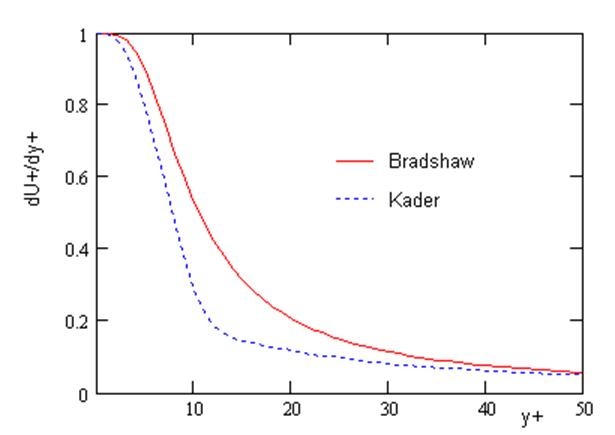

Рис. 1. Профиль безразмерной скорости и ее производной.

Тепловой пограничный слой

Соотношения, приведенные для динамического пограничного слоя, обобщаются на тепловой подслой. Вводя определение безразмерной температуры через перепад удельной энтальпии между стенкой и ближайшим узлом

 с учетом кривизны сетки                          (13)

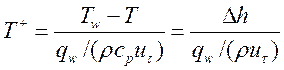                                         (14)

тепловой поток через стенку можно записать в виде:

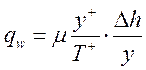.                                                 (15)

Выполняя требование о том, чтобы тепловой поток не зависел от расстояния до стенки, получаем выражение для эффективной теплопроводности:

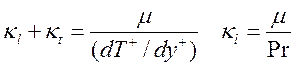.                                      (16)

Градиент энтальпии связан с перепадом энтальпии соотношением:

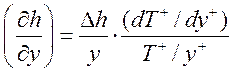.                                     (17)

Плавное сопряжение вязкого подслоя

                                                       (18)

и логарифмического турбулентного

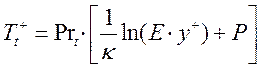                                  (19)

реализуется методом Kader:

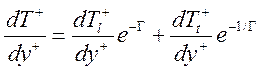.                                 (20)

Фактор сопряжения для теплового подслоя зависит от числа Прандтля среды:

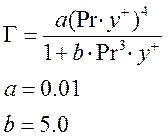.                                              (21)

В литературе встречается несколько вариантов определения коэффициента P (19), являющегося функцией отношений молекулярного и турбулентного чисел Прандтля.

Приведем некоторые:

[Launder]

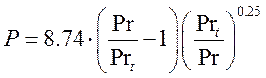                                           (22а)

[Jayatilleke]

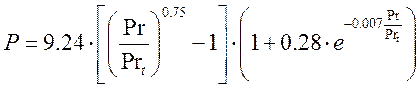.                              (22б)

Выражения (22) дают значения практически одинаковые значения.

Турбулентные характеристики

k-e модель:

При решении уравнения на k правая часть модифицируется, чтобы учесть в касательные напряжения (10). При этом поток диффузии энергии k через грань, совпадающую со стенкой приравнивается к нулю:

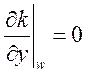.                                               (23)

Разностное уравнение для e в свою очередь модифицируется так, чтобы в пристеночном узле получалось значение соответствующее локальному равновесию:

                                                  (24)

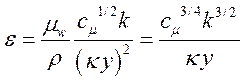                                    (25)

Вариант 1 (узловое значение)

В члене генерации турбулентных пульсаций производная  находится из условия локального равновесия:

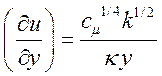.                                               (26)

В результате имеем:

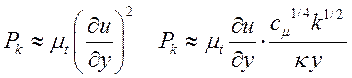                               (27)

Выражение для диссипации турбулентных пульсаций также получается из условия равновесия (24):

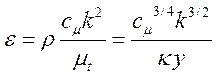.                                       (28)

Вариант 2 (проинтегрированныее значения)

Интегрирование генерации турбулентных пульсаций и диссипации турбулентных пульсаций в пределах турбулентного участка пограничного слоя дает выражения, несколько отличающиеся от узловых (27, 28):

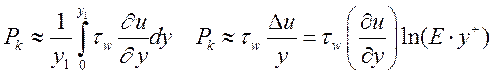                     (29)

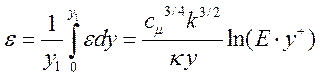
Низкорейнольдсовая k-w модель:

Граничные условия для турбулентных характеристик на твердых стенках (y=0) [M-SST]

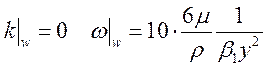                                           (30)

Это условие приемлемо для гладких стенок при y+<3.

k-w модель, автоматическая обработка погранслоя:

Генерация турбулентных пульсаций в ближайшем узле определяется также как и для k-e модели:

                                        

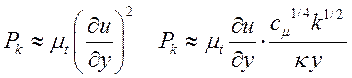
Значение на стенке определяется из условия нулевого диффузионного потока на стенку (23):

Значение удельной диссипации в пристеночном узле находится гладким сопряжением: значений для вязкого w_l и турбулентного w_t подслоя [CFX-WALL]:

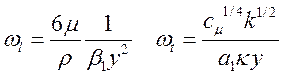                                         (31)

.                                                 (32)

Алгоритм постановки граничных условий на стенке с помощью метода пристеночных функций:

1. Определяется изменение продольной скорости в пределах от стенки до ближайшего узла (9).

2. Рассчитывается безразмерное расстояние до ближайшего узла:

.

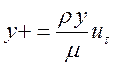Поскольку напряжения на стенке не известны, динамическая скорость находится «смешением» значений для вязкого и логарифмического подслоев [CFX-WALL]:

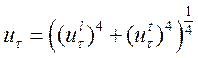  либо                   (33)

Используются следующие выражения:

для вязкого подслоя

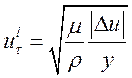                                                    (34)

для равновесного логарифмического подслоя

.                                                    (35)

При использовании высокорейнольдсовых моделей (не способных адекватно описать вязкий подслой), для вычисления y+ применяется ограничение снизу:

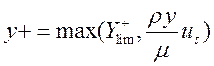.                                       (36)

В качестве ограничивающего значения выбирается точка пересечения линейного и логарифмического профилей .

3. Находится диффузионный поток скорости через грань контрольного объема, совпадающего со стенкой и значение турбулентной вязкости (10). Корректируются коэффициенты конечно-разностной (конечно-объемной) аппроксимации уравнения движения в пристеночном контрольном объеме.