Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 10

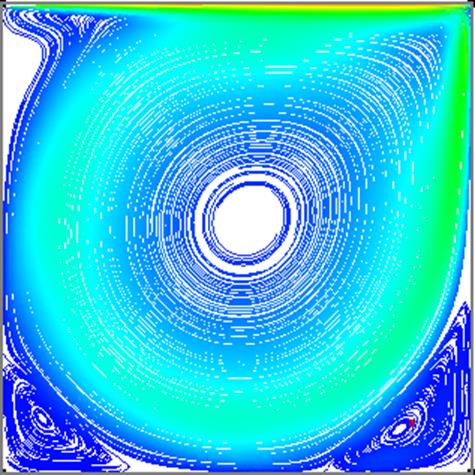
Рис 4 – Линии тока (маркеры). (Re=3200)

Сетка 31×31.

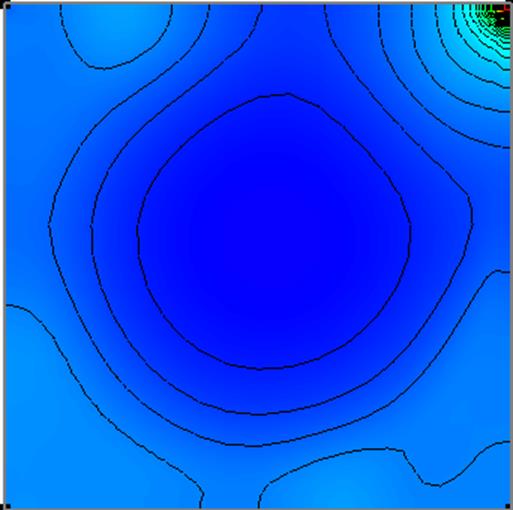
Рис 5 - Изолинии поля давления. (Re=3200)

Сетка 31×31.

Для анализа точности приведем профиль Y компоненты скорости вдоль оси X, в срединном сечении каверны (рисунки 6- 9).

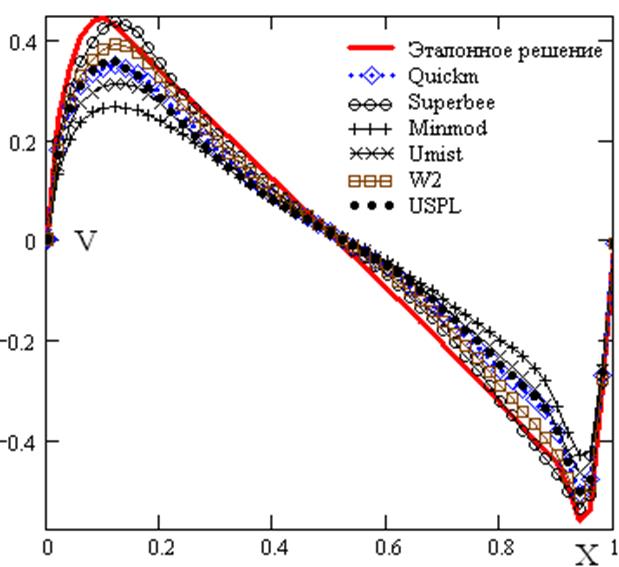
Рис 6. Профиль Y компоненты скорости в среднем сечении каверны.  Re=3200. Сетка 31×31.

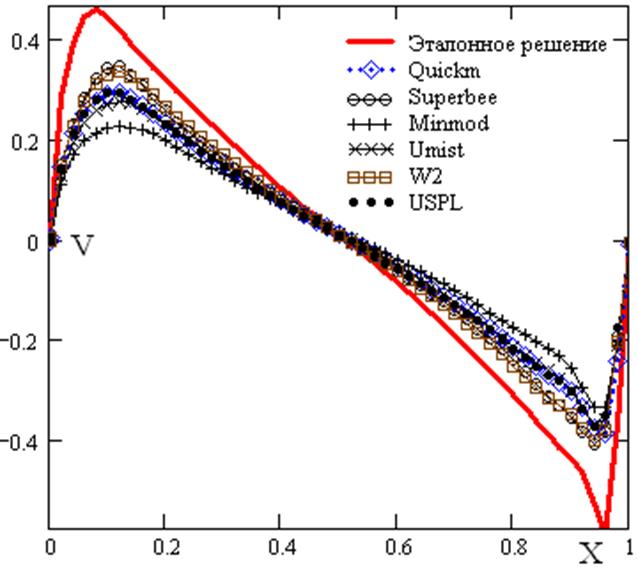
Рис 7. -  Профиль Y компоненты скорости в среднем сечении каверны.  Re=5000. Сетка 31×31

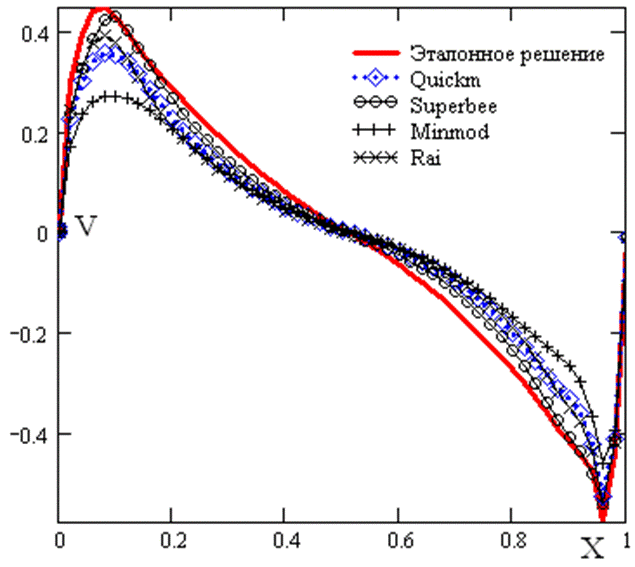
Рис 8. -  Профиль Y компоненты скорости в среднем сечении каверны.  Re=7500. Сетка 51×51.

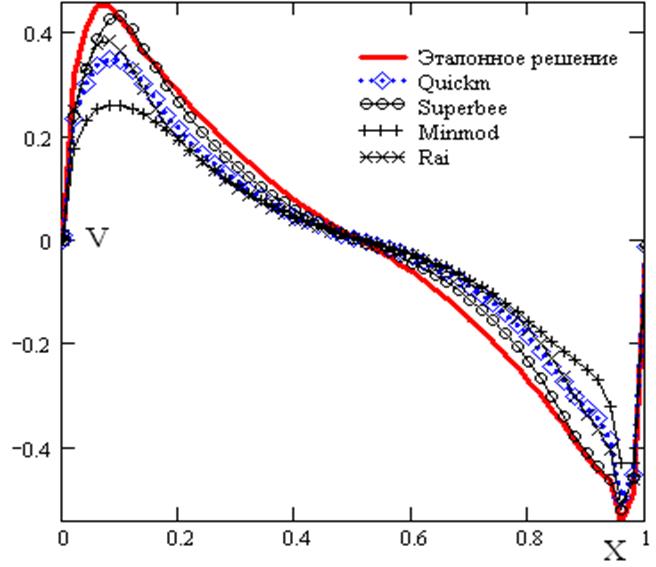
Рис. 9. -  Профиль Y компоненты скорости в среднем сечении каверны. Re=10000. Сетка 61×61.

Прямоугольные каверны

Так же представим несколько расчетов течения жидкости в прямоугольных кавернах.

Линии тока (рис. 10 - 12) в прямоугольных кавернах рассчитаны на сетке 51х51 со сгущением 1.2. Все остальные параметры – те же. Значение числа Рейнольдса во всех случаях равно Re=1000. Форму каверн характеризует отношение её высоты h к длине l.

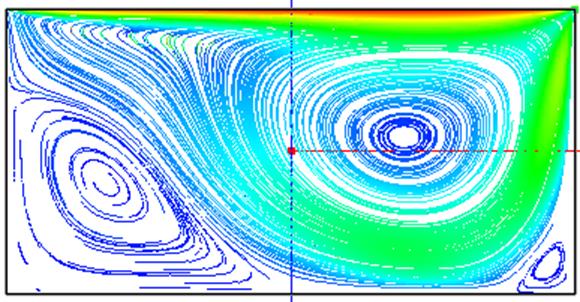
Рис 10 – Линии тока (треки маркеров), Re=1000, h/l=0.5, схема Hibrid

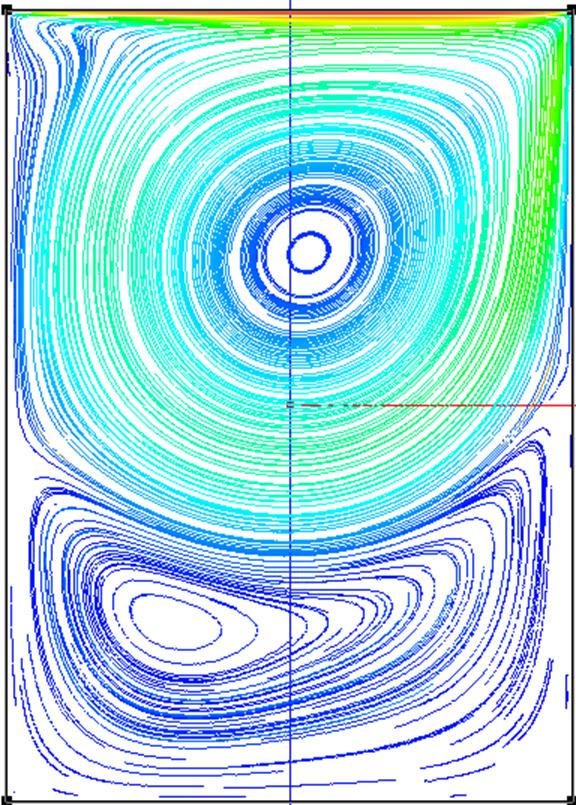
Рис 11 – Линии тока (треки маркеров), Re=1000, h/l=1.4, схема QUICKM

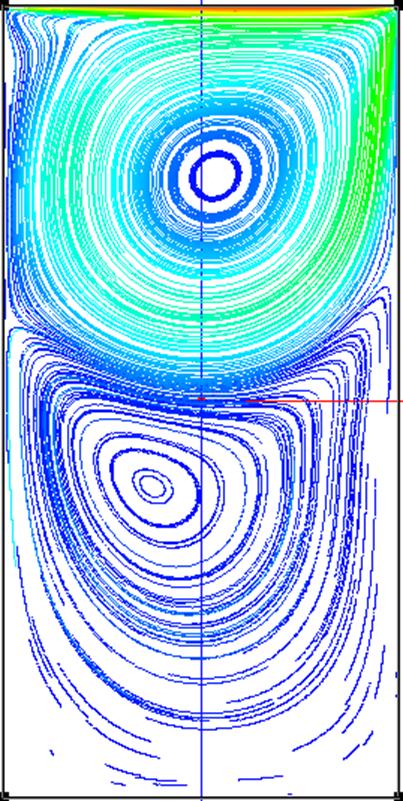
Рис 12 – Линии тока (треки маркеров), Re=1000, h/l=2, схема

6.2. Ламинарное двумерное течение жидкости за обратным уступом.

Геометрические характеристики задачи приведены на Рис. 1, где .

Течение ламинарное, двумерное. Число Рейнольдса, рассчитанное по гидравлическому диаметру входа  и средней скорости изменяется c  по  с шагом . Число Рейнольдса задается изменением вязкости.

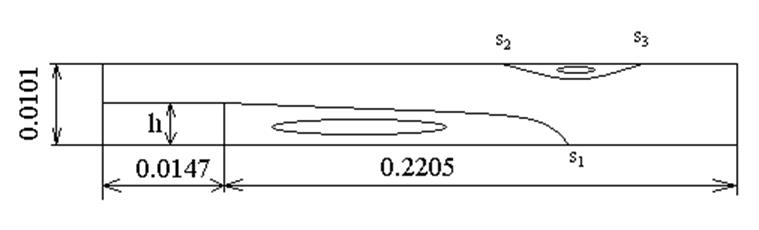
Рис 1. – Геометрия задачи

Сетка, изображенная на Рис. 2, состоит из четырех блоков. В левом нижнем блоке сетка блокируется, верхний левый блок содержит 20 ячеек вдоль канала и 50 ячеек поперек (со сгущением 0,95), правый верхний – 200 ячеек вдоль (со сгущением 1,02) и 50 поперек канала (со сгущением 0,95), правый нижний – 200 ячеек вдоль (со сгущением 1,02) и 50 поперек канала (со сгущением 1,05).

На боковых гранях ставится условие симметрии. На входе задается расход, соответствующий средней скорости . На выходе – условие баланса. Распределение скорости на входе задается параболическим.

Схема аппроксимации – Quickm,

Процедура расщепления – SIMPLEC,

Параметры релаксации для скорости и давления – 0.8, по давлению на границе – 0.9.

Сравнение проводилось по отрезкам s₁, s₂, s₃, которые определялись как точка смены знака продольной компоненты скорости вблизи стенки (таблицы 1 – 3 и Рис. 3). Длины соответствующих отрезков  отнесены к высоте уступа h. Сравнение производится с результатами работы /2/, а также расчетами других авторов, приведенные в /2/ и экспериментальными данными. Как отмечается в /2/, вторая зона рециркуляции появляется при числе Рейнольдса .

На рис. 3 – 5 приведены рассчитанные поля скорости в канале, рис. 6 – 8 – линии тока (треки маркеров), рис. 9 – 11 – изолинии давления для различных чисел Рейнольдса.

Рисунок 2 – Сетка

Таблица 1 – Размеры 1-й зоны рециркуляции s₁/h

Re	100	200	300	400	500	600	700	800
σFlow	2.9	5.0	6.6	8.0	9.2	10.2	10.9	11.5
Расчет из /2/, Chen	3.0	5.1	6.8	8.4	9.5	10.7	11.5	12.3
Эксперимент	3.0	5.1	6.8	8.5	10.1	11.4	13.5	14.8

Таблица 2 – Размеры 2-й зоны рециркуляции s₂/h

Re	500	600	700	800
σFlow	7.8	8.2	8.8	9.2
Расчет из /2/, Chen	8.9	9.2	9.6	10.1
Расчет из /2/, Armaly	7.2	6.7	6.2	5.8
Эксперимент	8.3	9.0	10.4	11.7

Таблица 3 – Размеры 2-й зоны рециркуляции s₃/h

Re	500	600	700	800
σFlow	12.7	15.4	17.8	20.1
Расчет из /2/, Chen	12.2	15.1	17.5	20.0
Расчет из /2/, Armaly	10.7	11.8	11.9	11.8
Эксперимент	14.0	14.9	17.5	20.0

Рисунок 4 – Течение за уступом, Re=400

Рисунок 5 – Течение за уступом, Re=500

Рисунок 6 – Течение за уступом, Re=800

Рисунок 7 – Течение за уступом, линии тока, Re=400

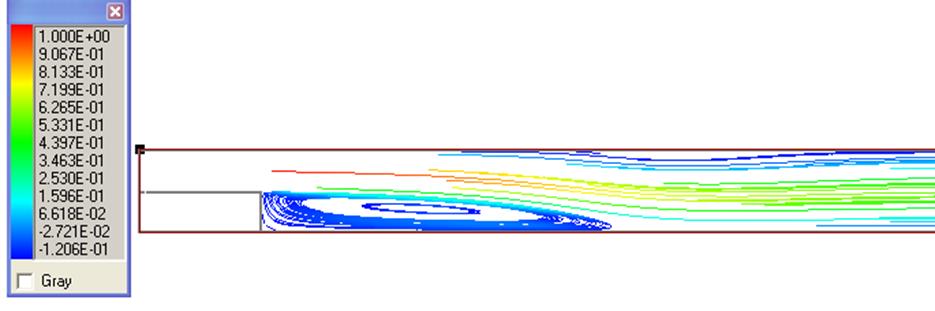
Рисунок 8 – Течение за уступом, линии тока, Re=500

Рисунок 9 – Течение за уступом, линии тока, Re=800

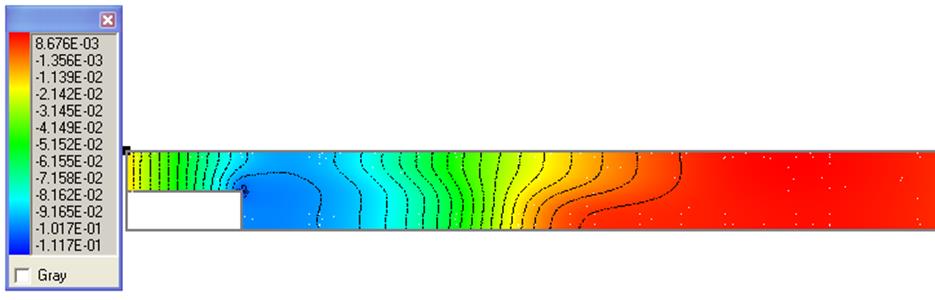
Рисунок 10 – Изолинии давления, Re=400

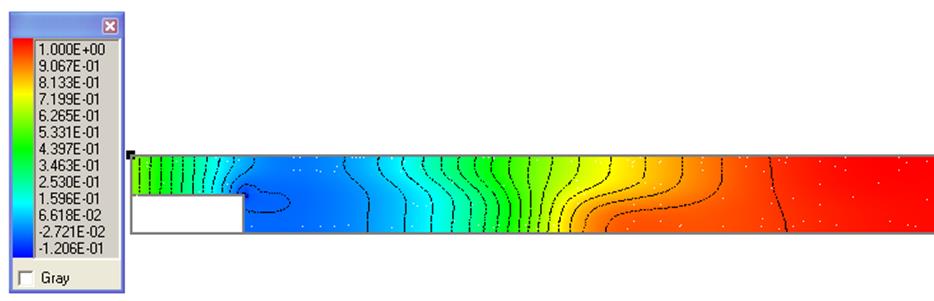
Рисунок 11 – Изолинии давления, Re=500

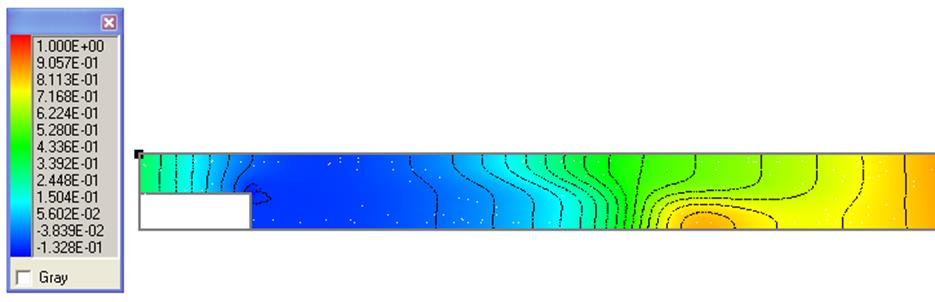
Рисунок 12 – Изолинии давления, Re=800

Литература

1. Chen, Y. S. Viscous flow computations using a second-order upwind difference scheme.

2.  Sang-Wook Kim. A velocity-presure integrated, mixed interpolation, Galerkin finite element method for high Reynolds number laminar flows

6.3. Ламинарное течение жидкости в гибе квадратного сечения

 Описание модели

Канал квадратного сечения 1х1 м, изогнутый на . Длина канала до и после изгиба – по 5 м. Внутренний радиус изгиба – 1.8 м, внешний – 2.8 м. Переменные угла  и радиуса r имеют смысл, показанный на Рис. 1.

Течение ламинарное, расход составляет 1 кг/с. Плотность 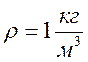, вязкость , число Рейнольдса, рассчитанное по стороне сечения и средней скорости, составляет .

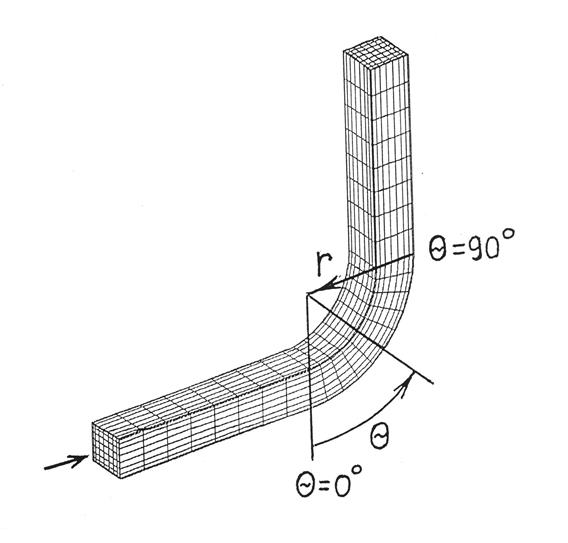
Рис 1. – Геометрия задачи

Расчет проводился на сетке, которая содержит по 50 ячеек в поперечных направлениях и 70 ячеек вдоль канала. Из них по 20 ячеек приходится на участки до и после гиба и 30 ячеек на гиб. Во входном и выходном участках сетка сгущена к гибу (Рис. 2).

Рис 2. – Сетка 51×51×71

Распределение скорости на входе рассчитывается отдельно как установившееся ламинарное течение в прямолинейном канале того же сечения при заданном расходе 1 кг/с.

Результаты расчета

На рис. 3-4 представлены картины течения в продольных сечениях в гибе и, для сравнения, на рис. 5 представлены результаты, полученные Ченом [1]  и др.[2]. Аналогично, картины течения в поперечных сечениях представлены на рис. 7-10.