Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 12

Число Рейнольдса,   Re	10	100	200	300	400
Вязкость,     ,      Па·с	0.1	0.01	0.005	0.00333	0.0025

Таб. 1. Динамическая  вязкость.

4.Расчетная сетка.

Расчеты проводились на сетке (рис.2) состоящей из 81×121×3 узлов (80×120×2 ячеек).

5.Результаты моделирования.

Были выполнены расчеты для соответствующих чисел   Рейнольдса. Картина течения представлена на рисунках 3-7. Сравнение с экспериментом проводилось по доли массового расхода жидкости через верхний канал тройника.

Re	10	100	200	300	400
Массовый расход  на входе, кг/с	0.668	0.668	0.668	0.668	0.668
Массовый расход на верхнем выходе, кг/с	0.350	0.482	0.556	0.591	0.610
Массовый расход на боковом выходе, кг/с	0.318	0.186	0.112	0.077	0.058
Доля массового расхода на верхнем выходе, кг/с	0.524	0.722	0.832	0.885	0.913
Доля массового расхода на верхнем выходе, кг/с (FLUENT.6)	0.524	0.720	0.832	0.886	0.914

Таб.2 Массовые потоки

Рис.2 Расчетная сетка

а)

б)

Рис 3. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 10.

а)

б)

Рис 4. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 100.

а)

б)

Рис 5. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 200.

а)

б)

Рис 6. а) Траектории частиц маркеров.  б) Поле давления. Число Рейнольдса 300.

а)

б)

Рис 7. а) Траектории частиц маркеров. б) Поле давления. Число Рейнольдса 400.

6.6.Свободная конвекция в пространстве между двумя коаксиальными цилиндрами

Kuehn и Goldstein провели экспериментальное изучение естественной конвекции в полости между двумя цилиндрами. Их результаты послужили хорошим тестом для демонстрации возможностей пакета SigmaFlow в моделировании задач тепломассообмена.

Описание задачи

Внутри цилиндра с радиусом 43.6 мм расположен другой цилиндр с радиусом 17.8 мм. Пространство между цилиндрами заполнено воздухом. Так как внутренний цилиндр горячее чем внешний, то в полости между цилиндрами происходит формирование  конвективного течения.

Теплофизические свойства воздуха были взяты при температуре 350К.

Молекулярная вязкость	0.00002081    Па*сек
Коэффициент теплопроводности	0.02967          Дж/м*К
Теплоёмкость	1008               Дж/кг*К
Молекулярный вес	28.966            гр/моль
Число Грасгофа	49500
Число Прантдля	0.0707
Ускорение свободного падения	9.81                м/сек^2

 Граничные условия

Стенки цилиндров считались изотермическими. Внутренний цилиндр имел температуру стеки равную 373К, внешний 327К. На торцах цилиндров ставились условия  симметрии, что позволило трёхмерную задачу свести к двумерной.

Сетка

Сетка состоящая из 61×61×3 узлов представлена на рисунке  1.

Рис 1. Расчетная сетка

Результаты

Изолинии поля температур и поля скоростей показаны на рисунках 2-4. В пространстве между цилиндрами формируется конвективное течение с двумя симметричными вихрями. Под горячим цилиндром образуется застойная область, в которой жидкость почти неподвижна. На изолиниях поля температур виден ярко выраженный эффект стратификации и формирование конвективной колонки. Наблюдается хорошее качественное совпадение поля температур численного расчета и экспериментальной интерферограммы температуры рисунок 3.   

Из графиков 5-5 видно хорошее количественное совпадение численных результатов с экспериментальными.

 

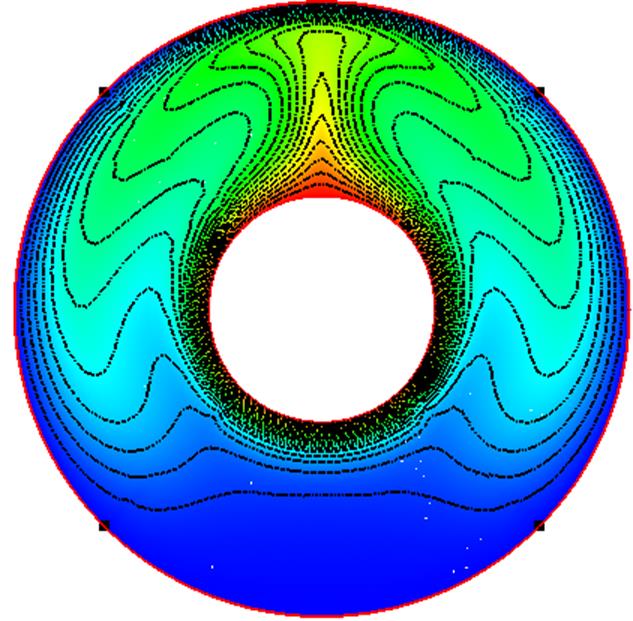
Рис 2. Изолинии поля температур.

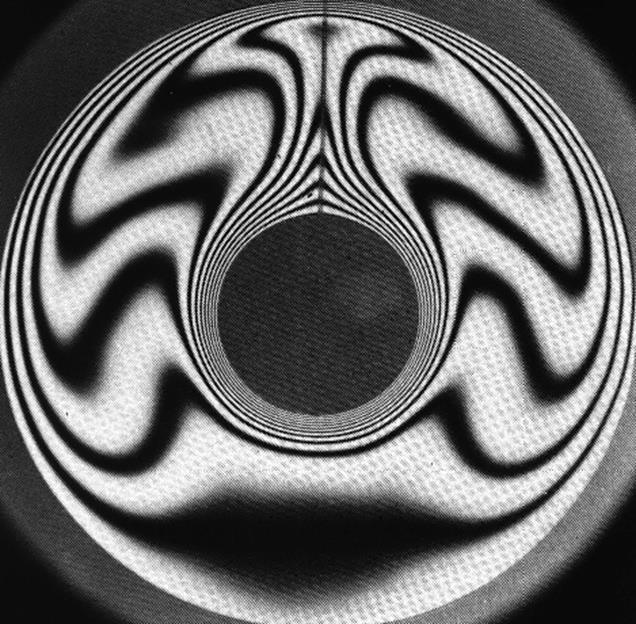
Рис 3. Интерферограмма поля температур.

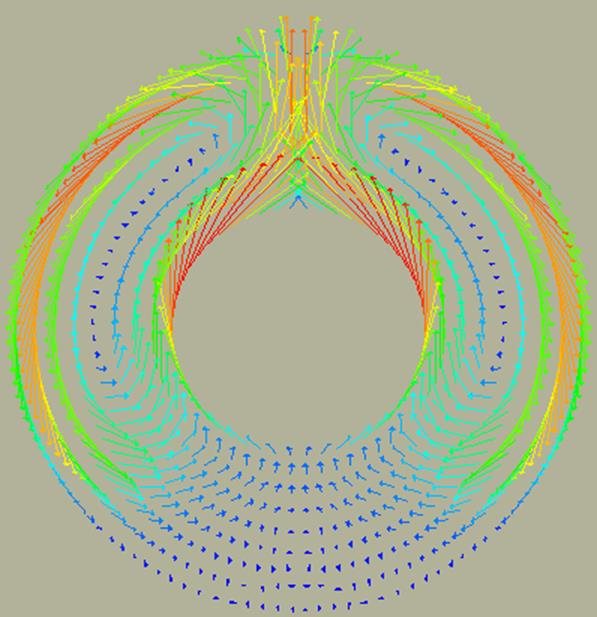
Рис 4 Векторное поле скоростей.

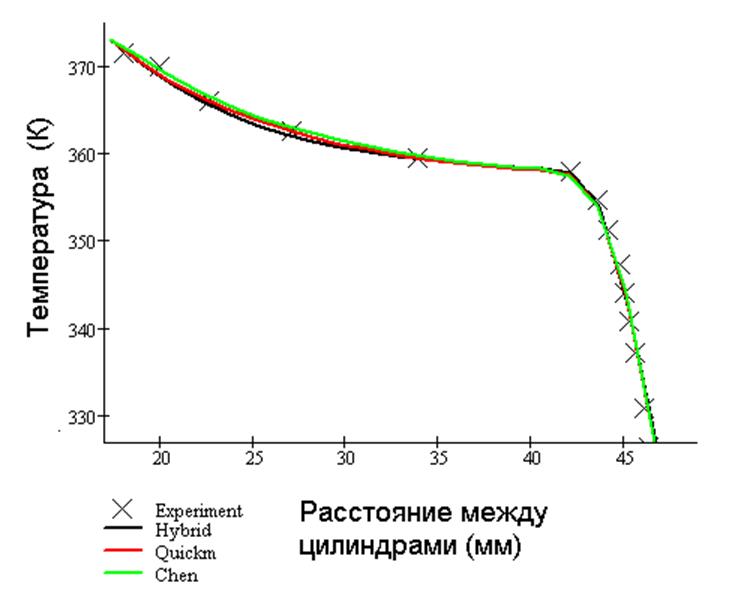
Рис 5. Распределение температуры по радиусу над горячим цилиндром.

(Разными цветами изображены результаты, полученные при помощи различных схем аппроксимации)

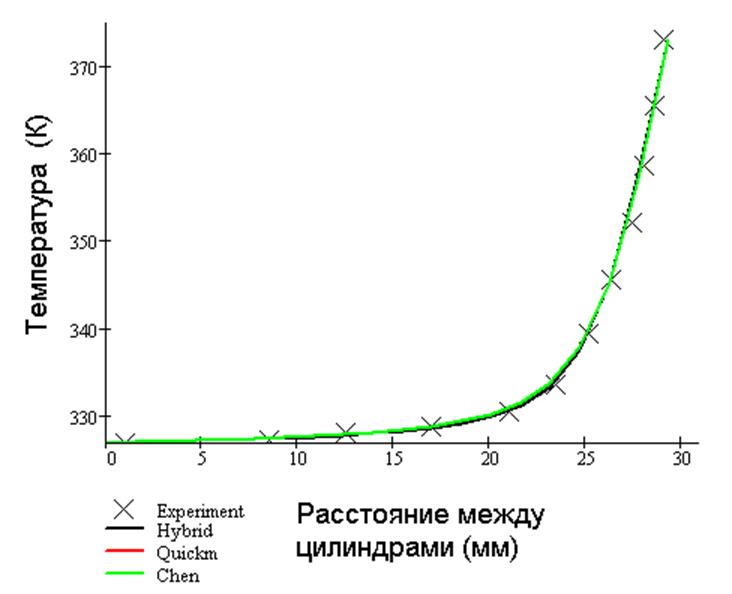
Рис 6.  Распределение температуры по радиусу под горячим цилиндром.

6.7. Свободная конвекция и радиационный теплообмен в квадратной полости

 Введение.

Цель данного теста продемонстрировать возможности пакета «σFlow» в моделировании задач радиационного теплообмена, и сопоставить полученные результаты с пакетом FLUENT.

Описание задачи.

Расчетная область (рис.1) представляет собой квадрат с длиной стороны L=1м. Правая стенка квадрата имеет температуру 2000 К, левая стенка 1000 К. Верхняя и нижняя стенки считались адиабатическими. Гравитация направлена вниз. Стенки квадрата считались абсолютно черными. 

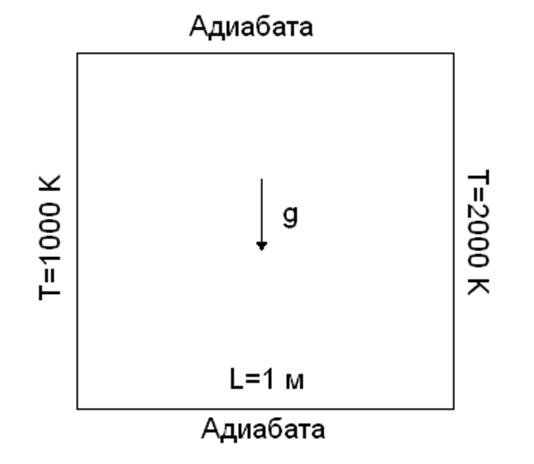
Рис.1 Расчетная область

Физические параметры.

Плотность	1000                  кг/м3
Молекулярная вязкость	0.001                 Па*сек
Теплоемкость	11030                Дж/кг*К
Коэффициент теплопроводности	15.309               Вт/м*К
Изобарный коэффициент расширения	0.00001             1/К
Число Релея	500000
Число Планка	0.02
Коэффициент поглощения среды	0.2
Ускорение свободного падения	-0.0000696    м/сек2
Число Прандтля	0.71

Граничные условия.

Нижняя и верхняя стенки считались адиабатическими. На боковых стенках задавалась постоянная температура, на правой 2000 К, на левой 1000 К.

Коэффициент поглощения материала стенок был равен 1. Для вырождения задачи в двумерную, на торцах квадрата ставились условия симметрии.

Сетка.

Расчетная сетка состояла из 50×50 узлов, и имела сгущение к стенкам.

Рис.2 Расчетная сетка.

Результаты.

Все расчеты проводились при помощи схемы QIUCKM второго порядка аппроксимации.