Другие предметы \ Методы вычислительной гидродинамики

Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 6

Широко известная в CFD квадратичная противопоточная интерполяция (QUICK) предложенная Леонардом.

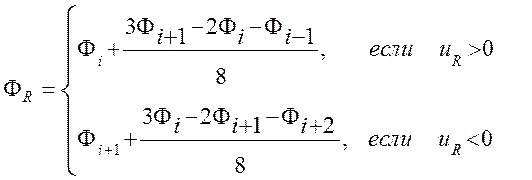                                             (3.3.5)

Данная схема имеет второй порядок аппроксимации и обладает высокой скоростью сходимости, чем и объясняется ее широкое применение при решении задач гидродинамики и тепломассообмена.

Ниже приведены еще несколько противопоточных схем высокого порядка.

Схема третьего порядка (Chen)

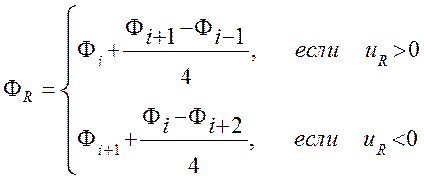                                                  (3.3.5)         

Схема третьего порядка (KWMR)

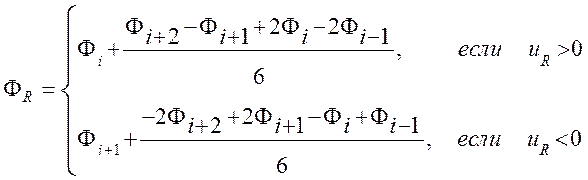                           (3.3.6)

Схема четвертого порядка порядка (Peric)

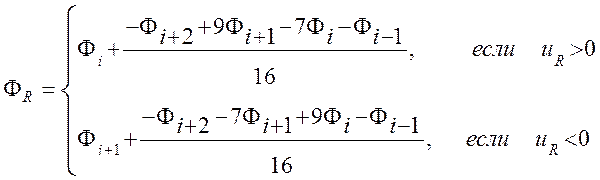                          (3.3.7)

Схема пятого порядка (Rai)

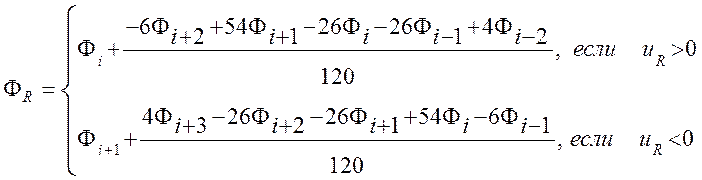                    (3.3.8)

Противопоточные схемы высокого порядка с ограничением потока

После публикации Колгана  в 1972 начало интенсивно развиваться новое поколение схем аппроксимации конвективного потока, которые в последствии получили названия TVD-схемы (Total Variation Diminishing).

Несмотря на то, что TVD-схемы разрабатывались, прежде всего, разрывных решений газовой динамики, они имеют большое будущее и в области численного моделирований гладких решений задач несжимаемой жидкости. При этом основным положительным свойством этих схем является монотонность получаемого решения, которое достигается благодаря  специальной методике расчета конвективных потоков через грани контрольного объема.

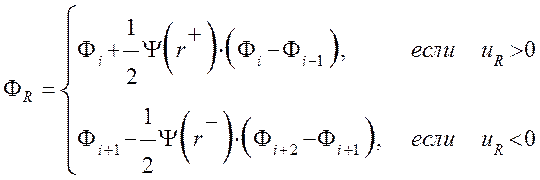
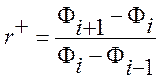
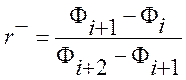                                                             (3.3.9)

где Ψ(r) –функция ограничитель, которая отвечает за свойства полученной  схемы.  Функция ограничитель Ψ(r) строится таким образом, чтобы давать  высокий порядок аппроксимации там, где это возможно, и в тоже время гарантировать выполнение критерия ограниченности разностной схемы.

Таблице 3.3.1. приведены реализованные в “sFlow”  схемы аппроксимации с ограничением потока.

Таблица 3.2.2.2

Схема аппроксимации

Ограничитель

MINMOD

UMIST

SUPERBEE

Van Leer

Van ALBADA

W2

,,

MUSCL

USR-k

3.2.2. Дискретизация обобщенного уравнения на криволинейных сетках

Записанные выше соотношения представлены в физическом пространстве в декартовой  системе координат, в которой координатные линии и поверхности пересекаются под прямым углом. Однако при моделировании течения в технологических установках часто приходится рассматривать расчетные области со сложной геометрией, у которых граничные поверхности не совпадают с координатными поверхностями. Поэтому целесообразно записать исходные уравнения в обобщенных криволинейных координатах, согласованных с границами расчетной области. В этом случае удается более точно задать граничные условия. Для обобщенного уравнения  переход к криволинейным координатам (x, h, z) дает:  

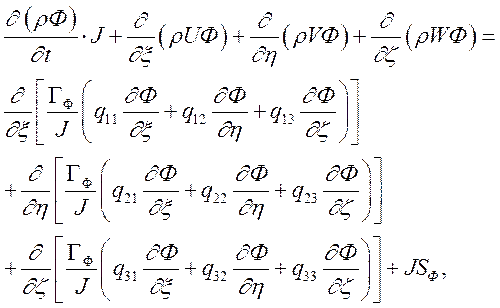                    (3.2.2.1)

где     J - якобиан преобразования;

         U, V, W - контравариантные составляющие скорости;

         - функции метрических коэффициентов;

                       

                               

                      

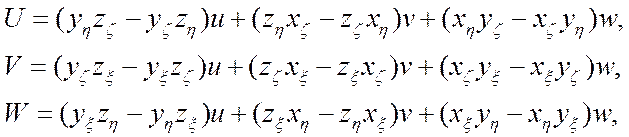
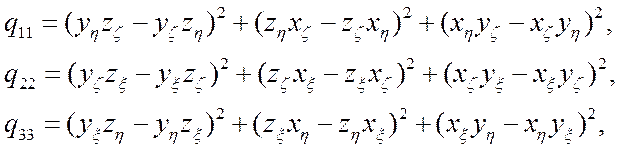
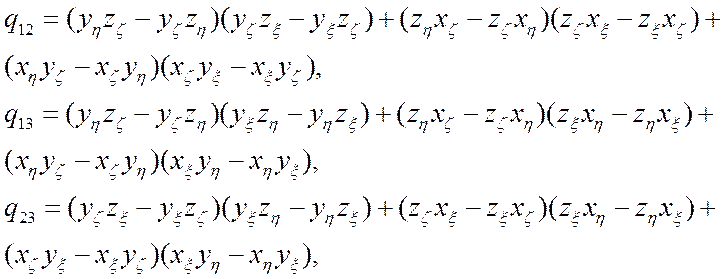          (3.2.2.2)

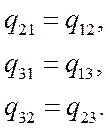
В преобразованном  математическом  пространстве для упрощения записи все расстояния между координатными узлами (x, h, z) выбираются единичными. Производные  определяются численно с использованием центральных разностей второго порядка точности.

Построение  конечно-разностного аналога исходных дифферинциальных уравнений на криволинейных неортогональных расчетных сетках не имеет принципиальных отличий от рассмотренного выше вывода разностных соотношении для декартовых сеток. Записанное в криволинейной, согласованной с границами расчетной области системе координат (x, h, z) обобщенное уравнение (3.2.1) интегрируется при помощи метода контрольного объема.

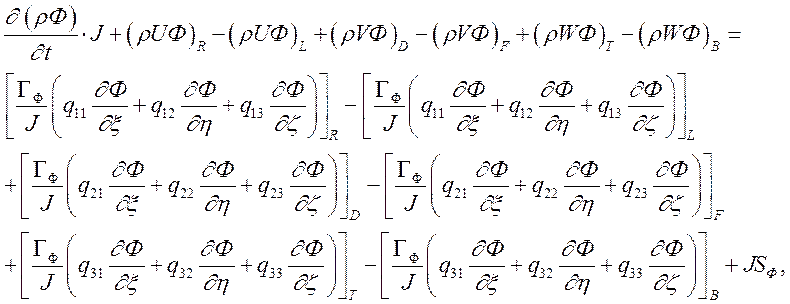(3.2.2.3)

Члены, содержащие смешанные производные вычисляются при помощи значений Ф полученных на предыдущей итерации (k).

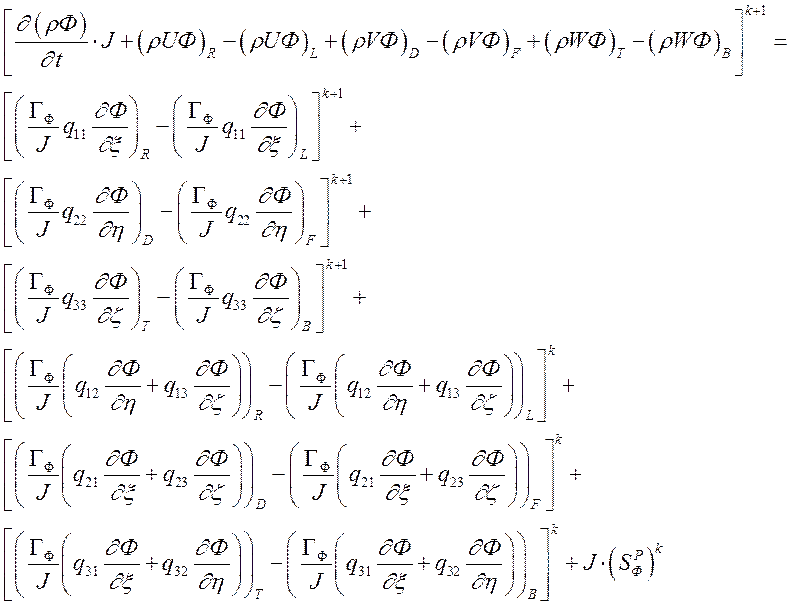(3.2.2.4)

Дальнейшая дискретизация конвективно-диффузионных потоков и нестационарного члена производится  при помощи описанных в 3.2 - 3.4 способов.

Аппроксимация смешанных производных осуществляется при помощи центрально-разностной схемы второго порядка, например:

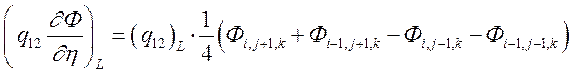                                    (3.2.2.5).

3.3. Дискретизация нестационарного члена

Дискретизация по времени в “sFlow” осуществляется неявным способом, в программе реализованы следующие схемы аппроксимации временной производной.

Неявная схема Эйлера первого порядка:

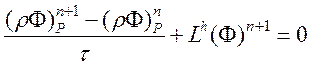                                                                            (3.3.1)

 Неявная схема Пейре второго порядка:

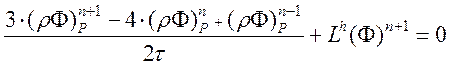                                                         (3.3.2)

где -шаг по времени, -разностный оператор полученный после дискретизации уравнения (3.1) по пространству.

3.4. Связь полей скорости и давления (SIMPLE алгоритмы)

При решении уравнений Навье-Стокса в естественных переменных для несжимаемой жидкости возникают трудности в связи со сложностью интерпретации взаимодействия давления и составляющих скорости. Это обусловлено тем, что давление как искомый параметр в исходных дифференциальных уравнениях не выражается явным образом. Подход с расщеплением исходной задачи, реализованный в процедуре SIMPLE, предложенной Патанкаром и Сполдингом, позволяет разрешить эту проблему [12]. Согласно этой процедуре из дискретных аналогов уравнений количества движения и неразрывности выводится уравнение для поправки давления. Используя решение уравнения для поправки давления, производится коррекция поля скорости и давления. На практике используется модификация описанного выше алгоритма - SIMPLEC-процедура, применение которой приводит к значительному повышению эффективности расчетов.

Рассмотрим алгоритм расщепления для нестационарных уравнений Навье-Стокса:

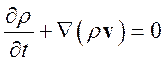                                                          (3.4.1)

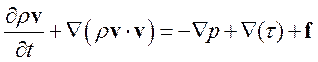,                                   (3.4.2)

где тензор вязких напряжений

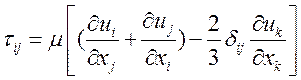.                                     (3.4.3)

Рассматриваются течения с сильной связью полей давления и плотности. Количественно эту связь описывает параметр:

Скачать файл