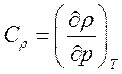 (3.4.4).
(3.4.4).
К течениям с взаимосвязью давления и плотности относятся сжимаемые течения газа, с параметром «сжимаемости»:
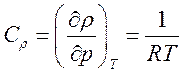 ,
,
и кавитационные течения жидкости. Часто для кавитационных течения принимается пропорциональность параметра связи давление-плотность объемной доли паровой фазы:
![]() . (3.4.5)
. (3.4.5)
Вывод алгоритма расщепления
В уравнении импульса выделим нестационарный член и градиент давления, остальные слагаемые (конвекция, тензор напряжений и объемная сила) объединим в оператор L:
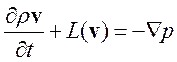 . (3.4.6)
. (3.4.6)
Запишем уравнение переноса импульса для промежуточной скорости с давлением с предыдущего временного слоя и уравнение переноса импульса, связывающее скорость и давление на текущем временном слое:
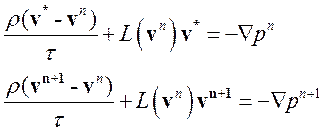 (3.4.7)
(3.4.7)
Здесь временная производная аппроксимирована с первым порядком точности. Вычитая из второго уравнения первое
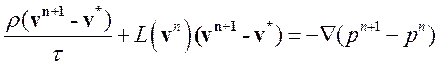 (3.4.8)
(3.4.8)
и пренебрегая слагаемым
![]() ,
,
(итерационный учет этого члена можно организовать методом PISO)
получаем уравнение коррекции скорости
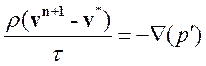 (3.4.9)
(3.4.9)
на основе поправки давления
![]() . (3.4.10)
. (3.4.10)
Действуем оператором дивергенции на уравнение коррекции скорости (3.4.9)
![]()
и, используя аппроксимацию уравнения неразрывности (4.1), записанного для n+1-го временного слоя
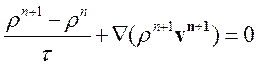 , (3.4.11)
, (3.4.11)
получаем уравнение поправки давления:
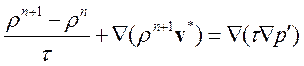 . (3.4.12)
. (3.4.12)
С использованием поправки плотности, введенное аналогично поправки давления
![]()
уравнение для поправки давления можно записать в виде:
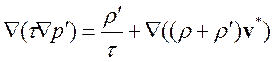
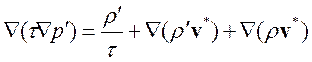 .
.
Учет взаимосвязи полей давления и плотности
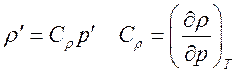 (3.4.13)
(3.4.13)
приводит к модификации уравнения для поправки давления:
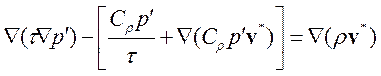 . (3.4.14)
. (3.4.14)
Процесс вычислений для описываемого одношагового безитерационного метода разбивается на 3 этапа:
1. Определение промежуточной скорости по давлению с предыдущего слоя
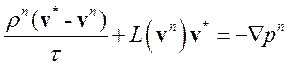 (3.4.15)
(3.4.15)
2. Вычисление давления на основе уравнения для поправки давления
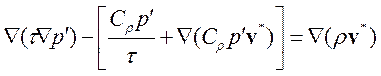 (3.4.16)
(3.4.16)
![]() (3.4.17)
(3.4.17)
3. Коррекция скорости
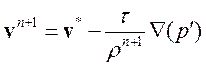 (3.4.18)
(3.4.18)
Этот процесс реализует идею расщепления по физическим параметрам: на первом этапе производится учет конвективно-диффузионного оператора L и силы давления, на втором этапе выполняется коррекция полей скорости и давления для выполнения закона сохранения массы (уравнения неразрывности).
Построенная разностная методика позволяет получать решение нестационарной задачи или же решение стационарной задачи методом установления. В том случае, если нестационарные эффекты не представляют интереса, целесообразно модифицировать численный алгоритм для уменьшения времени счета. Модификация состоит в том, что t выступает уже не в качестве постоянного временного шага, а в качестве схемного параметра, зависящего от течения в данном контрольном объеме. Выбор этого параметра осуществим на основе рассмотрения неявных итерационных схем для стационарных уравнений переноса импульса.
Запишем дискретный аналог стационарного уравнения количества движения
![]() (3.4.19)
(3.4.19)
и применим операцию нижней релаксации:
![]() ,
,
сводящуюся к изменению разностного оператора:
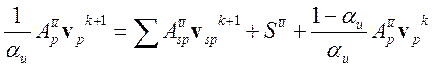 , (3.4.20)
, (3.4.20)
здесь
![]() - скорость на k-ой
итерации и коэффициент нижней релаксации.
- скорость на k-ой
итерации и коэффициент нижней релаксации.
Разностная схема для нестационарного уравнения количества движения (3.4.2) имеет следующий вид:
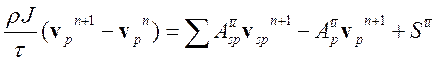
или
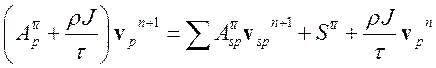 (3.4.21)
(3.4.21)
Сравнение нестационарного и стационарного вариантов приводит к выражению для t согласованного с операцией нижней релаксации:
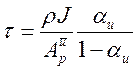 . (3.4.22)
. (3.4.22)
Приведем выражения для t, использующиеся в процедуре SIMPLE
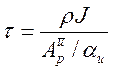 (3.4.23)
(3.4.23)
и в процедуре SIMPLE-C
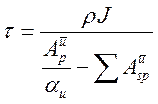 . (3.4.24)
. (3.4.24)
В стационарном расчете при нахождении давления на втором шаге для усиления устойчивости (но с потерей скорости сходимости) возможно введение нижней релаксации:
![]() . (3.4.25)
. (3.4.25)
Для одношагового нестационарный расчета можно предложить вычисление временного шага по аналогии с формулой (1.22)
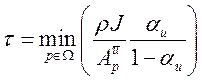
или, введя понятие CFL
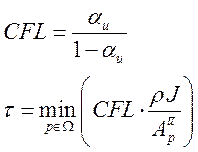
Обобщение алгоритма
Для увеличения точности и устойчивости метода расщепления обобщим алгоритм для варианта с внутренними итерациями. Для этого в уравнении импульса (1.15) заменим давление и плотность с предыдущего временного слоя на давление и плотность с текущего временного слоя, но с предыдущей итерации:
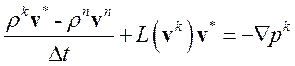 (3.4.26)
(3.4.26)
Здесь для временного шага введено обозначение Dt.
Поправка давления теперь имеет смысл коррекции давления на текущем временном слое:
![]() (3.4.27)
(3.4.27)
Запишем уравнение поправки давления в виде:
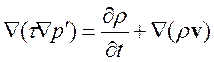 .
.
В данном случае t выступает на в качестве временного шага, а в качестве схемного параметра, выбор которого позволяет ускорить сходимость внутренних итераций. Аппроксимируем временную производную и введем поправку плотности аналогично поправки давления:
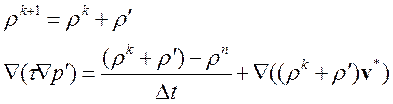 (3.4.28)
(3.4.28)
Объединяя слагаемые коррекции и вводя связь полей плотности и давления, получаем окончательный вид уравнения для поправки давления:
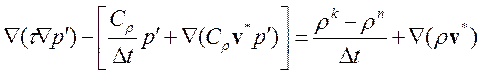 (3.4.29)
(3.4.29)
Коррекция скорости выполняется как и в случае безитерационного метода (1.18):
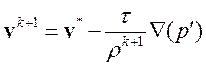 (3.4.30)
(3.4.30)
Сделанное обобщение позволяет использовать схемы высокого порядка для аппроксимации временных производных в уравнениях импульса и неразрывности. Для примера запишем популярную трехслойную схему Пейре второго порядка аппроксимации:
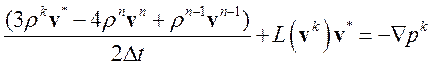 (3.4.31)
(3.4.31)
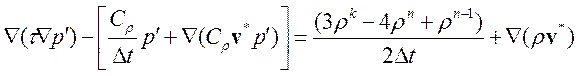
Итерационный процесс вычислений на каждом временном слое состоит из трех этапов:
1. Вычисление промежуточной скорости:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.