Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 8

Почему в случае  интенсивность с глубиной спадает по экспоненте? Возможно ли провести аналогию с экспоненциальным поглощением по закону Бугера-Ламберта-Бера? Какая волна наблюдается: бегущая или стоячая? Почему пучности поля сосредоточены на границах слоев?

Почему на границе запрещенной зоны поле в кристалле образует стоячую волну, а интенсивность локализуется в середине кристалла? Почему на низкочастотной границе запрещенной зоны пучности поля сосредоточены в слоях с меньшим коэффициентом преломления, а на высокочастотной границе запрещенной зоны – в слоях с большим коэффициентом преломления?

Задача 3.6.10. Полоса пропускания. Резонансы

В задаче 3.6.10 найдите первую полосу пропускания (между первой и второй запрещенными зонами). В ней найдите резонансные частоты, на которых отражение отсутствует. Как количество резонансных частот соответствует количеству периодов фильтра (фотонного кристалла)? Почему крайние резонансы ýже, а провалы между резонансами шире?

Постройте поле в кристалле для каждой из резонансных частот.

Задача 3.6.11. Настроенный фильтр

Оптической толщиной слоя называется его толщина, умноженная на коэффициент преломления, или количество длин волн, укладывающееся в слое, набег фазы волны.

В задаче 3.6.10 увеличьте вдвое толщину воздушных зазоров. Постройте в частотном спектре пропускания первые пять запрещенных зон. Они выглядят одинаково. Такую структуру называют настроенным фильтром, или фильтром равной длины волны (полуволновым, четвертьволновым). Это связано с тем, что оптическая толщина каждого слоя (пластинок и воздушных зазоров) одинакова.

Объясните связь равенства оптических толщин слоев с равенством запрещенных зон.

Задача 3.6.12. Глубина запрещенной зоны

Логарифмический спектр – зависимость от частоты логарифма пропускания или отражения, выражающегося в децибелах(дБ): . Падению интенсивности в 10 раз соответствует  дБ, а в 1000 раз –  дБ.

Для предыдущей задачи покажите, что логарифмический спектр запрещенной зоны представляет собой параболу.

Для настроенного и ненастроенного фотонных кристаллов в задачах 3.6.10 и 3.6.13 сравните:

а) глубину запрещенной зоны (высоту параболы);

б) пики отражения в полосе пропускания.

Объясните разницу.

Задача 3.6.13 Неслоистая среда

Используя метод трансфер-матрицы, постройте спектр пропускания среды с коэффициентом преломления , , разбивая среду на 100 слоев толщиной  и приближенно полагая коэффициент преломления в каждом слое постоянным. Почему высшие запрещенные зоны мельчают и пропадают? Проведите аналогию такой структуры с самосборкой фотонного холестерического жидкого кристалла.

Задача 3.6.14 Дефект

Фотонный кристалл состоит из десяти одинаковых плоских алмазных пластинок с коэффициентом преломления  толщиной  каждая, расположенных параллельно друг другу с воздушными зазорами толщиной  каждый. Чтобы создать дефектный слой, пятый по счету воздушный зазор, находящийся посередине кристалла, увеличили вдвое. В спектре первой запрещенной зоны появилась область пропускания, называемая дефектной модой.

Как изменяется положение дефектной моды с изменением толщины дефектного слоя?

Что будет, если выбрать нецентральный дефектный слой?

Как распределено поле внутри кристалла на частоте дефектной моды?

Задача 3.6.15 Вырождение и расщепление частот дефектных мод

Одномерный фотонный кристалл состоит из 15 периодов. Пятнадцать одинаковых плоских алмазных пластинок с коэффициентом преломления  толщиной  каждая, расположенных параллельно друг другу с воздушными зазорами с показателем преломления  толщиной  каждый. В такой фотонный кристалл внедили два дефекта, увеличив пятый и десятый воздушные зазоры вдвое (см. рис.).

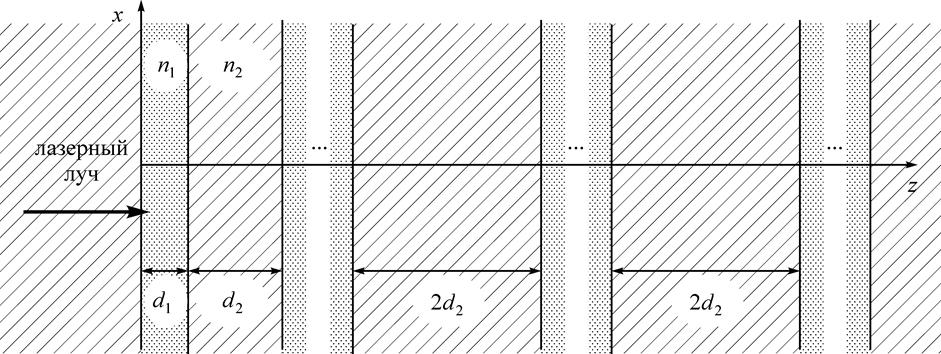
Рис. Конечный фотонный кристалл с двумя дефектами.

а) Методом трансфер-матрицы провести расчет спектра пропускания фотонного кристалла в случае нормального падения света на образец.

б) Найти распределение интенсивности поля в фотоном кристалле для частот дефектных мод.

в) Дефектные слои представляют собой одинаковые микрорезонаторы, однако частоты в запрещенной зоне, соответствующие их резонансам разошлись, произошло снятие вырождения. Объясните его механизм. Сопоставьте данное явление с изменением частоты нормальных колебаний при взаимодействии двух одинаковых математических маятников, подвешенных на одну провисающую веревку.

г) Как изменятся пики пропускания, если дефекты переместили в третий и двенадцатый воздушные зазоры.

Задача 3.6.16 Дефектная подрешетка

Фотонный кристалл состоит из двадцати пяти одинаковых плоских алмазных пластинок с коэффициентом преломления  толщиной  каждая, расположенных параллельно друг другу с воздушными зазорами толщиной  каждый. Каждый пятый воздушный зазор увеличили вдвое. В спектре первой запрещенной зоны появилась дефектная полоса пропускания.

Сколько резонансов наблюдается в дефектной полосе пропускания. Для объяснения воспользуйтесь тем фактом, что структура помимо основного периода в 150 нм модулируется периодом в 800 нм, дефекты образуют подрешетку.

Задача 3.6.17. Угол падения

Фотонный кристалл с числом слоев , включает дефектный слой, расположенный в центре слоистой среды. Толщины слоев  мкм, показатели преломления соответственно , ; для дефекта  мкм, . Показатель преломления среды, окружающей кристалл, .

Получить зависимость коэффициента пропускания фотонного кристалла с дефектом от частоты  и угла падения  для ТЕ и ТМ мод.

В случае ТМ моды найти угол Брюстера, при котором исчезает френелевское отражение на границах раздела.

Уменьшите коэффициент преломления дефекта до . Получите спектр пропускания при углах, бóльших угла полного внутреннего отражения. Проведите аналогию с туннельным эффектом.

Задача 3.6.18. Распределенные и сосредоточенные характеристики системы

Законы теории колебаний носят математический характер и потому открывают удивительное подобие физических процессов, наблюдаемых в совершенно различных системах, описываемых одними уравнениями.

Так, математический маятник, пружинный осциллятор и электрический контур емкости-индуктивности описываются одним и тем же гармоническим уравнением.