Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 7

Раздел 5. Волноводы на основе фотоннокристаллических структур

Задача 2.5.1. Возмущенный диэлектрический планарный волновод

Пусть возмущение диэлектрической проницаемости планарного волновода записывается в виде

                                         

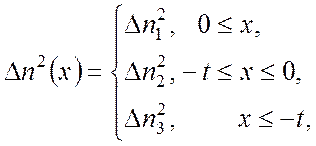
где , и  – постоянные величины (могут быть комплексными при наличии усиления или поглощения).

а) Покажите, что поправка к постоянной распространения дается выражением

                                   ,

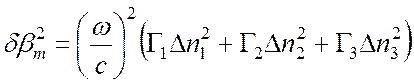где

                                            , ,

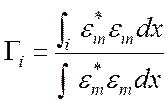причем интегрирование осуществляется по i-й среде. Величины Г определяют долю мощности, которая протекает в соответствующей среде.

б) Для планарного волновода с фиксированной толщиной  постоянные распространения можно рассматривать как функции величин , и . Таким образом, для  можно записать

                                  .

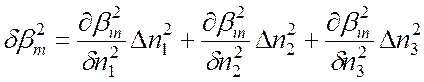Функция  входит неявно в выражение (11.14). Покажите непосредственно из выражения (11.14), что

                                            , .

Задача 2.5.2

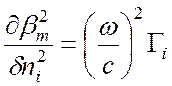Пусть имеется волновод на основе пленки GaAs толщиной 1 мкм, выращенный на подложке из AlGaAs. Показатели преломления при  мкм имеют следующие значения: .

а) Установите, используя рис. 12.3 (раздел 5), чему равно число локализованных мод в этой пленке.

б) Каким углам падения  соответствуют эти эффективные показатели преломления (). Какая из мод имеет наибольший показатель преломления и угол падения?

Задача 2.5.3

Объяснить механизм призменого метода ввода излучения в тонкопленочный планарный волновод (см. лекцию 2).

Задача 2.5.4

Частным случаем волноводной структуры изображенной на рис. 12.2 (раздел 5) является структура с . Используя выражение для полей (12.12) и модовое условие (12.14) показать, что поверхностная ТЕ-мода не может существовать на границе раздела двух однородных сред.

Задача 2.5.5

Показать, что существуют такие решения уравнений Максвелла, которые соответствуют распространению поверхностных волн ТМ-типа только вдоль границы раздела между двумя немагнитными средами с экспоненциальным затуханием по мере удаления от границы раздела. Определить связь между частотой и волновым вектором поверхностной волны, а также характер ее поляризации.

Задача 2.5.6

Объяснить механизм волноводного распространения света через Г-образную цепочку дефектов в двумерном фотонном кристалле, используя результаты решенной задачи 3.6.16.

Модуль 3
Исследование оптических свойств фотонных кристаллов

Раздел 6. Спектры пропускания фотонных кристаллов с дефектами решетки

Задача 3.6.1. Плоские волны

В лекциях, в параграфе 5.2 «Одномерные периодические среды» приводится бесконечная система уравнений (5.17) для плоских волн, которые могут распространяться в бесконечной периодической среде. Эта система имеет аналитическое решение (5.27) при учете двух основных плоских волн. Численно уточните данное решение, учитывая пять основных плоских волн с амплитудами , , . Как сильно изменяются дисперсионные кривые на рис. 5.1, б при учете большего числа плоских волн?

Задача 3.6.2

Обобщите результаты параграфа 5.2 лекций на случаи 2-мерной и 3-мерной периодической слоистой среды. Какие новые особенности возникают при увеличении размерности.

Задача 3.6.3.

Систему уравнений (5.24), (5.25) запишите в матричном виде , где  – единичная матрица размера 2х2. Численно найдите собственные числа  и собственные вектора  матрицы . Перебирая различные , постройте дисперсионную кривую . В трех случаях  постройте пространственный профиль волны . Обобщите задачу, учитывая пять основных плоских волн с амплитудами , , .

Задача 3.6.4. Матрица переноса

Пусть в воздушную среду с коэффициентом преломления  помещена плоская алмазная пластинка с коэффициентом преломления  толщиной . На пластинку под прямым углом падает желтый свет с длиной волны  и амплитудой электрической напряженности .

В лекциях, в параграфе 6.1 «Периодические слоистые среды» приводится матрица (6.11) с компонентами (6.12), которая поле в слое 1 элементарной ячейки преобразует в поле в слое 1 соседней элементарной ячейки. Воспользуйтесь этой матрицей, чтобы рассчитать прошедшее и отраженное поля.

Задача 3.6.5. Четвертьволновая пластинка

Решите предыдущую задачу для случая . Объясните, почему увеличилось отражение. Считайте, что коэффициент преломления алмаза не зависит от длины волны.

Задача 3.6.6. Провалы в спектре

Пропусканием фильтра называется отношение интенсивности прошедшей волны к интенсивности падающей волны. Спектром пропускания называется зависимость пропускания от длины волны.

В условиях предыдущей задачи численно постройте и физически объясните спектр пропускания алмазной пластинки в диапазоне длин волн: а) видимого диапазона , б) ультрафиолетового диапазона . Объясните немонотонное изменение пропускания с длиной волны.

Задача 3.6.7. Унимодальность и след

При помощи уравнений (6.9) и (6.10) лекций постройте матрицу переноса, связывающую поля в слое 2 соседних элементарных ячеек. Убедитесь, что матрица унимодулярна и ее след совпадает со следом матрицы (6.12) для слоя 1.

Задача 3.6.8. Многослойный фильтр

Световой фильтр (фотонный кристалл) состоит из пяти одинаковых плоских алмазных пластинок с коэффициентом преломления  толщиной  каждая, расположенных параллельно друг другу с воздушными зазорами толщиной  каждый.

Постройте спектр отражения фильтра, возводя матрицу переноса в пятую степень. Сравните полученный результат с аналитическим решением (6.42) лекций. Выберите характерный диапазон частот, определите границы первой запрещенной зоны  и центральную частоту , на которой отражение максимально. Покажите, что запрещенная зона зеркально симметрична: .

Задача 3.6.9. Поле в фотонном кристалле. Запрещенная зона

Метод трансфер-матрицы позволяет найти поле не только на входе и выходе слоистой среды, но и в произвольной точке внутри среды. В последнем случае следует перемножать не все матрицы слоев, а лишь начиная от выхода и заканчивая интересующей точкой среды.

Опираясь на вышесказанное, в предыдущей задаче численно найдите распределение интенсивности поля в фотонном кристалле  для случаев .