Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 10

где  – групповая скорость, . Найдите огибающую импульса со спектральным распределением, соответствующим гауссову импульсу

                                                      (2)

и определите зависимость ширины огибающей от времени. При расчетах можно использовать следующий интеграл:

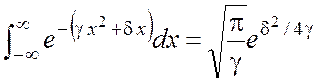                                          .              (3)

В этом интеграле вещественная часть параметра должна быть положительной.

Решение

Распространение лазерного импульса можно описать, если представить импульс в виде суммы многих плоских волн, являющихся решениями уравнений Максвелла (см. лекцию 2):

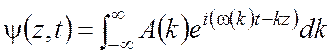                                         .             (4)

Под скалярной амплитудой  подразумевается одна из составляющих векторов электромагнитного поля. Рассмотрим эволюцию импульса во времени. Для этого подставим разложение (1) в интеграл (4), который принимает вид

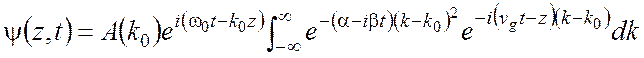              .                                                               (5)

Этот интеграл называется огибающий. Интегрируя с использованием (3), получаем:

                       .

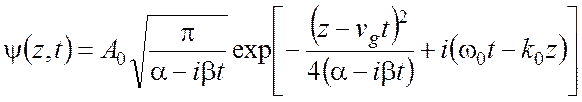Характер зависимости этой комплексной амплитуды (огибающей) от  и  проще исследовать, образовав квадрат модуля, который определяет интенсивность волны:

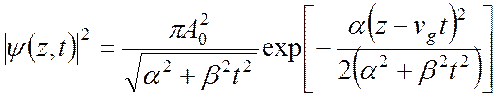                             . (6)

Из этого выражения видно, что интенсивность волны как функция  при фиксированном  имеет вид кривой Гаусса. Полуширина этой кривой  (см. рис. 1), которая определяется из условия, что в точке  величина 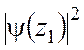 уменьшается вдвое по сравнению с ее максимальным значением при , растет со временем:

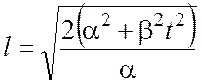                                                  ,                      (7)

а высота убывает за счет множителя . То есть, одномерный волновой пакет расплывается в диспергирующей среде.

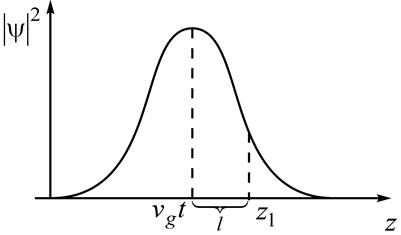
Рис. 3.

Расплывание происходит симметричным образом (в сторону  и в сторону ) и не связано с поглощением энергии, так как  вещественно. Отсутствие диссипации видно и из того, что интеграл

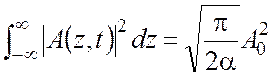                                                               (8)

не зависит от времени, то есть, «полная интенсивность» сохраняется. Причиной расплывания является неодинаковость фазовых скоростей распространения  отдельных плоских волн, входящих в суперпозицию: вследствие дисперсии отношение  зависит от .

Задача 1.2.14

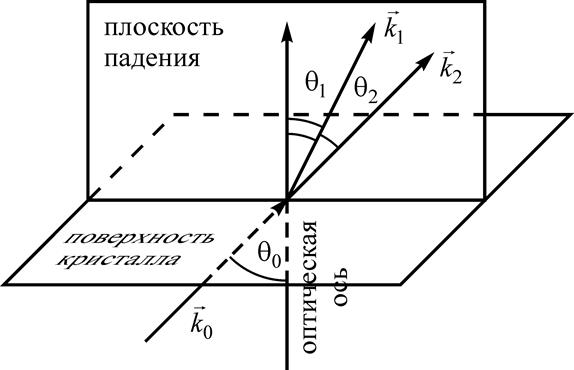
Плоская волна падает из вакуума на плоскую поверхность одноосного кристалла. Оптическая ось кристалла нормальна к его поверхности. Найти направления обыкновенного и необыкновенного лучей в кристалле, если угол падения .

Решение

Отличие от изотропного вещества при отражении и преломлении электромагнитных волн на граничной поверхности среды состоит прежде всего в том, что в анизотропной среде возникают две преломленные волны с различными волновыми векторами (рис.). В одноосных кристаллах одна из главных осей тензора диэлектрической проницаемости  совпадает с осью симметрии кристалла – оптической осью; направления других главных осей произвольны.

Рассмотрим преломление света на поверхности одноосного кристалла, в котором оптическая ось направлена по , тогда в главных осях , .

Направления распространения преломленных волн в кристалле находятся из условий непрерывности поля на границе раздела. Условия непрерывности выполняются только в том случае, если компоненты волновых векторов, параллельные границе раздела, у падающей, отраженной и преломленной волн равны. Волновые векторы преломленных и отраженных волн должны лежать в плоскости падения.

Из граничных условий следует

                                 , .      (1)

Здесь ,  – волновой вектор и угол падения, ,  – волновой вектор и угол преломления обыкновенной волны, ,  – волновой вектор и угол преломления необыкновенной волны (рис.). Из первого соотношения (1) получаем

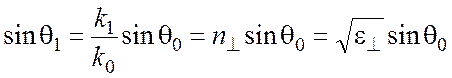                                .    (2)

Для необыкновенной волны

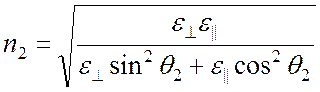                         , где                                                               (2)

получаем

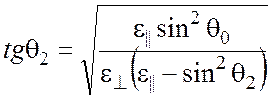                                             .                 (3)

Таким образом, формулы (2) и (3) определяют направления соответственно обыкновенного и необыкновенного лучей в кристалле.

Задача 1.2.15

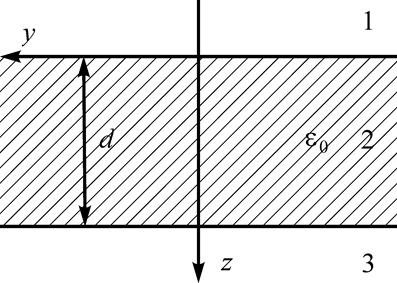
Электромагнитная волна падает нормально на плоскопараллельную пластину, толщина которой – , диэлектрическая проницаемость – . Вне пластины вакуум.

Определить амплитуды электромагнитных волн, отраженной от пластины и прошедшей через нее. Найти условия, при которых отражение волн от пластины минимально.

Решение

Направим ось  перпендикулярно пластине по направлению распространения падающей волны и поместим начало отсчета  на входной границе пластины (см. рис.)

Напряженность электрического поля в однородной изотропной среде находится из волнового уравнения

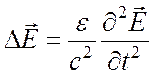                                                     ,                          (1)

где 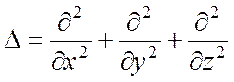 – оператор Лапласа.

Положим, что решение (1) имеет вид

                                                  .                      (2)

Тогда, подставляя (2) в (1), с учетом, что  параллельно оси , получаем

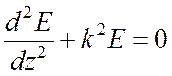                                                    ,                        (3)

где ,  – внутри пластины и  – вне пластины.

Решение (3) вне пластины со стороны падающей волны ищем как суперпозицию падающей и отраженной волн:

                                                ,                    (4)

где  – амплитуда падающей волны,  – отраженной.

Внутри пластины

                                              ,                   (5)

за пластиной – только прошедшая волна с амплитудой

                                                       .                           (6)

Граничные условия (непрерывность тангенциальных составляющих напряженностей электрического и магнитного полей) дают следующую систему уравнений для определения напряженности поля:

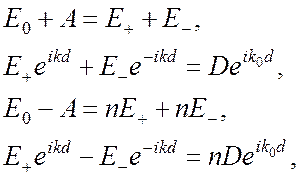                                                           (7)

где  – показатель преломления пластины. Решая эту систему уравнений, находим

                                               ,

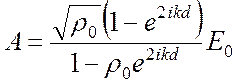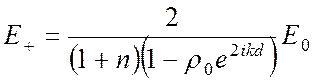                                          ,              (8)

                                         ,

                                                 ,

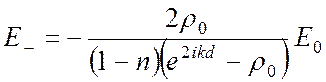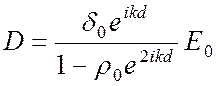где 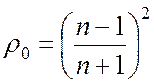,  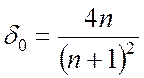– соответственно коэффициенты отражения и прохождения для полубесконечной среды.