Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 15

Особенностью диэлектрической проницаемости холестерического жидкого кристалла (ХЖК) является ее зависимость от координат. Это означает, что ХЖК является не только анизотропным, но и неоднородным веществом. Поэтому проведенное в лекции 4 рассмотрение прохождения света в анизотропных, но однородных средах не может быть здесь использовано.

Заметим, что из определения директора следует, что

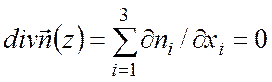                                             , ,                            (1)

откуда вытекает, что

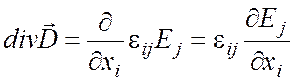                                           ,                (2)

здесь и в дальнейшем по дважды встречающемуся индексу подразумевается суммирование. Уравнение , с учетом (2), приобретает вид

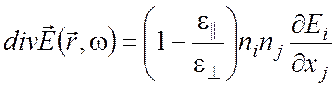                                        .             (3)

Из уравнений Максвелла следует уравнение (см. лекцию 1)

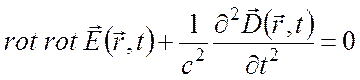                                       ,           (4)

которое, учитывая (3), преобразуем к виду

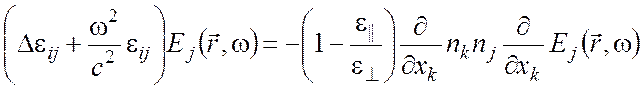              .                                                               (5)

Рассматриваем случай, когда волна распространяется вдоль оси спирали холестерика (см. рис. 1), т.е. вдоль оси . В этом случае поле зависит только от координаты  и в (3) отлична от нуля только производная по , но для нее , поэтому  и правая часть (5) исчезает. Это означает, что поле – чисто поперечное, и отличаются от нуля только компоненты  и .

Рис. 1. Схематическое представление расположения молекул в холестерике.

Подставляя явный вид  в (5), можно для поля, распространяющегося вдоль оси  получить уравнения

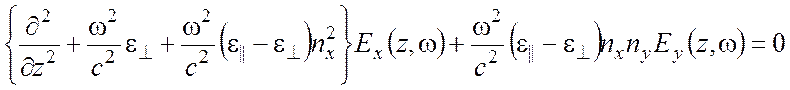,                                                              (6)

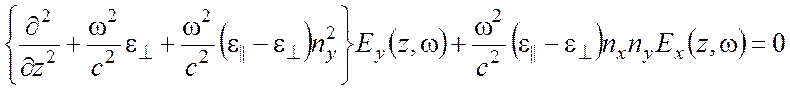.                                                              (7)

Вводя переменные

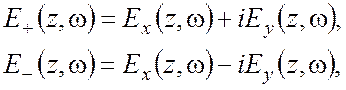                                                     (8)

так что

                                    

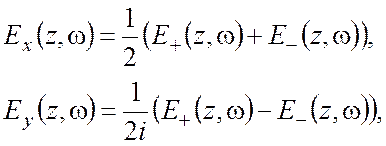
преобразуем (6), (7) к виду

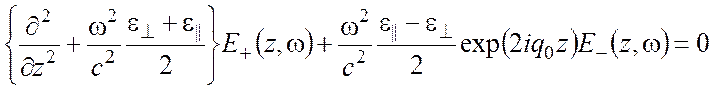    ,                                                               (9)

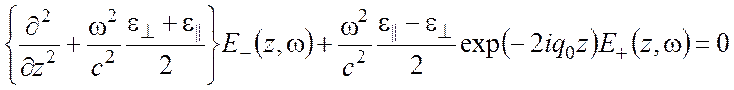.                                                              (10)

Вводя обозначения 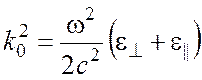,  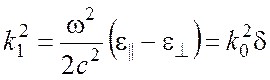и полагая

                                       ,         (11)

можно привести систему уравнений (9), (10) к форме

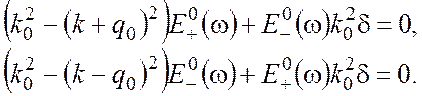                                        (12)

Получилась система двух однородных алгебраических уравнений относительно амплитуд  и . Как известно, условием существования нетривиальных решений такой системы является обращение в нуль ее определителя

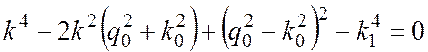                                  .    (13)

Для данной частоты  волновые векторы  и  фиксированы, уравнение (13) дает четыре возможных значения  (действительных или комплексных). Соотношение между  и  для действительных  называется дисперсионным соотношением. Оно показано на рис. 2, который следует из анализа решений уравнения (13). Имеются две различные ветви, которые мы назовем (+) и (–). Чтобы найти их, удобно рассмотреть сначала случай . Это дает

                                                     .

Возвращаясь к определению  и , получаем следующие частоты

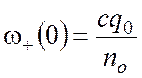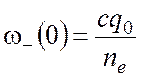                                          , ,            (14)

где ,  – соответственно обыкновенный и необыкновенный показатели преломления.

Заметим, что оптическая ось холестерика определяется лишь локально и параллельна осям молекул (или директору). При малых  в (13) можно отбросить слагаемое  тогда

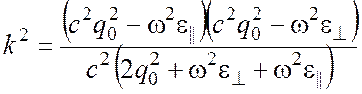                                       .         (15)

Отсюда видно, что при малых  нет действительных корней уравнения, если частота  находится между значениями  и . Эта область называется частотной щелью, или иначе запрещенной зоной фотонного кристалла, каковым является холестерический жидкий кристалл (см. рис. 2). В силу того, что пространственный период спирали директора имеет величину около 3000 Å возможно брэгговское отражение от холестерика в видимом спектральном диапазоне.

При малых частотах

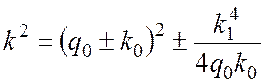                                             ,                (16)

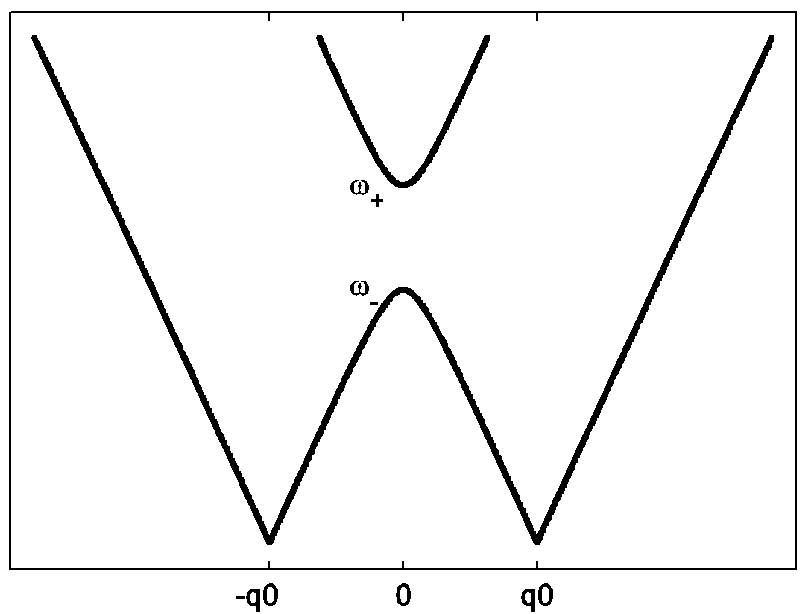
Рис. 2. Соотношение между частотой и волновым вектором  для распространения электромагнитных мод в спирали холестерика.

так что при нулевой частоте .

Заметим, что ветвь , соответствующая знаку плюс в уравнении

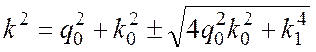                                          ,            (17)

которое следует из (13), дает монотонный рост  с квадратом частоты. Это означает, что такая кривая может только один раз пересечь ось частот (). С другой стороны, это пересечение должно находиться в верхней точке частотной щели, чтобы в щели не было действительных решений при малых . Остальные пересечения кривой  с осью частот в нижней точке частотной щели и пересечение с осью  в точках  относятся ко второй ветви  (). Эта ветвь изменяется с частотой не монотонно и имеет минимум при ,  и максимум при  в нижней точке частотной щели. Таким образом в частотной щели имеется два действительных корня дисперсионного уравнения, а в остальных областях – четыре действительных корня.

Литература

1.  Ярив А.,Юх П. Оптические волны в кристаллах. М.:Мир, 1987г.

2.  Рязанов М.И. Электродинамика конденсирвоанного вещества. М.: Наука. 1984. 303 с.

3.  Батыгин В.В., Топтыгин И.Н. Сборник задач по электродинамике. М.: Наука, 1970, 503 с.

4.  Сборник задач по теоретичской физике. Учебн. пособие для вузов. М., «Высшая школа», 1972, 336 с.

5.  Шабанов В.Ф., Ветров С.Я., Шабанов А.В. Оптика реальных фотонных кристаллов. Жидкокристаллические дефекты, неоднородности. Новосибирск, Изд-во СО РАН, 2005г.

Содержание

Введение. 3

1. Общий порядок проведения аудиторных занятий. 4

2. План аудиторных занятий. 5

3. Самостоятельная работа студентов. 11

4. Перечень задач для практических занятий. 13

Модуль 1 Распространение электромагнитных волн в веществе. 13

Раздел 1. Основные свойства электромагнитного поля. 13

Раздел 2. Распространение волн  в анизотропных и плоскослоистых средах. 18

Модуль 2. Фотонные кристаллы и их получение. 25

Раздел 3. Электрооптическое управление спектром собственных электромагнитных возбуждений в фотонных кристаллах. 25

Раздел 4. Теория связанных мод и ее применение. 29

Раздел 5. Волноводы на основе фотоннокристаллических структур. 30

Модуль 3 Исследование оптических свойств фотонных кристаллов. 32

Раздел 6. Спектры пропускания фотонных кристаллов с дефектами решетки. 32

Раздел 7. Распростарнение интенсивного лазерного излучения  в фотонно-кристаллических средах. 38

Раздел 8. Фотонный холестерический жидкий кристалл. 40

5. Примеры решения задач. 42

Литература. 74