Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 6

Определить характеристики волны, получаемой в результате суперпозиции двух волн с одинаковой амплитудой, поляризованных по правому и левому кругу, если в начальный момент разность фаз волн равна .

Модуль 2. Фотонные кристаллы и их получение

Раздел 3. Электрооптическое управление спектром собственных электромагнитных возбуждений в фотонных кристаллах

Задача 2.3.1. Линейные электрооптические коэффициенты и симметрия кристалла

Если – матричное представление операции инвариантной симметрии кристалла, то преобразованный электрооптический тензор имеет вид

                                                  .

Этот тензор вследствие симметричности совпадает с исходным тензором, т. е. .

а) Моноклинная группа 2. Пусть z – ось двумерного вращения С₂. Матричное представление С₂ записывается в виде

                                                 .

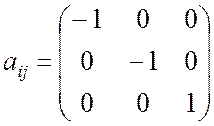Покажите, что

                                             .

Таким образом, электрооптический коэффициент равен нулю, если индексы 1 и 2 возникают один или три раза, – иными словами, если индекс 3 возникает нуль или два раза.

б) Моноклинная группа m. Пусть ху – плоскость зеркальной симметрии а. Матричное представление для а имеет вид

                                                  .

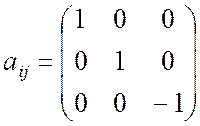Покажите, что, как в пункте а),

                                             .

Таким образом, электрооптический коэффициент равен нулю, если индекс 3 возникает один или три раза. Покажите также, что обращающиеся в нуль элементы электрооптического тензора для точечной группы m являются дополнительными к элементам для точечной группы 2, если двумерная ось в случае группы 2 перпендикулярна плоскости зеркальной симметрии в случае группы m.

в) Орторомбическая группа 222. Точечная группа 222 имеет три взаимно перпендикулярные двумерные оси х, у и z. Покажите с помощью результата, полученного в п. а задачи, что единственные отличные от нуля компоненты электрооптического тензора равны r₁₂₃, r ₂₃₁ и r ₃₁₂.

г) Тетрагональная группа  (кристаллы типа KDP – ADP). Точечная группа  имеет симметрию группы 222, а также двумерную вращательно-инверсионную симметрию 2S₄ и две зеркальные симметрии. Вращательно-инверсионная симметрия представляет собой поворот на  вокруг оси z с последующей инверсией относительно начала координат. Покажите, что матричное представление оператора этой симметрии имеет вид

                                                 .

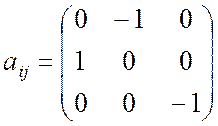Покажите, что . Из этого следует, что для кристаллов группы  мы имеем .

д) Кубическая группа . Точечная группа  имеет все симметрии группы , а также трехмерные вращения и другие симметрии. Простейшей операцией трехмерного вращения является , и , что можно записать в виде матрицы

                                                   .

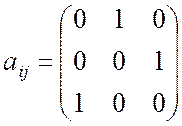Покажите, что , откуда следует .

Задача 2.3.2. Электрооптический эффект в одноосных кристаллах

Рассмотрим случай, когда электрическое поле приложено вдоль оси  (c-оси) электрооптического одноосного кристалла. В кристаллах группы  новый эллипсоид показателей преломления имеет вид

                         .

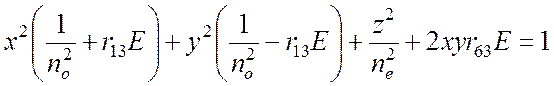а) Покажите, что новые главные оси получаются вращением прежних главных осей на угол  вокруг оси . Этот угол не зависит от напряженности электрического поля  и дается выражением

                                                     .

б) Покажите, что главные значения показателя преломления записываются в виде

                                     

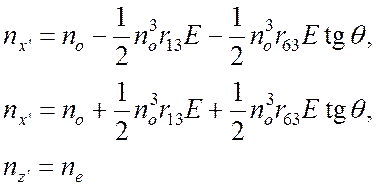
в) Покажите, что для светового пучка, распространяющегося вдоль оси , двулучепреломление равно

                                             .

Задача 2.3.3.

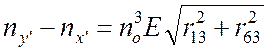Придумайте физическую модель, объясняющую разрушение одноосной симметрии, даже если электрическое поле действует вдоль оси симметрии.

Задача 2.3.4. Электрооптическая перестраиваемая фазовая пластинка (продольная)

Пусть имеется волновая пластинка, изготовленная из электрооптического кристалла толщиной d. Если поперек пластинки приложено напряжение V, то фазовая задержка Г оказывается пропорциональной приложенному напряжению, т. е. ее можно перестраивать с помощью электрического поля. Покажите, что фазовые задержки для разных пластинок определяются представленными ниже выражениями

а) для -среда пластинки группы :

                                                     .

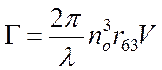б) для -среда пластинки группы : .

                                               .

Задача 2.3.5.

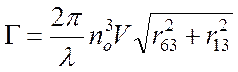Получите уравнения Максвелла (8.4) для опсания волн распространяющихся в анизотропной среде сверхрешенки, в качестве которой рассматривается слой нематического жидкого кристалла.

Задача 2.3.6.

Выведите дисперсионное уравнение для объемных электромагнитных волн в одномерном фотонном кристалле (выражение (8.23) лекций).

Задача 2.3.7.

Выведите дисперсионное уравнение для поверхностных электромагнитных волн (ПЭВ), распространяющихся вдоль границы раздела изотропной среды и сверхрешетки (выражение (8.28) лекций).

Задача 2.3.8.

Используя дисперсионное соотношение (8.28), получите закон дисперсии ПЭВ, распространяющихся вдоль границы раздела изотропных; изотропной и анизотропной сред (выражения (8.32), (8.30) лекций, соответственно).

Раздел 4. Теория связанных мод и ее применение

Задача 2.4.1. Сохранение энергии мод

Покажите, что уравнения связи одинаково направленных волн (9.28) согласуются с условием сохранения энергии (9.29).

Задача 2.4.2

Получите общее решение [выражения (9.30) и (9.31)] системы уравнений связанных мод (9.28) и покажите, что оно подчиняется условию сохранения энергии (9.29).

Задача 2.4.3

Покажите, что уравнения связи противоположно направленных волн (9.34) и (9.35) согласуются с условием сохранения энергии (9.36).

Задача 2.4.4

Получите общее решение [выражения (9.37) и (9.38)] и покажите, что оно согласуется с (9.36).

Задача 2.4.5. Брэгговские отражатели

Выведите выражения для постоянных связи как для ТЕ-, так и для ТМ-волн [выражения (10.6)].

Задача 2.4.6

Покажите, что ширина полосы брэгговского отражателя не зависит от длины структуры L.

Задача 2.4.7

в) Покажите, что коэффициент отражения при s = 0 конечен (т. е. ).

Задача 2.4.8

г) Покажите, что первый нуль коэффициента отражения имеет место при . Чему равна величина  в этой точке?