Вместо гладкой зависимости на рис. 2 вы видите 501 расчетную точку, которые соединены между собой 500 отрезками. Заметно, что этого количества недостаточно, чтобы прописать изменения в запрещенной зоне, вызванные дефектами. Хотя время расчета уже достигает нескольких секунд. В серединах первой и третьей запрещенных зонах видно по одной точке с ненулевым пропусканием, а во второй зоне даже эту точку практически не видно. По виду все запрещенные зоны одинаковы. Этого следовало ожидать, так как структура настроенная: оптическая толщина слоев совпадает.
Рисунки 3 и 4 дают более четкое представление о том, что происходит в запрещенной зоне. Оба пика имеют широкие основания и напоминают лоренцевы контура. Максимальные пропускания в пиках достигают 1. Этого также следовало ожидать, так как в среде не было учтено затухание: показатели преломления чисто действительные. Если прописать пики еще подробнее, то станет заметно, что вержины пиков не острые, а закругленные.
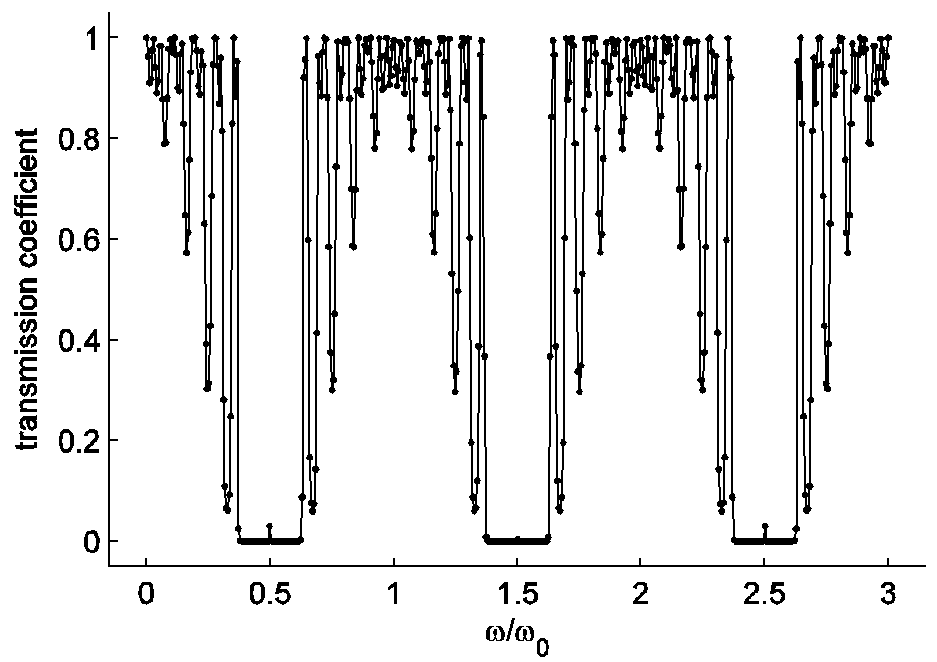
Рис. 2. Частотная зависимость коэффициента пропускания. 
измеряется в единицах 
, где 
–
оптическая толщина.
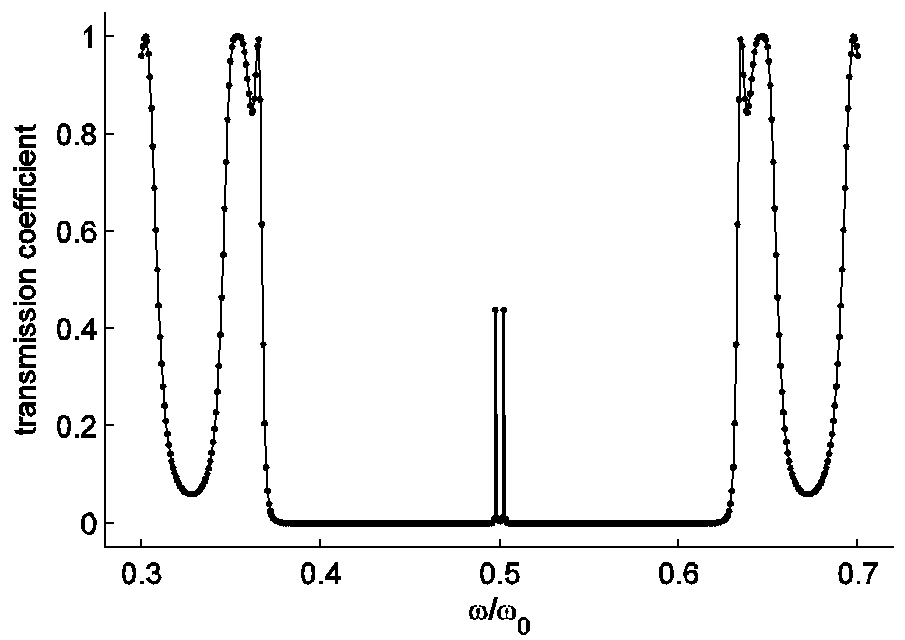
Рис. 3. Первая запрещенная зона в частотной зависимости коэффициента пропускания.
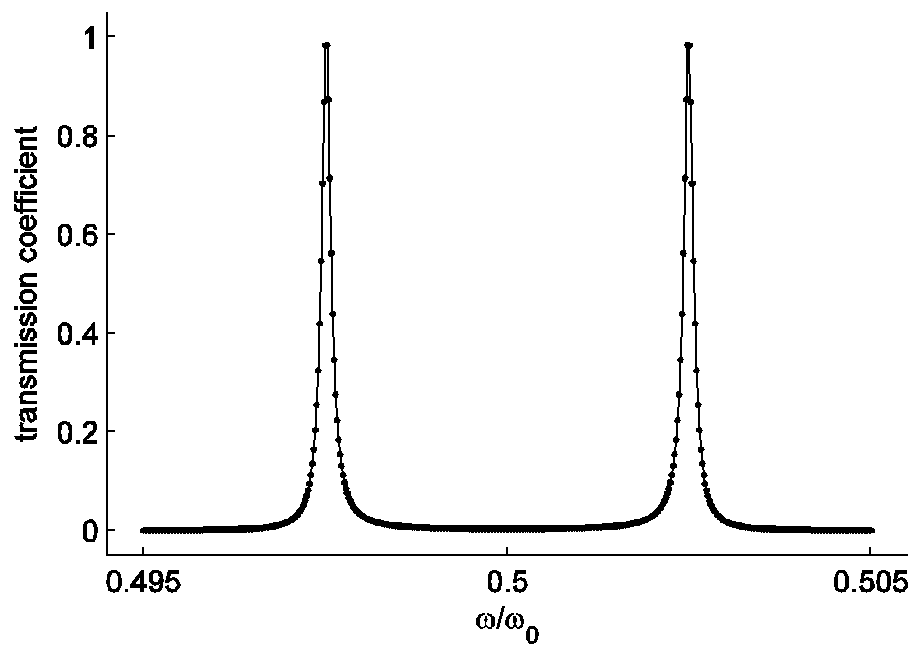
Рис. 4. Пики пропускания в запрещенной зоне, соответствующие дефектным модам.
б) Найти распределение интенсивности поля в фотоном кристалле для частот дефектных мод.
Примем, что частоты дефектных мод
,
где 
.
На рисунке 5 изображено распределение поля в среде для
частоты 
. Интенсивность нормирована на свое
максимальное значение. Изменив знак при 
,
легко убедиться, что на частоте 
программа выдает
в точности такое же распределение интенсивности. С одной стороны, понятно, что
длины волн на дефектных частотах отличаются на 1/200. И поэтому картины
выглядят одинаково. С другой стороны, непонятно почему поле локализовано сразу
в двух дефектах. То есть, нет однозначного соответствия между двумя модами и
двумя дефектами. Чем же вообще отличаются две рассматриваемые моды?
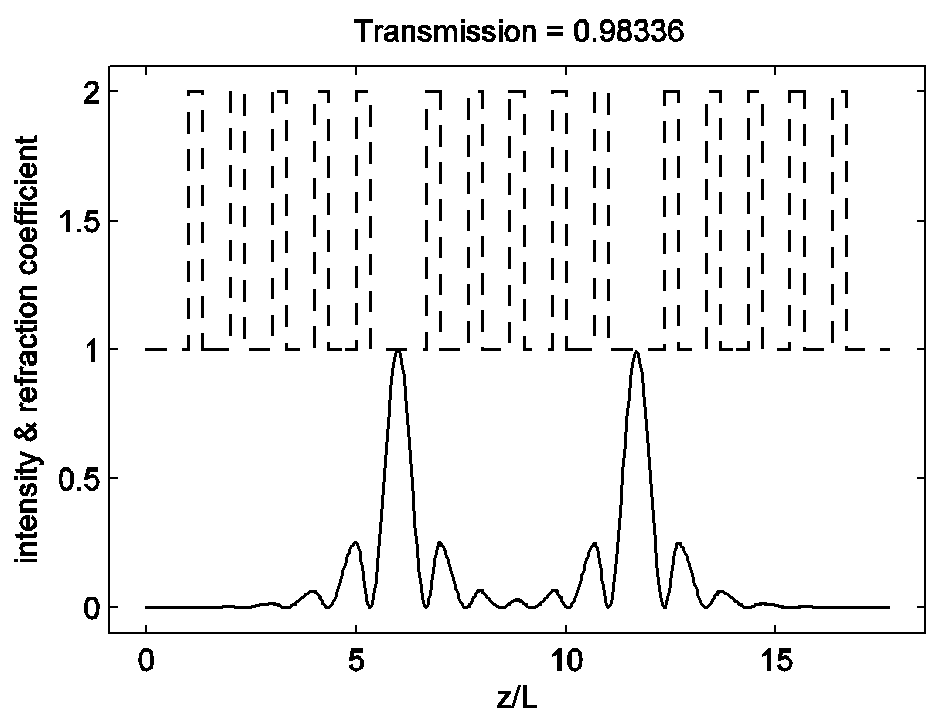
Рис. 5. Показатель преломления слоев среди и распределение интенсивности
поля в среде на частоте дефектной моды .
Глубина среды 
измерена в периодах ФК 
.
Ответ дают рис. 6 и рис. 7. Здесь вместо интенсивности изображена действительная часть напряженности электрического поля для каждой из мод.
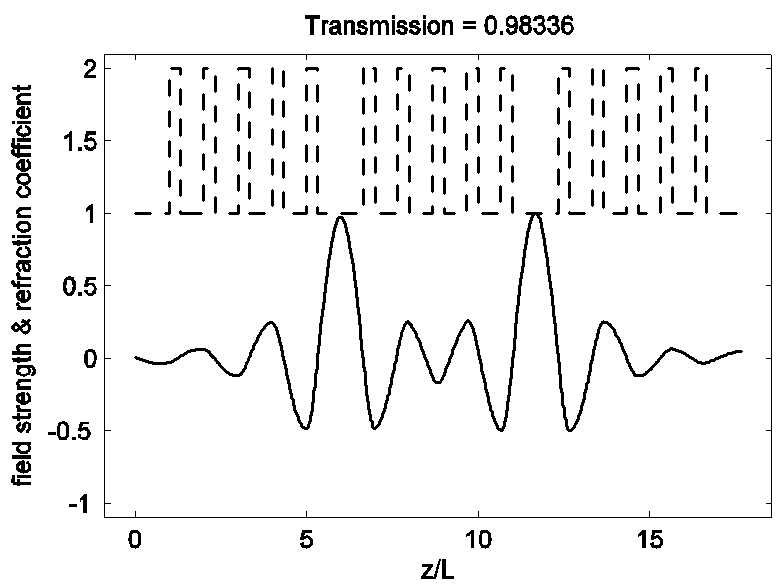
Рис. 6. Распределение напряженности поля в среде на частоте дефектной
моды .
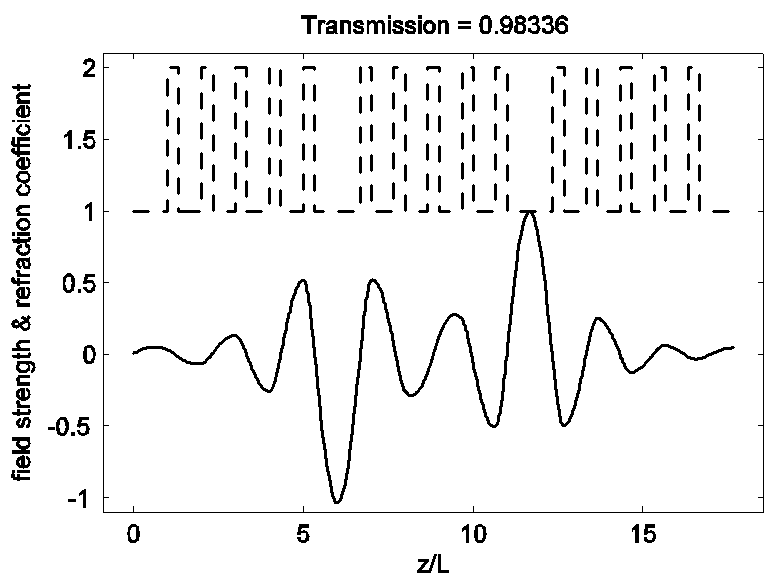
Рис. 7. Распределение напряженности поля в среде на частоте дефектной
моды 
.
в) Дефектные слои представляют собой одинаковые микрорезонаторы, однако частоты в запрещенной зоне, соответствующие их резонансам разошлись, произошло снятие вырождения. Объясните его механизм. Сопоставьте данное явление с изменением частоты нормальных колебаний при взаимодействии двух одинаковых математических маятников, подвешенных на одну провисающую нить.
Механизм снятия выраждения явствует из аналогии рисунков 6 и 7 с колебаниями двух одинаковых маятников на провисающей горизонтальной нити, когда маятники колеблятся перпендикулярно нити в одном направлении, или в противоположных направлениях. То есть, когда фаза маятников одинакова и когда она противоположна. Если маятники колеблятся в противоположной фазе, то провисающая нить-подвес практически не смещается. Когда же маятники раскачиваются в фазе, то вместе с маятниками раскачивается и нить-подвес, тем самым увеличивая длину маятников и уменьшая частоту колебаний.
г) Как изменятся пики пропускания, если дефекты переместили в третий и двенадцатый воздушные зазоры.
Как видно из рис. 8 и, особенно, рис. 9, вырождение дефектных мод снято. Это обусловлено тем, что расстояние между дефектами увеличилось и связь ослабла. Еще более явственно заметно, что пропускание в пике значительно упало, а сам пик уширился. Это объясняется тем, что упала добротность дефектных контуров, так как каждый из них оказался близок к границе ФК и поле, локализованное в дефекте, быстро уходит.
Сначала следует скопировать программу их этого текста через буфер обмена. В случае, если в наличие имеется только бумажная копия, программу можно сосканировать и распознать. Номера строк – удалить через автозамену.
Запуск программы приведет к построению рис. 2.
Чтобы воспроизвести графики рис. 3 и 4, следует заменить строчку №8 исходной программы с
Nx = 501; Rx = [0 3]; .5+.005*[-1 1];
на
Nx = 501; Rx = .5+.2*[-1 1]; [0 3];
или
Nx = 501; Rx = .5+.005*[-1 1]; [0 3];
Рис. 5 получается после замены строки №5 с
xName = 'Friq'; % Friq Wave Angle Space
на
xName = 'Space'; % Friq Wave Angle Space
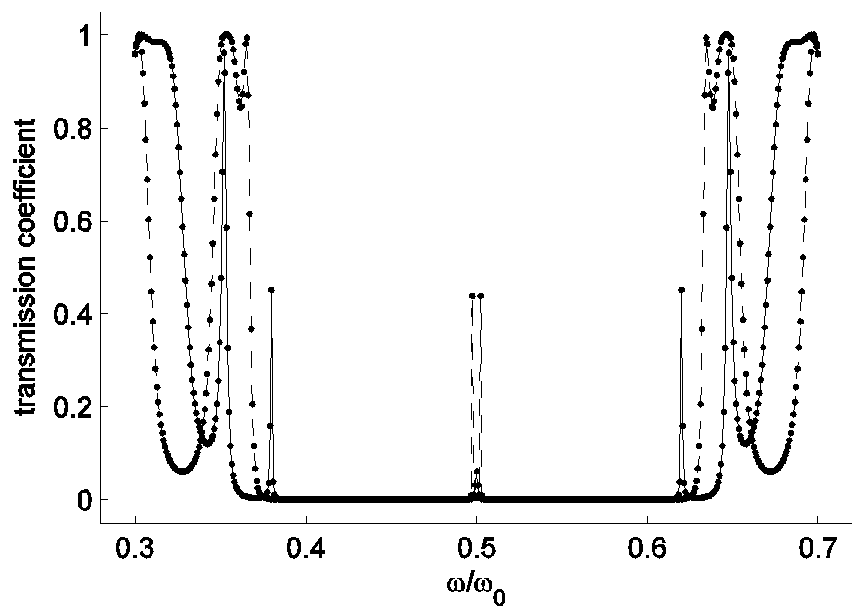
Рис. 8. Пунктиром воспроизведен спектр рис. 3. Сплошной линией обозначен спектр в случае, когда дефекты смещены на края, в 3 и 12 воздушные зазоры.
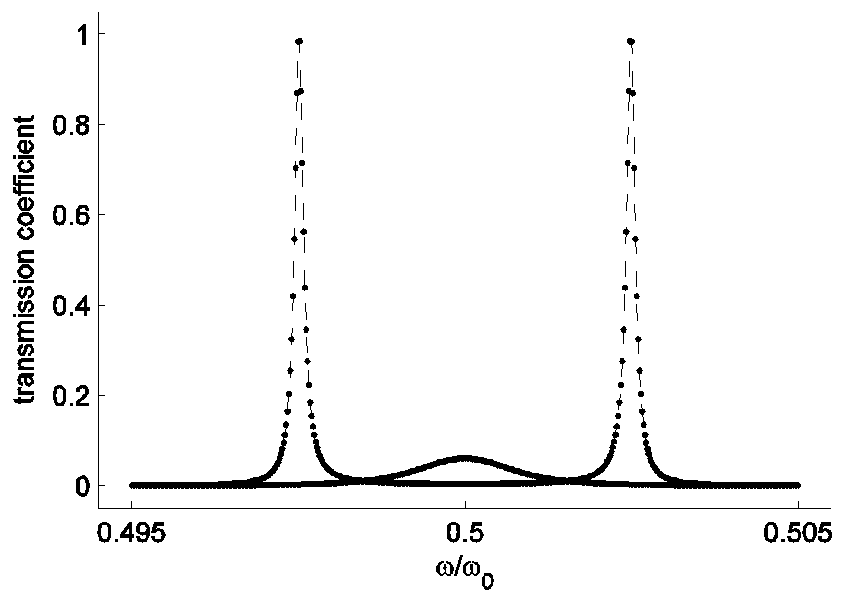
Рис. 9. Пунктиром воспроизведен спектр рис. 4. Сплошной линией обозначен спектр в случае, когда дефекты смещены на края, в 3 и 12 воздушные зазоры.
Рис. 6 получается после снятия комментария со строк №№108,109:
% Intensity = real(sum(E));
% axis ([max(zg)*[-.05 1.05] 2*[-.55 1.05]])
заменяется на
Intensity = real(sum(E));
axis ([max(zg)*[-.05 1.05] 2*[-.55 1.05]])
Рис. 7 получается из рис. 6 заменой знака в строке №12:
Rx = .5+.0025; Nx = 1; Rx = [Rx Rx];
заменяется на
Rx = .5-.0025; Nx = 1; Rx = [Rx Rx];
Рис. 8 и 9 получаются из так же, как и рисунки 3 и 4, с дополнительным снятием комментария строк №№34-36:
% latt = [1,repmat([2,3],1,2),2,4,...
% repmat([2,3],1,8),2,4,...
% repmat([2,3],1,2),2,1];
заменяются на
latt = [1,repmat([2,3],1,2),2,4,...
repmat([2,3],1,8),2,4,...
repmat([2,3],1,2),2,1];
Тензор диэлектрической проницаемости 
холестерического
жидкого кристалла (или холестерика) определяется формулой
.
где 
, 
– диэлектрические проницаемости для
электрического поля соответственно параллельного и нормального единичному
вектору (
, называемому директором), который
задает ориентацию молекул изменяющуюся с изменением по
спирали:
,
, 
.
Пространственный период спирали директора 
.
Определить связь между частотой и волновым вектором электромагнитной волны распространяющейся вдоль оси спирали холестерика.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.