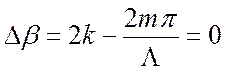 ,
,
которое можно также записать в виде ![]() .
Физически это означает, что пространственные гармоники
.
Физически это означает, что пространственные гармоники ![]() и
и ![]() резонансно
связаны.
резонансно
связаны.
б) Предполагая, что свет падает теперь под углом ![]() , покажите, что условие Брэгга
, покажите, что условие Брэгга ![]() согласуется с выражением (5.8)
лекций.
согласуется с выражением (5.8)
лекций.
в) Пусть ![]() – центр запрещенной зоны;
покажите, что
– центр запрещенной зоны;
покажите, что
![]() ,
,
где ![]() .
.
г) Пусть ![]() – мнимая часть
волнового числа в запрещенной зоне, так что
– мнимая часть
волнового числа в запрещенной зоне, так что
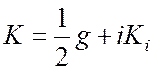 .
.
Покажите, что связь между ![]() и
и
![]() дается выражением
дается выражением
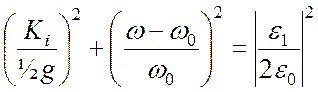
Заметьте, что это выражение описывает эллипсоид с центром ![]() и
и ![]() .
.
д) С помощью выражений, приведенных в пункте г), покажите, что ширина запрещенной зоны дается выражением
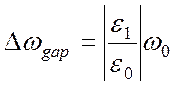 ,
,
а максимальное значение ![]() равно
равно
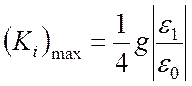 .
.
Среда, в которой пространственный период изменения диэлектрической проницаемости (показателя преломления) равен половине полного периода, называется полуволновой средой. Иными словами, профиль показателя преломления такой среды дается выражением
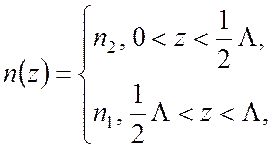
причем
![]() .
.
а) Пусть ![]() определена следующим образом:
определена следующим образом:
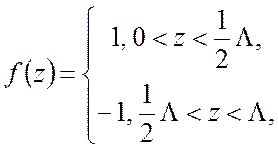
причем ![]() . Покажите, что
. Покажите, что
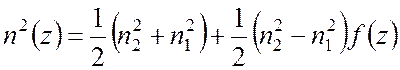
б) Покажите, что Фурье-разложение функции ![]() имеет
вид
имеет
вид
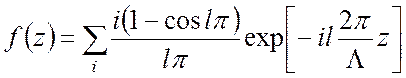 .
.
в) Покажите, что ширина первой запрещенной зоны (l = 1) для этой среды дается выражением
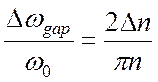 .
.
Получите выражения (6.12) для матричных элементов А, В, С, D.
Получите выражения (6.14).
Выведите уравнение на собственные значения (6.21) лекций.
Найдите решения (6.22)-(6.24) уравнения на собственные значения (6.21) лекций.
Получите явные выражения для cos К А, используя матричные элементы (6.12) и (6.14) для ТЕ- и ТМ-волн и дисперсионное уравнение (6.24) лекций.
Покажите, что в случае нормального падения (kv = 0) выражения, полученные в п. в, сводятся к (6.26).
Покажите, что для волны, падающей на поверхность кристалла под углом
Брюстера [![]() ], блоховское волновое число всегда вещественное.
[Указание: В = С = 0, AD =
1.]
], блоховское волновое число всегда вещественное.
[Указание: В = С = 0, AD =
1.]
Пусть имеется периодическая слоистая структура, состоящая из двух чередующихся диэлектрических сред, профиль показателя преломления которой определяется выражением (6.1) лекций.
а) Используя выражения, полученные в задаче 1.2.7, покажите, что максимум величины ![]() достигается
при
достигается
при
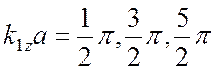 ,…
,…
и
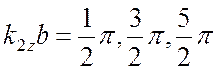 ,…
,…
Слоистая структура, удовлетворяющая этим условиям, называется четвертьволновым массивом.
б) Получите выражения для максимальных значений cos KL как для ТЕ-, так и для ТМ-волн.
в) Покажите, что при нормальном падении эти выражения сводятся к (6.29).
г) Покажите, что амплитуда затухающей блоховской волны при нормальном
падении на четвертьволновый массив уменьшается в п2/п]
раз на каждом периоде (положите ![]() ).
).
Коэффициент пропускания брэгговского отражателя определяется выражением
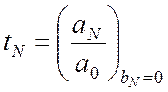 .
.
а) Покажите, что
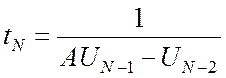 .
.
б) Коэффициент пропускания энергии световой волны Т дается выражением
![]() .
.
Покажите, что
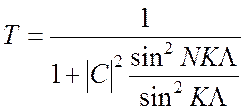 .
.
Заметьте, что ![]() и
и ![]() .
.
в) Выведите формулу (6.42) лекций, используя соотношение R = 1 – Т.
Формулы для коэффициента отражения (6.42) и для коэффициента пропускания,
приведенные в задаче 1.2.11, справедливы, только если свет падает из среды с
показателем преломления ![]() . Покажите,
что если свет падает из среды с показателем
преломления па (для воздуха па = 1), то
коэффициент отражения записывается в виде
. Покажите,
что если свет падает из среды с показателем
преломления па (для воздуха па = 1), то
коэффициент отражения записывается в виде
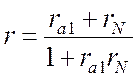 ,
,
где ![]() определяется выражением (6.41) лекций, а
определяется выражением (6.41) лекций, а ![]() –
коэффициент отражения света, падающего из среды с показателем преломления па
на среду с показателем преломления n1Для случая нормального падения
–
коэффициент отражения света, падающего из среды с показателем преломления па
на среду с показателем преломления n1Для случая нормального падения
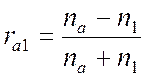 .
.
[Указание: используйте формулу Эйри, предполагая, что бесконечно тонкий слой с показателем преломления ![]() расположен между средой с показателем преломления па
и брэгговским отражателем. Формулы Эйри для коэффициентов отражения
и пропускания записываются в виде
расположен между средой с показателем преломления па
и брэгговским отражателем. Формулы Эйри для коэффициентов отражения
и пропускания записываются в виде
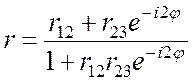 ,
, 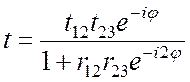 ,
,
где
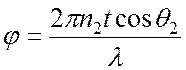 .
.
Плоская волна падает из вакуума на плоскую поверхность одноосного
кристалла. Угол падения ![]() . Оптическая ось
кристалла параллельна его поверхности и составляет угол
. Оптическая ось
кристалла параллельна его поверхности и составляет угол ![]() с
плоскостью падения. Найти направление обыкновенного и необыкновенного лучей в кристалле
(см. лекцию).
с
плоскостью падения. Найти направление обыкновенного и необыкновенного лучей в кристалле
(см. лекцию).
Плоская волна падает из вакуума на плоскую поверхность одноосного
кристалла. Оптическая ось кристалла нормальна к его поверхности. Найти
направления обыкновенного и необыкновенного лучей в кристалле, если угол
падения ![]() .
.
Электромагнитная волна падает нормально на плоскопараллельную
пластину, толщина которой – ![]() , диэлектрическая
проницаемость –
, диэлектрическая
проницаемость – ![]() . Вне пластины вакуум.
. Вне пластины вакуум.
Определить амплитуды электромагнитных волн, отраженной от пластины и прошедшей через нее. Найти условия, при которых отражение волн от пластины минимально.
Плоская волна с амплитудой электрической напряженности ![]() , распространяясь в воздухе с коэффициентом
преломления
, распространяясь в воздухе с коэффициентом
преломления ![]() , падает под прямым углом на плоскую
границу полупроводника с коэффициентом преломления
, падает под прямым углом на плоскую
границу полупроводника с коэффициентом преломления ![]() .
Используя непрерывность поля на границе, рассчитайте и изобразите векторы
напряженности электрического и магнитного полей для падающей, отраженной и прошедшей
волн.
.
Используя непрерывность поля на границе, рассчитайте и изобразите векторы
напряженности электрического и магнитного полей для падающей, отраженной и прошедшей
волн.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.