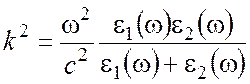Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 12

                                               .                 (14)

Сравнивая это равенство с условием (9), можно заключить, что рассматриваемое нами решение возможно не только при условии , но должно выполняться условие

                                                   .                     (15)

Дисперсионное соотношение (14) можно записать иначе, вводя показатель преломления  для поверхностной электромагнитной волны

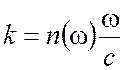                                                        ,                          (15)

где

                                                   .

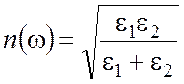Подстановка (8) в (12), (13) дает выражения для волновых векторов, нормальных к поверхности раздела

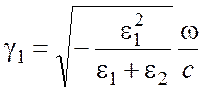                                                  ,                    (16)

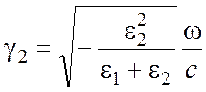                                                  .                    (17)

Используя (15), запишем выражения (16), (17) в виде

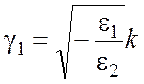                                                      ,                        (18)

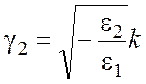                                                      .                        (19)

Для определения характера поляризации поверхностной волны найдем компоненты вектора электрического поля. Из уравнения

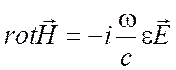                                                                           (20)

следует, что, в соответствии с (20) и (8)

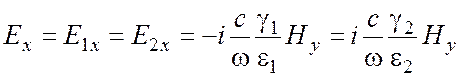                               ,  (21)

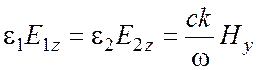                                              .                (22)

Подстановкой в (21), (22) выражений (19), (15) соответственно для  и  окончательно найдем компоненты вектора электрического поля, комплексные амплитуды которых на границе раздела равны

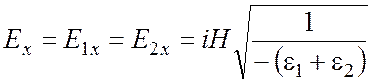                                      ,        (23)

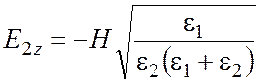                                              ,                (24)

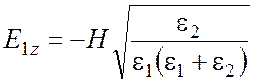                                              .                 (25)

Для выполнения условий (8), (15) полагаем , . Из выражений (23)-(25) видно, что в отличие от объемных, чисто поперечных электромагнитных волн, поверхностные электромагнитные волны являются частично поперечными и частично продольными волнами. Электрический вектор волны  имеет две составляющие: компоненту, расположенную в плоскости раздела и направленную вдоль волнового вектора волны  и компоненту, перпендикулярную плоскости раздела. Вектор магнитного поля перпендикулярен направлению распространения волны и расположен в плоскости раздела. В результате наличия продольной компоненты электрического поля , поток энергии, который пропорционален , циркулирует через поверхность раздела из одной среды в другую.

Из выражений (23)-(25) видно, что  сдвинут по фазе относительно поля вектора  на , а  на . Действительно,

                                        , ;

  , , .

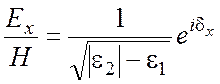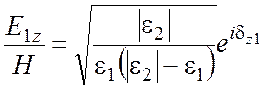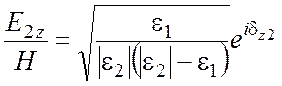Из выражений (23)-(25) следует также, что

                                                   .

Следовательно, если зафиксировать координату , вектор  в обеих средах вращается по часовой стрелке, описывая эллипсы, как показано на рис. 1, б. В среде с положительной  описываемая вектором траектория вытянутая, а в среде с отрицательной  – сплюснутая.

Наконец, рассмотрим в качестве примера поверхность раздела металл-вакуум, когда можно считать

                                        , ,          (26)

где  есть частота собственных колебаний электронной системы металла (плазменная частота). Величина плазменной частоты для металлов может составлять порядка  Гц. Закон дисперсии (14) для поверхностных волн на границе металл-вакуум с диэлектрическими проницаемостями сред (26) приобретает вид

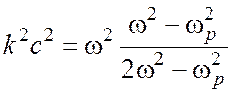                                                .                  (27)

Зависимость частоты  от  определится уравнением

                                  ,

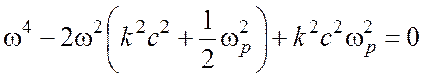решение которого имеет вид

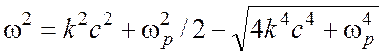                                     .       (28)

Решение со знаком «+» перед корнем отброшено из-за того, что для него не выполняется условие . При малых  () можно написать

                                                      .                        (29)

В обратном случае

                                                     .                       (30)

Заметим, что в этом предельном случае частота поверхностной волны в  раз меньше частоты объемной продольной волны, удовлетворяющей условию , т.е. . Это позволяет отличать поверхностные волны от объемных продольных волн.

Задача 3.6.15 Вырождение и расщепление частот дефектных мод

Одномерный фотонный кристалл состоит из 15 периодов. Пятнадцать одинаковых плоских алмазных пластинок с коэффициентом преломления  толщиной  каждая, расположенных параллельно друг другу с воздушными зазорами с показателем преломления  толщиной  каждый. В такой фотонный кристалл внедили два дефекта, увеличив пятый и десятый воздушные зазоры вдвое (см. рис. 1).

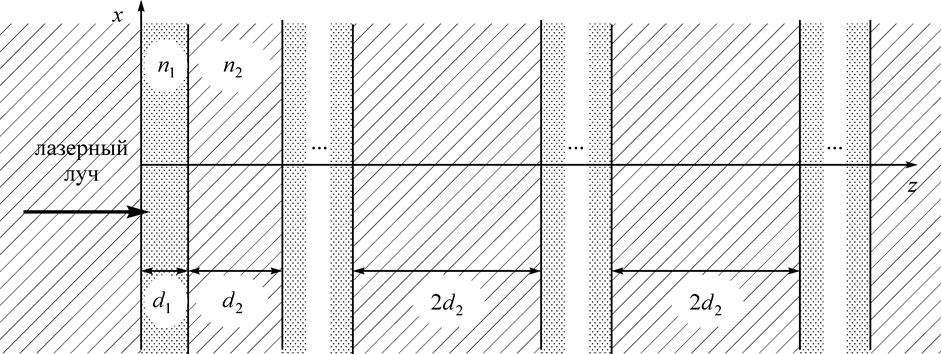
Рис. 1. Конечный фотонный кристалл с двумя дефектами.

а) Методом трансфер-матрицы провести расчет спектра пропускания фотонного кристалла в случае нормального падения света на образец.

б) Найти распределение интенсивности поля в фотоном кристалле для частот дефектных мод.

в) Дефектные слои представляют собой одинаковые микрорезонаторы, однако частоты в запрещенной зоне, соответствующие их резонансам разошлись, произошло снятие вырождения. Объясните его механизм. Сопоставьте данное явление с изменением частоты нормальных колебаний при взаимодействии двух одинаковых математических маятников, подвешенных на одну провисающую нить.

г) Как изменятся пики пропускания, если дефекты переместили в третий и двенадцатый воздушные зазоры.

Алгоритм

Коэффициент пропускания  одномерного фотонного кристалла определяется в лекциях формулой (13.28):

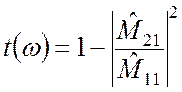                                                   ,                        (1)

где ,  – элементы матрицы  (13.26), которая связывает амплитуды падающей на кристалл  и отраженной от него  волн, с амплитудой прошедшей волны . Связь между амплитудами полей в соседних слоях фотонного кристалла устанавливает матричное уравнение (13.21).

Ниже приведена программа, которая позволяет расчитать спектр пропускания  и распределение интенсивности поля в образце фотонного кристалла  при заданных параметрах системы.

Программа написана в пакете научных программ для численного моделирования SciLab. Этот свободно распространяемый пакет описан в Википедии: http://ru.wikipedia.org/wiki/Scilab