где ![]() – сила Лоренца,
действующая со стороны электромагнитного поля на распределение зарядов и токов;
– сила Лоренца,
действующая со стороны электромагнитного поля на распределение зарядов и токов;
![]() – плотность импульса электромагнитного
поля;
– плотность импульса электромагнитного
поля; ![]() – максвелловский тензор напряжений.
В области, свободной от источников заряда, скорость изменения плотности
импульса поля равна силе, действующей на рассматриваемую область и определяемой
максвелловским тензором напряжений.
– максвелловский тензор напряжений.
В области, свободной от источников заряда, скорость изменения плотности
импульса поля равна силе, действующей на рассматриваемую область и определяемой
максвелловским тензором напряжений.
Выражения (2.33) и (2.34) лекций дают приближенное описание лазерного
импульса. В среде без дисперсии эти выражения становятся точными. Если
распределение по волновым числам ![]() известно, то,
вычисляя интеграл в (2.33), можно получить огибающую
известно, то,
вычисляя интеграл в (2.33), можно получить огибающую ![]() .
Найдите огибающую
.
Найдите огибающую ![]() , изобразите графически
зависимости
, изобразите графически
зависимости ![]() и
и ![]() ,
определите стандартные отклонения
,
определите стандартные отклонения ![]() и
и ![]() от средних и убедитесь в выполнении
соотношения неопределенностей Гейзенберга
от средних и убедитесь в выполнении
соотношения неопределенностей Гейзенберга ![]() для
каждого из приведенных ниже распределений А (к):
для
каждого из приведенных ниже распределений А (к):
а) ![]() . Это спектральное распределение
соответствует гауссову импульсу и представляет собой минимальный волновой пакет,
т.е.
. Это спектральное распределение
соответствует гауссову импульсу и представляет собой минимальный волновой пакет,
т.е. ![]() ;
;
б) ![]() . Это спектральное распределение соответствует
импульсу с лоренцевой формой;
. Это спектральное распределение соответствует
импульсу с лоренцевой формой;
в) ![]() . Это спектральное распределение отвечает
прямоугольному импульсу.
. Это спектральное распределение отвечает
прямоугольному импульсу.
Одномерный лазерный импульс имеет центральную частоту ![]() и соответствующее волновое число
и соответствующее волновое число ![]() . Огибающая
. Огибающая ![]() для электрического поля
определяется следующим образом:
для электрического поля
определяется следующим образом:
![]() .
.
Найдите огибающую для магнитного поля Нy и вычислите вектор Пойнтинга.
Дисперсия некоторого вещества описывается следующей зависимостью показателя преломления от частоты:
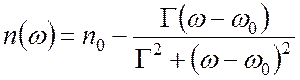 .
.
Найдите групповую скорость ![]() импульса,
распространяющегося в этой среде.
импульса,
распространяющегося в этой среде.
Если в разложении (2.32) частоты ![]() в
окрестности
в
окрестности ![]() можно пренебречь
членами второго и высшего порядков, то огибающая лазерного импульса сохраняет
свою форму. Рассмотрите случай, когда член второго порядка не является малым и
его необходимо учитывать, в то время как членами высшего порядка можно
пренебречь:
можно пренебречь
членами второго и высшего порядков, то огибающая лазерного импульса сохраняет
свою форму. Рассмотрите случай, когда член второго порядка не является малым и
его необходимо учитывать, в то время как членами высшего порядка можно
пренебречь:
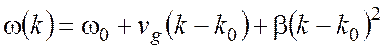 ,
,
где ![]() – групповая
скорость,
– групповая
скорость, ![]() . Найдите огибающую импульса со
спектральным распределением, соответствующим гауссову импульсу
. Найдите огибающую импульса со
спектральным распределением, соответствующим гауссову импульсу
![]()
и определите зависимость ширины огибающей от времени. При расчетах можно использовать следующий интеграл:
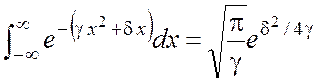 .
.
В этом интеграле вещественная часть параметра ![]() должна быть положительной.
должна быть положительной.
Пусть зависимость показателя преломления от длины волны излучения известна. Покажите, что групповую скорость, описываемую выражением (2.38) лекций, можно вычислить по формуле
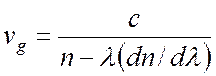 .
.
Покажите, что коэффициент
разложения в ряд Тейлора 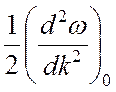 пропорционален дисперсии групповой скорости
и что
пропорционален дисперсии групповой скорости
и что
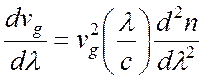 .
.
Пусть ![]() и
и ![]() являются решениями уравнений
Максвелла.
являются решениями уравнений
Максвелла.
а) Покажите, что уравнениям Максвелла удовлетворяют также комплексно-сопряженные величины ![]() и
и
![]() .
Заметим, что
.
Заметим, что ![]() ,
, ![]() и
и ![]() ,
,
![]() отвечают одному и тому же полю, поскольку физический смысл имеют лишь
вещественные части этих величин.
отвечают одному и тому же полю, поскольку физический смысл имеют лишь
вещественные части этих величин.
б) Покажите, что комплексно-сопряженные волновые поля
![]() ,
, ![]()
также удовлетворяют
волновому уравнению, при условии, что среда не имеет потерь (т. е. ![]() и
и ![]() являются
тензорами с вещественными элементами).
являются
тензорами с вещественными элементами).
Исследовать «расплывание» одномерного волнового пакета в диспергирующей
среде. Для этого выбрать амплитудную функцию в виде кривой Гаусса ![]() и учесть квадратичный член в
разложении частоты
и учесть квадратичный член в
разложении частоты ![]() по
по ![]() .
.
Найти фазовую ![]() и групповую
и групповую ![]() скорости распространения импульса
света в среде, диэлектрическая проницаемость которой
скорости распространения импульса
света в среде, диэлектрическая проницаемость которой
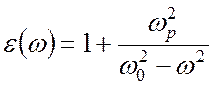 .
.
Ограничиться рассмотрением только случаев больших и малых
(по сравнению с ![]() ) частот
) частот ![]() (
(![]() ).
).
Выведите уравнение (3.4) лекций, которое описывает эллиптически поляризованную волну.
Получите соотношения (3.7) и (3.8) лекций, определяющие длины главных осей эллипса при эллиптической поляризации волны.
Покажите, что конец вектора электрического поля эллиптически поляризованного
света при ![]() будет вращаться по часовой стрелке,
а при
будет вращаться по часовой стрелке,
а при ![]() – против часовой стрелки.
– против часовой стрелки.
Найдите состояние поляризации, которое ортогонально состоянию поляризации
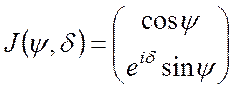 .
.
Ответ: 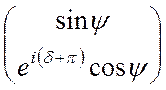 .
.
Покажите, что главные оси эллипсов двух состояний с взаимно ортогональными поляризациями перпендикулярны друг другу, а направления вращения противоположны.
Выведите соотношения (3.12) и (3.13) лекций, определяющие связь параметров эллипса с его комплексным параметром.
Пусть имеются две монохроматические плоские волны вида
![]() ,
,
![]()
Поляризации этих двух волн взаимно ортогональны, т. е.
![]() .
.
а) Предполагая, что ![]() и
и
![]() – фазовые углы, определяемые выражениями
(3.2), покажите, что
– фазовые углы, определяемые выражениями
(3.2), покажите, что ![]() .
.
б) Покажите, что, поскольку углы ![]() и
и ![]() заключены
в интервале
заключены
в интервале ![]() , имеет место неравенство
, имеет место неравенство ![]() .
.
в) Пусть ![]() и
и ![]() – комплексные
параметры, задающие состояния поляризации этих двух волн. Покажите, что
– комплексные
параметры, задающие состояния поляризации этих двух волн. Покажите, что ![]() .
.
г) Докажите, что главные оси эллипсов поляризации взаимно ортогональны, а их эллиптичности имеют одинаковые значения, но противоположные знаки.
Определить характеристики волны, получаемой в результате суперпозиции
двух волн с одинаковой амплитудой, поляризованных по правому и левому кругу,
если в начальный момент разность фаз волн равна ![]() .
.
Пусть электромагнитное излучение распространяется в одномерной периодической среде с диэлектрической проницаемостью
![]() ,
,
причем ось z совпадает с направлением распространения электромагнитной волны.
а) Покажите, что конструктивная интерференция при отражении света имеет место, когда выполняется условие Брэгга
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.