Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 11

Используя полученные соотношения (8), находим коэффициент отражения электромагнитных волн от плоскопараллельной пластины, как отношение квадрата модуля амплитуды отраженной от пластины волны к квадрату модуля амплитуды падающей волны:

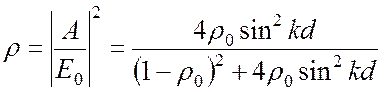                                     .         (9)

Исследование на экстремум функции  показывает, что отражение от пластины равно нулю, если

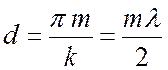                                                    ,                       (10)

где  – целое,  – длина световой волны в пластине.

Задача 1.2.17

Определить характеристики волны, получаемой в результате суперпозиции двух волн с одинаковой амплитудой, поляризованных по правому и левому кругу, если в начальный момент разность фаз волн равна .

Решение

Известно, что электромагнитная волна с любой поляризацией может быть представлена в виде суперпозиции двух линейно поляризованных волн, плоскости колебаний электрического вектора которых взаимно перпендикулярны. Поэтому можно сказать, что электромагнитные волны обладают двумя независимыми состояниями поляризации.

Рассмотрим два взаимно перпендикулярных электрических колебания, совершающихся вдоль осей  и  и отличающихся по фазе на .

                               , .    (1)

Результирующая напряженность  является векторной суммой напряженностей  и  (рис. 1)

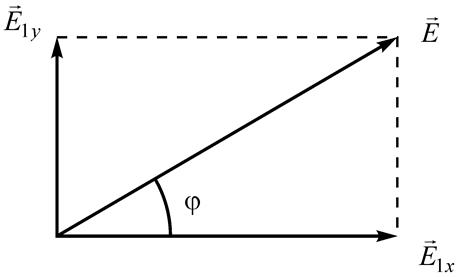
Рис. 1

Угол  между направлениями векторов  и  определяется выражением

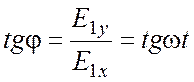                                                   ,                       (2)

следовательно

                                                           .                               (3)

Отсюда вытекает, что конец вектора  движется по окружности против часовой стрелки, то есть результирующая волна является левополяризованной. Уравнение окружности, описываемой концом вектора электрического поля во времени, можно получить, если из уравнения (1) исключить  (см. формулу (3.4) лекции 3). Напряженности волны, поляризованной по правому кругу и сдвинутой по фазе по сравнению с левополяризованной волной, записываются в виде

                           , .                                                               (4)

Удобно произвести сложение описываемых формулами (1), (4) колебаний, представив их в виде комплексных векторов (см. лекцию 3)

                       , .                                                               (5)

Очевидно, что вещественная и мнимая части векторов ,  определяют соответственно ,  и , . Результат сложения комплексных векторов дается формулой

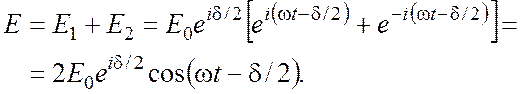                            (6)

Поэтому

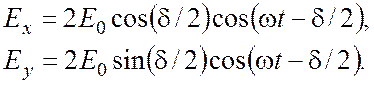                                                 (7)

Из (7) следует, что , т.е. результирующая волна является линейно поляризованной, причем линия колебаний вектора  образует с осью  угол . Если , то линия колебаний совпадает с осью  (рис. 2)

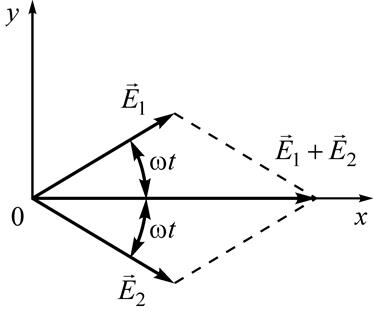
Рис. 2. Образование линейно поляризованной волны в результате сложения циркулярно поляризованных волн.

Задача 2.5.5

Показать, что существуют такие решения уравнений Максвелла, которые соответствуют распространению поверхностных волн Н-типа только вдоль границы раздела между двумя немагнитными сферами с экспоненциальным затуханием по мере удаления от границы раздела между двумя немагнитными сферами с экспоненциальным затуханием по мере удаления от границы раздела. Определить связь между частотой и волновым вектором поверхностной волны, а также характер ее поляризации.

Решение

Пусть граница раздела  совпадает с плоскостью  и волна распространяется вдоль оси , а магнитное поле в волне направлено по оси . Предположим, что в области положительных  диэлектрическая проницаемость равна , а в области отрицательных  диэлектрическая проницаемость равна  (рис. 1).

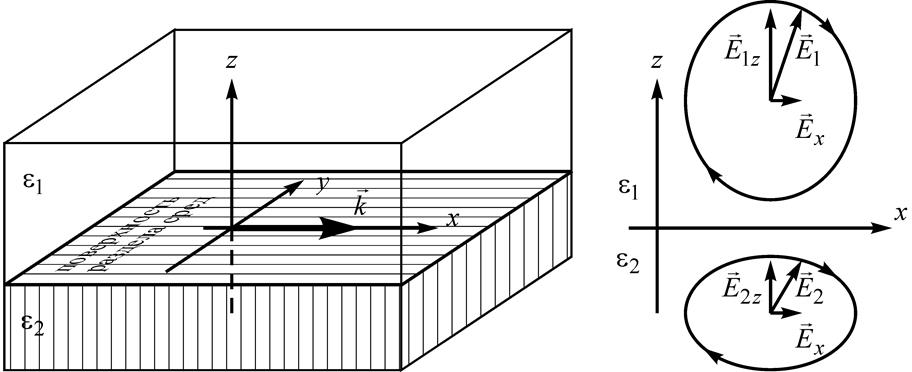
                               (а)                                                                   (б)

Рис. 1. Схема формирования поверхностной электромагнитной волны: а) система координат для плоской поверхности; б) диаграмма вращения вектора электрического поля в средах 1 и 2.

Мы хотим найти условия существования волн, электрическое и магнитное поле которых гармоническим изменяется вдоль границы и во времени и экспоненциально спадает по обе стороны от границы:

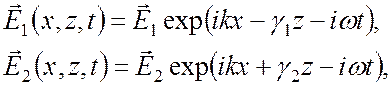                                              (1)

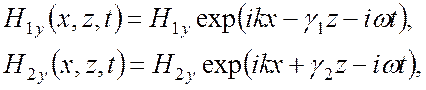                                         (2)

где . Волновой вектор  одинаков в обеих средах, в соответствии с граничными условиями – непрерывностью тангенциальных компонент электрического и магнитного поля при . В первой среде должны выполняться уравнения  и . Для выбранной зависимости полей от координат и времени, уравнение для магнитного поля выполняется тождественно, а первое уравнение имеет вид

                                                .                    (3)

Аналогичному уравнению должно удовлетворять и поле во второй среде:

                                               .                    (4)

Вычитая уравнение (4) из уравнения (3) при условии, что  и , получаем:

                                         .             (5)

Как показано во второй лекции, граничные условия на поверхности раздела двух сред имеют вид

                                                         ,                             (6)

                                                     .                         (7)

Из (5), после подстановки в него граничных условий (6), (7) следует, что

                                                                                  (8)

Из-за положительности  и  при этом следует, что

                                                          ,                              (9)

то есть для существования поверхностной волны необходимо, чтобы диэлектрические проницаемости сред имели разные знаки. Поля в первой и второй средах должны удовлетворять уравнениям

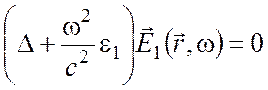                                             ,                (10)

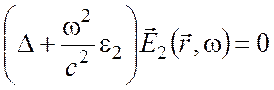                                             .               (11)

Подстановка в (10), (11) полей в виде (1) дает:

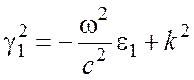                                                   ,                     (12)

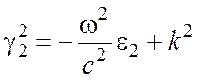                                                  .                     (13)

Найдем теперь закон дисперсии поверхностных волн, то есть, связь  и . Возводя в квадрат равенство (8) и используя выражения (12), (13) получим

                                      ,

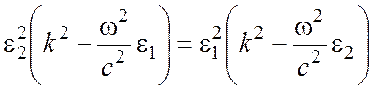или