2. Устный опрос студентов по материалу лекций №№ 15 и 16.
3. Решение задач 3.7.1, 3.7.3 о нахождении плотности фотонных состояний и зонной структуры спектра для волн в двумерном фотонном кристалле. Метод получения точного выражения для плотности фотонных состояний плоскослоистой среды. Исследование роли спонтанной эмиссии в сверхрешетках с фотонной запрещенной зоной.
4. Решение задач 3.7.5, 3.7.6 о нелинейных эффектах в фотонно-кристаллических средах, фотонных запрещенных зонах, оптическом переключении, оптическом диоде.
Домашнее задание:
1. Решение задач №№ 3.7.2 а, б, 3.7.7.
2. Теоретическая подготовка по материалу лекций № 17.
Тема занятия:
Самособирающиеся фотонные холестерические жидкие кристаллы с дефектами решетки.
Содержание занятия:
1. Краткий анализ результатов выполнения студентами домашнего задания по теме предыдущего занятия.
2. Устный опрос студентов по материалу лекции № 17.
3. Решение задачи 3.8.3 а, б, в, г об индуцируемых локальным изменением шага спирали фотонных дефектных модах в холестерическом жидком кристалле.
В отличие от аудиторной работы, которая всегда коллективна, самостоятельная работа является строго индивидуальной. В ней особенно четко проявляются личные качества студента (дисциплинированность, настойчивость, внимательность, наблюдательность, вдумчивость и т.д.), а также его навыки и умения (работать с книгой, сосредотачиваться, логически рассуждать, излагать свои мысли, владеть пером и грамотой письма и т.д.). Отдавая должное обоим видам работ, авторы все же считают самостоятельную работу более важной составляющей учебного процесса. Еще древние говорили, что научить нельзя, можно только научиться.
В данном случае этот вид работы фактически состоит из двух частей.
1. Первая включает в себя выполнение домашнего задания и подготовку к очередному аудиторному занятию.
Выполнение домашнего задания следует начинать с теоретической подготовки, которая включает в себя проработку лекционного материала. Авторы настоятельно рекомендуют не ограничиваться только этим, а прорабатывать еще литературу, которая рекомендована лектором, а также ту, что приведена в конце данной работы. Во-первых, этим у студента вырабатывается умение работать с книгой, а во-вторых, в лекциях невозможно раскрыть материал во всей полноте; лекции дают лишь «скелет» дисциплины, который еще надо снабдить «мышцами», роль которых и играет работа с дополнительной литературой. Все это расширяет профессиональный кругозор будущего бакалавра или специалиста, прибавляя ему уверенности в себе.
После теоретической подготовки следует переходить к решению задач. Авторы рекомендуют начинать эту процедуру с разбора решений аналогичных задач, приведенных в данной работе (см. раздел 4). Сам же процесс решения следует разделить на несколько этапов (авторы рекомендуют пять). На первом из них надо внимательно прочесть текст задачи, как можно глубже вникнуть в ее условие и понять, что требуется определить. На втором этапе это понимание надо изобразить в виде эскиза или рисунка, который при грамотном исполнении помогает еще глубже вникнуть в суть задачи. Иногда хороший рисунок может даже подсказать пути подхода к ее решению. На третьем этапе определяются те законы, которыми эта задача может быть описана, и составляются соответствующие уравнения. Здесь же выясняется, достаточно ли этих уравнений для получения однозначного решения. Если нет, то система уравнений дополняется. Четвертый этап состоит в математическом решении задачи. На пятом необходимо проверить правильность размерности полученных в решении величин и их физическую корректность (например, если требовалось определить энергию светового импульса, то она уж никак не должна быть меньше энергии одного фотона!). Добавим сюда общую рекомендацию: при письменном оформлении домашней работы поясняйте свои действия словами и объясняйте, почему для решения задачи были выбраны именно эти уравнения, а не другие, указывайте область их действия и т.д. Следите за письменной грамотой и стилем изложения. Помните, кто ясно мыслит, тот ясно излагает.
Домашние работы сдаются на проверку преподавателю, который их оценивает и заносит оценку в свой журнал.
2. Вторая часть самостоятельной работы заключается в выполнении задания, которое выдается студентам уже в начале изучения дисциплины. Оно состоит из трех задач, которые необходимо решить в течение всего семестра по мере освоения соответствующего материала, т.к. темы задач относятся к различным ее разделам. Результаты этой работы сдаются преподавателю в письменной форме в три срока, время которых указано в графике учебного процесса и самостоятельной работы студентов. После ее проверки работа может быть возвращена студенту на доработку, если в ней были обнаружены какие-либо недочеты. Методика решения этих шести задач такая же, как изложенная выше.
3. Контроль знаний студента, приобретенных им в процессе практических занятий, осуществляется в виде экзамена. Для получения допуска к экзамену они должны:
· регулярно и с положительными оценками выполнить не менее 60% домашних заданий;
· в срок сдать решения выданных ему в начале семестра шести задач;
· активно участвовать в аудиторных практических занятиях (у доски и при устных опросах теоретического материала).
Используя уравнения Максвелла, выведите уравнение непрерывности для сохранения заряда
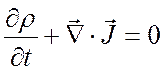 ,
,
где ![]() – плотность заряда, а
– плотность заряда, а ![]() – плотность тока.
– плотность тока.
Применяя теорему Гаусса-Остроградского к уравнениям Максвелла,
найдите граничные условия для нормальных составляющих электрической ![]() и магнитной
и магнитной ![]() индукций
(выражение (1.11) лекций).
индукций
(выражение (1.11) лекций).
Применяя теорему Стокса к уравнениям Максвелла, найдите граничные
условия для тангенциальных составляющих напряженностей электрического ![]() и магнитного
и магнитного ![]() полей
(выражения (1.14) лекций).
полей
(выражения (1.14) лекций).
Выведите гидродинамическое уравнение
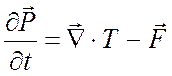 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.