Числовые ряды. Сходимость ряда. Сумма ряда, страница 7

Частный случай: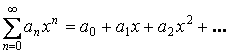

Теорема Авеля. У каждого степенного ряда существует радиус сходимости.

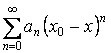, при

 – сходится

 – расходится.

 – точка сходимости.

Если , то , т.е.  – мажорируемый.

Область сходимости:

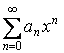 – сходится при

Пример:

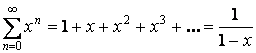  – сходится при .

Теорема. Радиус сходимости  определяется как  .

Доказательство:

Возьмем , тогда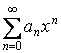

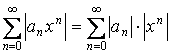
По признаку Даламбера:

 

Отсюда 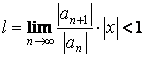 или

Внутри радиуса сходимости степенной ряд мажорируем, его сумма непрерывна, его можно почленно интегрировать и дифференцировать.

Пример:

1) 

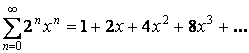
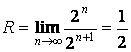 или при  ряд сходится.

2) 

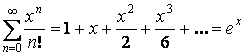
 , значит ряд сходится при любых