Числовые ряды. Сходимость ряда. Сумма ряда, страница 3

Пример:

Ряд –

 и

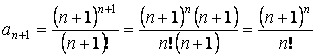
 – ряд расходится.

6.  Радикальный признак Коши:

, при , .

Тогда  если , то ряд сходится, если – ряд расходится.

Доказательство:

1)  Пусть  и  

Тогда, начиная с некоторого , , выполняется неравенство  или .

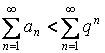
– сходится (бесконечно убывающая геометрическая прогрессия), а значит –сходится по принципу сравнения.

2)  Пусть  и  

Тогда, начиная с некоторого , , выполняется неравенство  или .

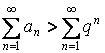
Получаем, что –расходится.