Интеграл Фурье.
Пусть функция ![]() определена
на всей числовой оси и абсолютно интегрируема.
определена
на всей числовой оси и абсолютно интегрируема. 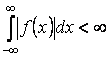
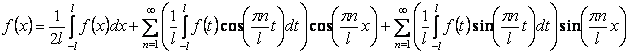 где
где
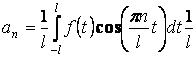 и
и 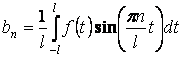
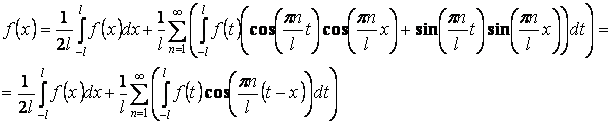
Пусть ![]() ,
тогда
,
тогда 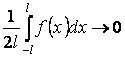
![]() и
и
![]()
 ,
где
,
где
![]() –
интегральная сумма.
–
интегральная сумма.
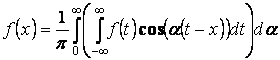 ,
где
,
где
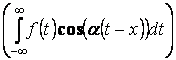 –
интеграл Фурье для
–
интеграл Фурье для ![]() .
.
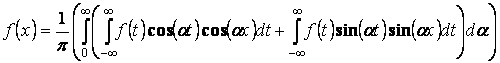
1) Если ![]() – четная, тогда
– четная, тогда
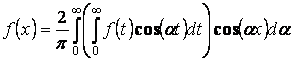
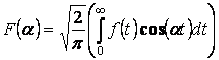 –
косинус преобразования Фурье для
–
косинус преобразования Фурье для ![]() .
.
Отсюда
получаем 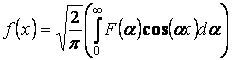
2) Если ![]() – нечетная, тогда
– нечетная, тогда
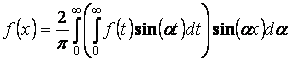
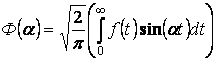 –
синус преобразования Фурье для
–
синус преобразования Фурье для ![]() .
.
Отсюда получаем 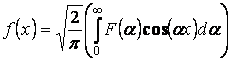 .
.
Интеграл Фурье в комплексной форме.
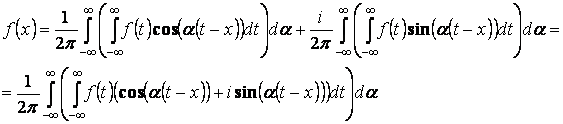
Отсюда 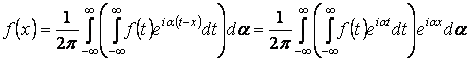 , где
, где
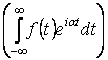 –
–
![]() -спектральная плоскость
-спектральная плоскость ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.