Числовые ряды. Сходимость ряда. Сумма ряда, страница 6

 – сходится и ,  – непрерывна на .

Тогда  – непрерывна на .

Доказательство:

 (из определения непрерывности)

,

где .

При  и  .

Отсюда

Пример:

 на

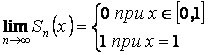 , разрыв при

Теорема. О почленном интегрировании ряда.

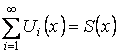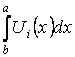Пусть  на  – мажорируемый,  – интегрируемы на  ( – существует). Тогда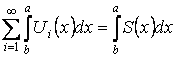

Теорема. О почленном дифференцировании ряда.

Пусть 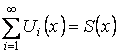 на  – мажорируемый,  – дифференцируемы на  (– существует). Тогда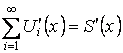

Степенные ряды.

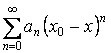, где  – коэффициент,  – произвольная точка, .